2. Department of Physical and Environmental Sciences, University of Toronto at Scarborough, 1265 Military Trail, Toronto, Ontario, Canada
The classic Stefan problem (after J. Stefan, 1835~1893) aims to describe the temperature distribution in a medium undergoing a moisture phase change (Vuik, 1993). It assumes there is a phase interface that can move with time. Many methods have been implemented to determine the freezing–thawing penetration depth in a medium based on this theory, especially where little site-specific information is available (Nelson et al., 1997 ; Woo et al., 2004 ). During the last several decades, the Stefan equation has been widely used in permafrost research for spatial active-layer characterization, using estimated soil properties, air-temperature records, and measured active-layer data obtained from representative locations (Riseborough et al., 2008 ; Wang et al., 2009 ).
The original Stefan equation was derived for only a homogeneous medium, although the small number of parameters contained in the equation makes it possible for extension to a multilayered system (Xie and Gough, 2013). Some algorithms have been developed for use in a multilayered system, such as the JL-algorithm (Jumikis, 1977; Lunardini, 1981) and the algorithm developed by Nixon and McRoberts (1973) (abbreviated as NM-algorithm in this paper). The JL-algorithm was developed by Aldrich (1956) and was used in a multilayered system to simulate the frost penetration below highway and airfield pavements as early as 1956 by Holden et al. (1981) . Xie and Gough (2013) abbreviated it as the JL-algorithm because the mathematical derivation was introduced in detail by Jumikis (1977) and Lunardini (1981). It has been widely used in engineering applications and permafrost research and has been incorporated into some hydrological (Fox, 1992) and land-surface models (Nelson and Outcalt, 1987; Fox, 1992; Woo et al., 2004 ; Yi et al., 2007, 2009 ). By examining the mathematical formulations of the JL-algorithm, Xie and Gough (2013) concluded that the JL-algorithm was not a correct algorithm because it was derived using a flawed mathematical method. Xie and Gough (2013) presented the XG-algorithm and asserted that it is the correct way to apply the Stefan equation to the calculation of the freezing (or thawing) depth in a multilayered soil. Recently, Kurylyk (2015) questioned the XG-algorithm and concluded that the development of the XG-algorithm was premised on mathematical formulations that are not physically tenable. He suggested the NM-algorithm, which was developed by Nixon and McRoberts (1973) and Kurylyk (2015) provided a complete mathematical derivation, is a preferable one. Although the Stefan equation was derived more than 100 years ago, we do not have a unified understanding of its use in a multilayered system.
Upon careful consideration of the mathematical derivation methods of the original Stefan equation and the NM-algorithm, we are asserting that the NM-algorithm was also based on an incorrect assumption because it fails to recognize that the thawing depth in a multilayered soil is a piecewise function and not a continuous function of time. Our work concludes that both the JL-algorithm and the NM-algorithm are not useful extensions of the Stefan equation because both of them were derived using an incorrect assumption. This paper also concludes that the XG-algorithm is a correct and rigorous method to determine the freezing–thawing fronts in multilayered soil, just as the classic Stefan equation does in a homogenous soil.
2 The Stefan equationThe original Stefan problem examined the formation of ice in polar seas. Stefan (1891) assumed that the transport of heat through the ice is rapid, and the temperature in the ice has a linear profile (Jumikis, 1977). At the air–ice interface, the temperature is below the freezing temperature; whereas at the ice–water interface, it is equal to the freezing temperature of water. For a given period, if an amount of seawater changes to ice, the total heat released in this process by this seawater is equal to that is removed through the ice above. This leads to the following differential equation:
| $k\frac{{{\rm d}T_{\textit z}}}{{{\rm d}{\textit z}}} = L\frac{{{\rm d}\xi }}{{{\rm d}t}}$ | (1) |
| $\begin{array}{l}{T_{\textit z}}\left| {_{{\textit z} = 0} = {T_s}} \right.;\\{T_{\textit z}}\left| {_{{\textit z} = \xi } = {T_f}} \right. = 0 \,\, ^\circ {\rm C};\end{array}$ |
And the penetration frost depth given by the Stefan equation:
| $\xi = \sqrt {\frac{{2k({T_s} - {T_f})t}}{L}} = \sqrt {\frac{{2kI}}{L}} $ | (2) |
where k is the thermal conductivity of the ice (W/(m·°C)), Ts is the surface temperature at a given time (°C), Tf is the freezing temperature (°C), z is the thickness the ice (m), ξ is the freezing–thawing depth (m), L is the latent heat of fusion of bulk water (3.35×105 J/kg), and t is the time. I is the total surface thawing index (°C·s).
In the early 1940s, Berggren (1943) (referenced by Holden et al., 1981 ) successfully applied the Stefan equation to the freezing of water in a porous material (soil); and the form of the original Stefan equation was changed to the following:
| $\xi = \sqrt {\frac{{2kI}}{{L\omega \rho }}} $ | (3) |
In Equation (3), L, the latent heat of fusion of bulk water (3.35×105 J/kg) in Equation (2), is replaced by the latent heat of fusion of soil, which is determined by the water content, ω, and the dry bulk density of the soil, ρ (kg/m3).
It can be seen that the original Stefan equation is derived assuming a linear temperature profile. This assumption in ice or in a soil with a small Stefan number (the ratio of sensible heat to latent heat) is reasonable because the specific-heat capacity of ice is much smaller than the latent heat. In fact, under the assumption that the temperature distribution retains a linear profile at any time, temperature at each point is a function of both position and time as the penetration frost is moving downward in the profile, which means the temperature distribution and heat conduction in ice are assumed under a quasi-steady state, not a steady state, and the thermal gradient is not assumed to be constant.
For a more general temperature profile, the Stefan problem can be addressed by solving the one-dimensional heat-conduction equation:
| $k\frac{{{{\rm d}^2}T}}{{{\rm d}{{\textit z}^2}}} = L\frac{{{\rm d}T}}{{{\rm d}t}}$ | (4) |
For this more general problem, the temperature in the ice still has a linear profile, while temperature in the unfrozen section has a general (nonlinear) profile. Newman (1890, referenced by Jumukis, 1977) and Stefan (1891) solved this equation through imposing the initial temperature distribution on the whole medium and a particular boundary condition. However, both Newman and Stefan did not give an explicit solution to this more general problem. The details of Newman's and Stefan's solution were introduced in other research, such as that by Jumukis (1977) and Lunardini (1981). In engineering calculations and permafrost studies, the original Stefan equation is still widely used to analyze the thaw–freeze problem with a general temperature profile, as there are only small differences between predictions by the Stefan equation and measurements.
Following the theory developed by Neumann (1890, referenced by Jumikis, 1977) and Stefan (1891), the thawing-penetration depth is directly proportional to the square root of time, consistent with the Stefan equation (Jumukis, 1977; Lunardini, 1981). In a homogeneous soil profile, the thawing depth can be considered as a continuous function of time:
| $\xi = m\sqrt t $ | (5) |
In this equation, m is a coefficient determined by the physical properties of the soil. This equation is easily understood because we know that the soil thermal conductivity and volumetric heat capacity are generally determined by soil characteristics and soil-water content. Thus in a multilayered soil, the thawing depth is not a continuous function of time but a piecewise function because the physical parameters of different soil layers, in general, are different (Figure 1):
| $\xi = \left\{ \begin{array}{l}{m_1}\sqrt {{t_1}} = {\xi _1}\\[8pt]{Z_1} + {m_2}{\sqrt t _2} = {Z_1} + {\xi _2}\\[8pt] \cdots \cdots \\[8pt]\sum\limits_{i = n}^{i = 1} {{Z_n}} + {m_{n + 1}}\sqrt {{t_{n + 1}}} = \sum\limits_{i = n}^{i = 1} {{Z_n}} + {\xi _{n + 1}}\end{array} \right.\;\;\;\;\;\left. \begin{array}{l}if\;\xi < {Z_1}\\[8pt]if\;{Z_1} < \xi < {Z_1} + {Z_2}\\[8pt] \cdots \cdots \\[8pt]if\;\sum\limits_{i = n}^{i = 1} {{Z_n}} < \xi < \sum\limits_{i = n}^{i = 1} {{Z_n}} + {Z_{n + 1}}\end{array} \right.$ | (6) |
where Z1, Z2, and Zn are the thickness of the soil layers; t1, t2, and tn+1 are the time needed to thaw the given soil layers; m1, m2, and mn+1 are coefficients determined by physical parameters of the soils; ξ is the total thawing depth, and ξ1, ξ2, and ξn+1 are the thawing depth in the soil layers, separately. ξ2 is equal to ξ−Z1 and t2 is equal to t−t1 when the thawing front is in the second soil layer. It can be seen that the freeze–thaw process in a multilayered soil is more complicated than that in a homogenous soil. A more sophisticated algorithm is thus needed to apply the original Stefan equation in a multilayered soil.
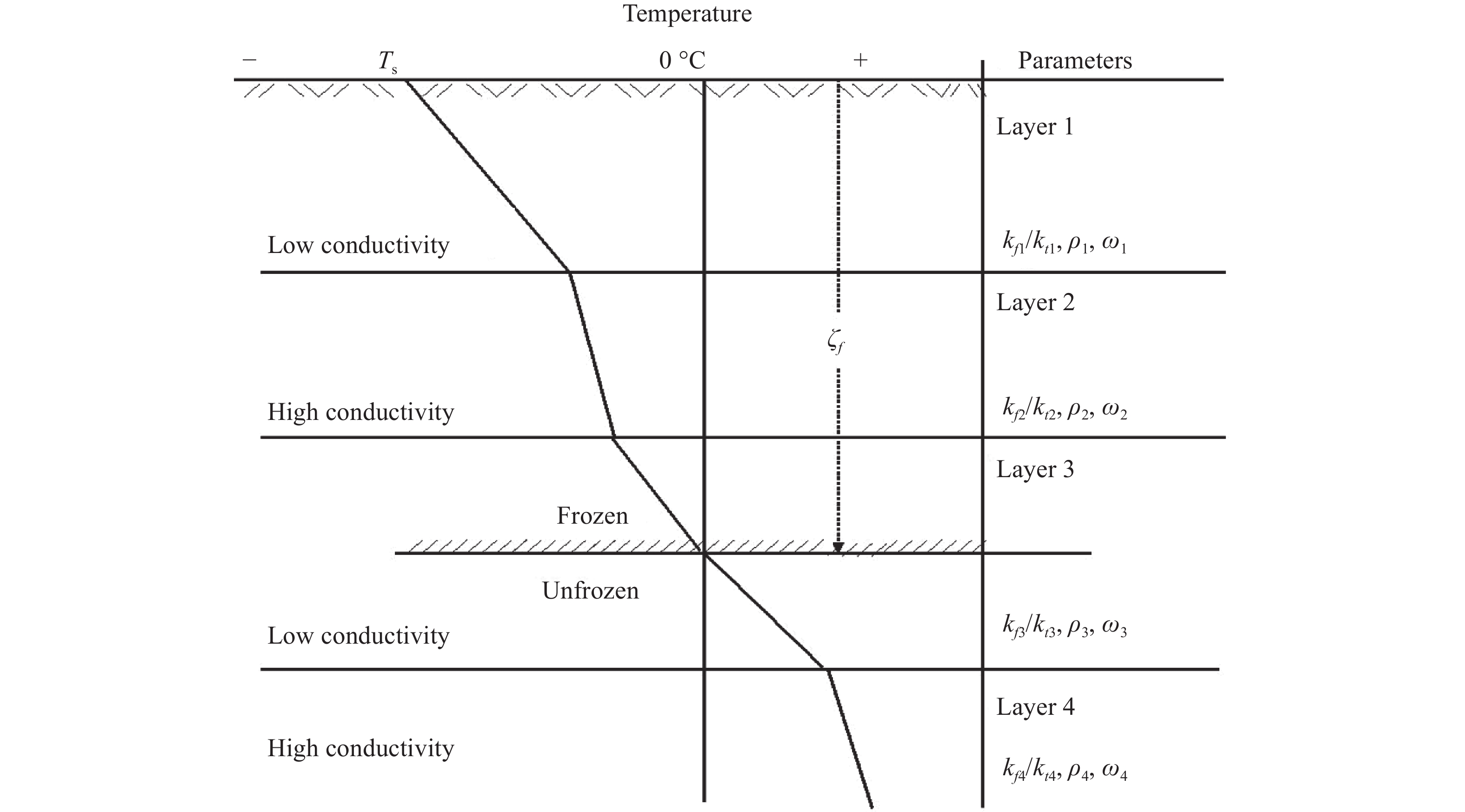
|
Figure 1 Influence of physical parameters on the geothermal gradient (Williams and Smith, 1989) |
In the JL-algorithm, the thawing–freezing depth is calculated by evaluating the partial thawing–freezing index of the total-surface thawing–freezing index that is necessary to thaw–freeze each soil layer. The mathematical derivation of the JL-algorithm was derived based on the differential form of square Stefan equation (Jumikis, 1977):
| $2\xi \Delta \xi = \frac{{2k\Delta I}}{{\rho \omega L}}$ | (7) |
And it considers that ΔI is the partial freezing–thawing index, in degree-days, required to bring about a corresponding partial frost–thaw penetration, Δξ, in any one layer. ΔI is expressed from Equation (7) as follows:
| $\Delta I = ({Q_L}\Delta {\xi })(\frac{{{\xi }}}{{{k}}})$ | (8) |
Then it sets
| ${N_i} = ({Q_{Li}}{{\textit z}_i})(\frac{{{{\textit z}_i}}}{{{k_i}}}) = ({Q_{Li}}{{\textit z}_i})(\frac{{{R_i}}}{2})$ | (9) |
Using this relationship, it obtains a general formula to calculate the partial freezing–thawing index to thaw–freeze for the nth layer, zi=zn units thick:
| ${N_n} = ({Q_{Ln}}{{\textit z}_n})(\sum\limits_{i = 1}^{n - 1} {{R_i} + \frac{{{R_n}}}{2}} )$ | (10) |
where
If the thawing–freezing front is in the (n+1)th layer, from Equation (10), the freezing/thawing depth ξn+1 is calculated from the quadratic equation as follows:
| ${\xi _{n + 1}} = - {k_{n + 1}}{\sum\limits_{i = 1}^n {{R_i} + \left\{ {k_{n + 1}^2{{\left[ {\sum\limits_{i = 1}^n {{R_i}} } \right]}^2} + \left[ {\frac{{2{k_{n + 1}}{N_{n + 1}}}}{{{Q_{Ln + 1}}}}} \right]} \right\}} ^{0.5}}$ | (11) |
The total freezing depth ξ is as follows:
| ${\xi } = \sum\limits_{i = 1}^{i = n} {{{\textit z}_i}} + {\xi _{n + 1}}$ | (12) |
The JL-algorithm has been widely used in engineering applications and permafrost research and was incorporated into some numerical models during last several decades (Nelson and Outcalt, 1987; Fox, 1992; Woo et al., 2004 ; Yi et al., 2007, 2009 ).
3.2 The NM-algorithmNixon and McRoberts (1973) examined some factors affecting the thawing of frozen soil and devised a simple method to calculate the temperature at the layer interface and the thawing depth in a two-layered soil. Kurylyk (2015) introduced this algorithm again and provided the mathematical derivation in detail. Kurylyk (2015) asserted that this methodology is a preferable approach to modify the Stefan equation for two-layered soil and can be expanded to accommodate soils with more than two layers. It was not widely used by researchers although it was introduced in the early 1970s. Because the key equations in both Nixon and McRoberts (1973) and Kurylyk (2015) are the same, we assume the mathematical derivations in both papers are similar; and we will discuss this algorithm using Kurylyk (2015). The following introduction of the mathematical derivation is cited from Kurylyk (2015).
The NM-algorithm was derived from the first principles using heat-transport equations (Kurylyk, 2015). It assumed that when the rate of temperature changes within the subsurface is slow (as in the case of slow downward propagation of the thawing depth), the one-dimensional heat-conduction equation (Equation (4) in this paper) can be approximated with the steady-state heat conduction:
| $k\frac{{{{\rm d}^2}T}}{{{\rm d}{{\textit z}^2}}} = 0$ | (13) |
Kurylyk (2015) believed that this "quasi-steady-state assumption" is valid when the Stefan number is low and latent-energy exchange dominates sensible-energy transfer. And then he deduced that Equation (13) implies the divergence of conductive flux is zero, and the thermal gradient must be a constant for homogenous soil. Kurylyk (2015) assumed that the temperature must be continuous across the interface, as described by the following equation:
| ${T_1}\left| {_{{\textit z} = {Z_1}} = {T_2}} \right.\left| {_{{\textit z} = {Z_1}}} \right.$ | (14) |
T1 and T2 were defined as the temperature distribution in the upper layer and lower layer, respectively. By this relationship, he obtained:
| $- {k_1}\frac{{{\rm d}{T_1}}}{{{\rm d}{\textit z}}}\left| {_{{\textit z} = {Z_1}}} \right. = - {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\textit z}}}\left| {_{{\textit z} = {Z_1}}} \right.$ | (15) |
When the thawing front is in the second layer, the conductive flux above the thawing front is equal to the rate of latent heat absorbed at the thawing front:
| $- {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\textit z}}} = {\omega _2}{\rho _2}L\frac{{{\rm d}\xi }}{{{\rm d}t}}$ | (16) |
And the heat fluxes in the upper and lower layers (but still above the thawing front) are related to the temperatures at the surface, layer interface, and thawing front:
| $- {k_1}\frac{{{\rm d}{T_1}}}{{{\rm d}{\textit z}}} = - {k_1}\frac{{{T_Z} - {T_s}}}{{{Z_1}}}$ | (17) |
| $- {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\textit z}}} = - {k_2}\frac{{{T_f} - {T_{\textit z}}}}{{\xi - {Z_1}}}$ | (18) |
By the conductive-flux continuity condition in the whole layer, an isolated expression for TZ is obtained by combining Equations (17) and (18):
| ${T_z} = \frac{{{k_1}{T_s}}}{{\displaystyle\left(\frac{{{Z_1}{k_2}}}{{\xi - {Z_1}}}\right) + {k_1}}}$ | (19) |
Equation (18) and (19) are combined to provide an expression for the conductive flux above the thawing front:
| $- {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\textit z}}}\left| {_{{\textit z} = {Z_1}}} \right. = \frac{{{k_1}{k_2}{T_s}}}{{{Z_1}{k_2} + {k_1}\xi - {k_1}{Z_1}}}$ | (20) |
This conductive flux is equal to the rate of latent heat absorbed at the thawing front in the second layer:
| $\frac{{{k_1}{k_2}{T_s}}}{{{Z_1}{k_2} + {k_1}\xi - {k_1}{Z_1}}} = {\omega _2}{\rho _2}L\frac{{{\rm d}\xi }}{{{\rm d}t}}$ | (21) |
Rearranging to integrate yields:
| $\frac{{{k_1}{k_2}}}{{{\omega _2}{\rho _2}L}}\int\limits_{t1}^t {{T_s}{\rm d}t = \int\limits_{{Z_1}}^\xi {({Z_1}{k_2} + {k_1}\xi - {k_1}{Z_1}){\rm d}\xi } } $ | (22) |
By integrating the thawing depth based on the time and recalling the fundamental definition of the total thawing index, an expression for the total thawing depth is presented:
| $\xi = \left\{ \begin{array}{l}\displaystyle\sqrt {\frac{{2{k_1}{I_t}}}{{L{\omega _1}\rho _1^{}}}} \qquad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;\;\;{I_t} \le {I_1}\\{\rm{ - }}{{\rm{Z}}_{\rm{1}}}\displaystyle\frac{{{k_2}}}{{{k_1}}} + {Z_1} + \sqrt {\frac{{Z_1^2k_2^2}}{{k_1^2}} + \frac{{2{k_2}{I_t}}}{{L{\omega _2}{\rho _2}}} - \frac{{Z_1^2{k_2}{\omega _1}{\rho _1}}}{{{k_1}{\omega _2}{\rho _2}}}\;\;\;\;\;} \;\;\;\;\;if\;\;{I_t} > {I_1}\end{array} \right\}$ | (23) |
In Equation (23), It refers to the total thawing index. When the total thawing index is less than that used to thaw the first layer, the classic Stefan equation is applied. When the thawing front is in the second layer, the NM-algorithm is used.
3.3 The XG-algorithmThe XG-Algorithm is based on the fact that for a given thaw index, the ratio of the thaw depth calculated by the Stefan equation of two soil types (types A and B; indicated below by a suffix, a or b) in the same locality depends on only the physical parameters of the two soil types, independent of the thaw-index value (Xie and Gough, 2013):
| ${P_{ab}} = \frac{{{\xi _a}}}{{{\xi _b}}} = {\left( {\frac{{2{k_a} \cdot I/(L \cdot {\rho _a} \cdot {\omega _a})}}{{2{k_b} \cdot I/(L \cdot {\rho _b} \cdot {\omega _b})}}} \right)^{0.5}} = {\left( {\frac{{{k_a} \cdot {\rho _b} \cdot {\omega _b}}}{{{k_b} \cdot {\rho _a} \cdot {\omega _a}}}} \right)^{0.5}}$ | (24) |
For a given thaw index, if we know the thawing depth of type A soil, the thawing depth of type B can be deduced:
| ${\xi _b} = \frac{{{\xi _a}}}{{{P_{ab}}}}$ | (25) |
This relationship is derived by reliable mathematical methods and is undoubtedly physically tenable. Hence, in an actual soil profile that is formed by two layers, e.g., layer 1 (thickness z1) and layer 2 (thickness z2), layer 3 (thickness z3), and so on, if we assume that the entire soil column is homogeneous with the same soil physical properties as that of layer 1, for a given value of I, the thawing depth in the virtual soil profile can be calculated by the Stefan equation:
| ${\xi _1} = {(\frac{{2{k_1}I}}{{{\rho _1}{\omega _1}L}})^{0.5}}$ | (26) |
If ξ1≤z1, the thawing front is in layer 1; and the calculation is complete. The real thawing depth is equal to ξ1. If ξ1>z1, which means the thaw index is more than that needed to thaw the actual first layer, then residual depth can be calculated as follows:
| $\Delta {\xi _1} = {\xi _1} - {z_1}$ | (27) |
By Equation (4), it is straight forward to determine the depth of thawed material in the second virtual soil profile by the thaw index that was used to thaw the first type of soil with thickness Δξ1:
| ${\xi _2} = \frac{{\Delta {\xi _1}}}{{{P_{12}}}}$ | (28) |
If ξ2≤z2, the thawing front is in the layer 2; and the calculation is complete. The total thawing depth equals z1+ξ2. If ξ2>z2, the thaw index is more than that required to thaw the sum of layer 1 and layer 2; and thus the thawing front is in the third virtual layer and can be determined by the same method. Through repeating these steps, the thawing depth can be determined. If ξn+1≤zn+1, the sum of the thawing thickness is as follows:
| $\xi = \sum\limits_{i = 1}^{i = n} {({{\rm z}_i}} ) + {\xi _{n + 1}}$ | (29) |
The XG-algorithm is a simple algorithm to determine the freezing–thawing front in a multilayered soil, no matter how thick each layer is or how many layers the soil profile contains. In a two- or three-layered soil, it needs only a few additional steps to calculate the thawing–freezing depth by the Stefan equation (Xie and Gough, 2013).
4 Comments on thaw–freeze algorithms for multilayered soil using the Stefan equation 4.1 The JL-algorithmBy examining the mathematical formulation of the JL-algorithm carefully, Xie and Gough (2013) concluded that the JL-algorithm was incorrect because it was derived using incorrect assumptions. It was based on the continuous differential form of the Stefan equation, while it failed to recognize that the thawing depth in a multilayered soil is a piecewise function of time. Xie and Gough (2013) provided a detailed analysis of this algorithm. In this paper, we further discuss this algorithm by analyzing the differential form of Equation (6):
| ${\rm d}\xi = \left\{ \begin{array}{l}{\rm d}{\xi _1}\\[8pt]{\rm d}{\xi _2}\\[8pt] \cdots \cdots \\[8pt]{\rm d}{\xi _{n + 1}}\end{array} \right.\;\;\;\;\;\left. \begin{array}{l}if\;\xi \le {Z_1}\\[8pt]if\;{Z_1} < \xi < {Z_1} + {Z_2}\\[8pt] \cdots \cdots \\[8pt]if\;\sum\limits_{i = n}^{i = 1} {{Z_i}} < \xi < \sum\limits_{i = n}^{i = 1} {{Z_i}} + {Z_{n + 1}}\end{array} \right.$ | (30) |
Equation (30) shows the differential forms are distinct for the different layers. The relationship given by Equation (7) is correct in only the first layer, and it cannot be extended to the second layer. When the thawing–freezing penetration front is in the second layer, ξ1 remains constant (and is equal to Z1); and the thawing–freezing depth is a function of time, with a coefficient determined by the physical parameters of the second layer. The JL-algorithm used a unified symbol to represent the thawing depth in different soil layers, which is valid in only the first layer; and it cannot be extended to the lower layer(s) because the differential forms of the thawing depth are not same in these layers as in the first layer. Thus, it can be concluded that the JL-algorithm was derived using invalid assumptions, as it was based on the continuous differential form of thawing depth in a multilayered soil.
4.2 The NM-algorithmThe NM-algorithm has also failed to recognize that the thawing depth in a multilayered soil is a piecewise function and not a continuous function of time. We point out this by analyzing the mathematical derivation.
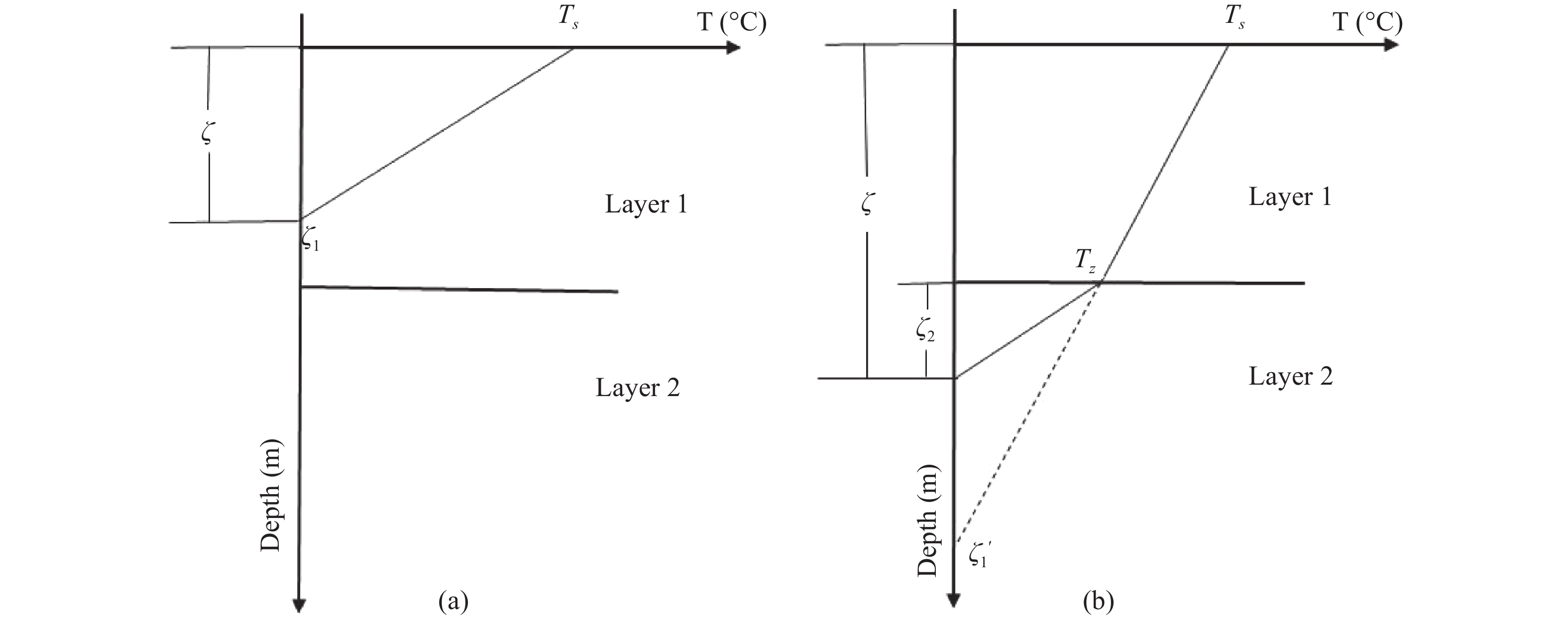
|
Figure 2 Diagrammatic sketch for the thawing/freezing depth in the first layer (a) and the second layer (b) |
In a multilayered soil, when it is very close to the interface, temperatures in the upper layer and the lower layer are approximately equal to the temperature at the interface. However, the thermal gradient in the lower layer is not always equal to that in the upper layer although the temperature profile is assumed to be linear in both the upper layer and the lower layer, respectively (Figure 1). In a multilayered soil, the process of conductive heat flux through the layer interface cannot be described by Equation (15) because the thawing depth in the first layer and the thawing depth in the second layer cannot be represented by same symbol, dz. It should be described as follows:
| $- {k_1}\frac{{{\rm d}{T_1}}}{{{\rm d}\xi _1'}} = - {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\xi _2}}}\left| {_{{\xi _2} = \xi - {Z_1}}} \right.$ | (31) |
Figure 2 graphically illustrates the relationship contained in Equation (31). When the thawing front is in the first layer, ξ1' is equal to ξ1. When the thawing front is in the second layer, ξ1' is a virtual depth that is determined by the thermal gradient in the first layer.
Following the assumptions of the Stefan equation, the conductive heat flux is equal to the total latent heat absorbed at the thawing front in the soil. When the thawing depth is in the first layer, the balance is described as follows:
| $- {k_1}\frac{{{\rm d}{T_1}}}{{{\rm d}{\xi _1}}} = {\omega _1}{\rho _1}L\frac{{{\rm d}{\xi _1}}}{{{\rm d}{t_1}}}$ | (32) |
When the thawing depth is in the second layer, the balance should be described as follows:
| $- {k_2}\frac{{{\rm d}{T_2}}}{{{\rm d}{\xi _2}}}\left| {_{{\xi _2} = \xi - {Z_1}}} \right. = {\omega _2}{\rho _2}L\frac{{{\rm d}{\xi _2}}}{{{\rm d}{t_2}}}$ | (33) |
From Equations (31) to (33), it can be seen that different symbols are needed to represent the total thawing depth, the thawing depth in the first layer, and the thawing depth in the second layer because the thawing depth in a multilayered soil cannot be described by a continuous function of time. If we use the same symbols,
| ${\omega _1}{\rho _1}L\frac{{{\rm d}\xi }}{{{\rm d}t}} = {\omega _2}{\rho _2}L\frac{{{\rm d}\xi }}{{{\rm d}t}}$ | (34) |
This relationship is true only in a homogeneous soil or under the special condition when ω1ρ1 is equal to ω2ρ2, which is a severely limiting constraint for a general multilayered soil. Thus, the NM-algorithm does not correctly represent the interface and is not a reliable method to apply the Stefan equation in a multilayered soil.
The NM-algorithm tried to obtain a simplified solution for the heat-conduction equation when the thawing front is in the lower layer, by integrating temperature at the layer interface, Tz, as done by the original Stefan equation in a homogenous medium. However, this approach ignores a significant fact that the surface temperature remains constant under the assumption of the original Stefan equation, while the temperature at the layer interface is not constrained in this way. Based on the relationship illustrated by Figure 2, an expression for Tz can be provided:
| ${T_z} = \frac{{\xi _1' - {Z_1}}}{{\xi _1'}}{T_s}$ | (35) |
If ξ1' is calculated by the original Stefan equation, Tz can be expressed as a function of time:
| ${T_z} = {T_s} - {Z_1}\sqrt {\frac{{{\omega _1}{\rho _1}L{T_s}}}{{2{k_1}t}}} $ | (36) |
This relationship is independent of the soil characteristics of the lower layer. The mathematical foundation of Equation (36) is the assumption of the original Stefan equation that the temperature in the medium has a linear profile. Equation (36) is suitable for any time when the thawing front is in the lower layer. Figure 3 shows the change trend of the Tz with time.
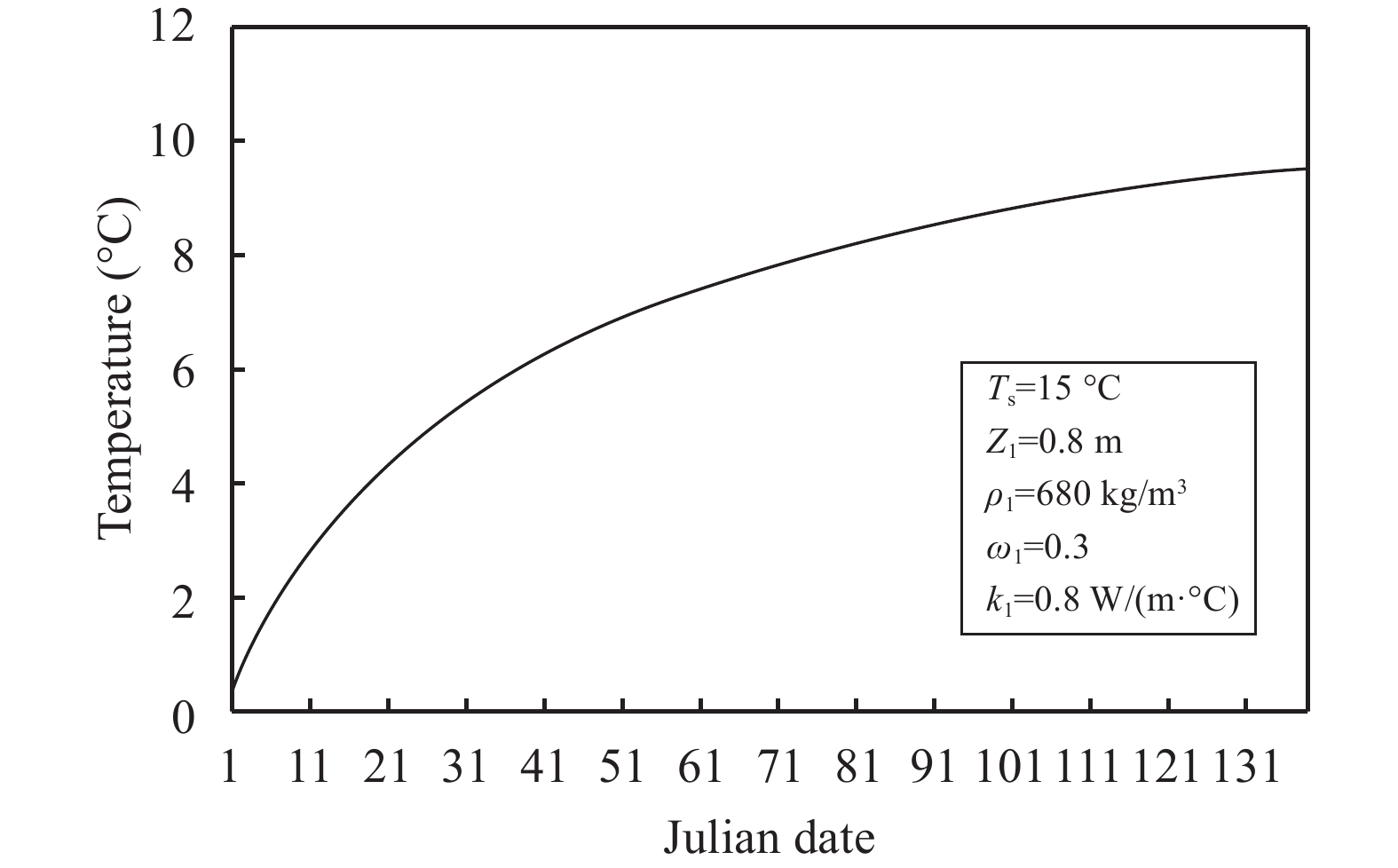
|
Figure 3 The change trend of the temperature at the interface, Tz, with time, based on given parameters |
It is difficult to solve an equation within the framework of one-dimensional heat conduction for the time-dependent surface temperature. Even in Newman's solution and Stefan's solution for a general soil-temperature profile, the surface temperature is assumed to be a constant (Jumikis, 1977; Lunardini, 1981). Nixon and McRoberts (1973) mentioned that an approximate analytical solution was provided by Lock et al. (1969) for power law and sinusoidal variations in the surface temperature. However, the solution suggested in Lock et al. (1969) is considerably more complicated than the original Stefan equation; and the rate of thawing needs to be determined by some other method (Nixon and McRoberts, 1973). Thus, it can be concluded that the NM-algorithm contains some incorrect assumptions and is not a valid way to use the Stefan equation for the thawing process in a multilayered soil.
4.3 The XG-algorithmThe XG-algorithm extends the classic Stefan equation to multiple layers. The theoretical basis of the XG-algorithm is the fact that for a given thaw index, the thawing depth calculated by the Stefan equation for two soil types in the same locality depends on only the physical parameters of the two soil types. This relationship is suitable for the soils at the surface as well as at any depth. The XG-algorithm does not deviate from the fundamental physics of the Stefan equation. However, because it uses a virtual thawing–freezing depth in the upper layer soil to determine the actual thawing depth in the lower-layer soil, some researchers have held its reliability suspect. For example, Kurylyk (2015) has said that the XG-algorithm cannot account for the change of temperature distribution in the soil; and the equipotent thawing–freezing depth, Δξ1, cannot be obtained independently of the lower-layer thermal properties and then directly employed to obtain the thawing depths, ξ2, in the lower layer. This critical assessment gives us an opportunity to demonstrate further the validity of the XG-algorithm.
As illustrated by Figure 2, for a given thermal gradient in the first layer, there is a stretched virtual depth in the lower layer that follows the thermal gradient in the first layer. This virtual depth is a result of assuming that the soil-temperature gradient is a linear profile, as prescribed by the original Stefan equation. Hence, it can be deduced that Δξ1 can be obtained independently of the lower-layer thermal properties. When the thawing front is in the lower layer, the total latent heat absorbed by the lower soil is not only a function of the layer-interface temperature but also a function of time. For a given thawing depth in the lower layer, ξ2, it must correspond to a specific thawing index, I2. We can use the Stefan equation to calculate how much soil thickness can be thawed if the second layer soil is exchanged with the first layer soil:
| $\begin{split}\Delta \xi _1' & = \displaystyle \sqrt {\frac{{2{k_1}{I_2}}}{{L{\omega _1}{\rho _1}}}} = \displaystyle\sqrt {\frac{{2{k_1}\frac{{L{\omega _2}{\rho _2}{\xi _2}}}{{2{k_2}}}}}{{L{\omega _1}{\rho _1}}}} \\[5pt] & = \displaystyle\sqrt {\frac{{{k_1}{\omega _2}{\rho _2}}}{{{k_2}{\omega _1}{\rho _1}}}} {\xi _2} = \displaystyle{P_{12}}{\xi _2} = \Delta {\xi _1}\end{split}$ | (37) |
The calculated result is exactly equal to that calculated by the XG-algorithm. On the contrary, if a given thawing depth, Δξ1, occurs in a homogenous soil, the equivalent thawing–freezing in a different soil, ξ2, can be obtained via the same method. The relationship between the thawing depth and the thawing index given in the Stefan equation ensures that Δξ1 can be obtained independently and employed to obtain ξ2 via the XG-algorithm. The results show clearly that the procedure used by the XG-algorithm is correct.
It has been demonstrated that the mathematical derivation process of the XG-algorithm is simple and perfectly follows the assumptions of the Stefan equation. Unlike the NM-algorithm, it does not analyze the thermal gradient in both upper and lower soil layers. In fact, as was discussed above, it is not a practical way to obtain the thawing depth by performing an integral operation of the temperature at the layer interface. The XG-algorithm uses a flexible way to solve the problem, based on the relationship between the thawing depth and the thaw index given by the Stefan equation. It can be concluded that the XG-algorithm is a rigorous method to determine the freezing–thawing fronts in multilayered soil, just as the classic Stefan equation does in a homogenous soil.
5 Discussion and conclusionFreeze–thaw processes in a soil are complex, as many factors play key roles; and assumptions have to be made by numerical methods to estimate the freezing–thawing penetration depth. The Stefan equation provides a simple relationship between the freezing–thawing index and the freezing–thawing depth, based on the assumption that the latent heat of phase change in the soil layer is much larger than the sensible heat (Jumikis, 1977). It ignores convective heat flow from precipitation, snow melt, and surface water, which (though usually negligible) can be an important factor in soil freezing–thawing (Bonan, 1989). Hence, the simulation results of the Stefan equation always have margin of errors compared to the actual observed values. Those errors caused by the initial physical assumptions may be inevitable, but calculation errors caused by incorrect mathematical methods can be eliminated. It is not a good choice to decide which algorithm is the right one based on the simulation results at some special sites. In Xie and Gough (2013), we compared the simulation results between JL-algorithm and XG-algorithm and discussed some particulars about the difference. In the case of a two-layered thawing soil, simulation results were same for the NM-algorithm and the JL-algorithm although these two approaches were developed using seemingly very different techniques (Kurylyk, 2015). Hence, in this paper, we will not repeat that work; interested readers may refer to those discussions in Xie and Gough (2013).
This paper has discussed the principle of the Stefan equation and some algorithms that apply it to multilayered soils. Based on the mathematical derivation of these algorithms, this work concluded that the JL-algorithm and the NM-algorithm are incorrect because both of them have failed to recognize that the thawing depth in a multilayered soil is a piecewise function and not a continuous function of time. The XG-algorithm was shown to be a more rigorous method to determine the freezing–thawing fronts in multilayered soil, just as the classic Stefan equation does in a homogenous soil.
Acknowledgments:This work was supported by grants from the National Natural Science Foundation of China (41671068, 41421061, and 41771040), the State Key Laboratory of Cryospheric Sciences (SKLCS-ZZ-2017), and the Hundred Talents Program of the Chinese Academy of Sciences granted to ChangWei Xie (51Y551831).
Aldrich HP. 1956. Frost penetration below highway and airfield pavements. Highway Research Board Bulletin, 135: 124-144. |
Berggren WS. 1943. Prediction of temperature distribution in frozen soil. Transactions American Geophysical Union, 24(3): 71-77. |
Bonan GB. 1989. A computer model of the solar radiation, soil moisture, and soil thermal regimes in boreal forests. Ecological Modeling, 45: 275-306. |
Fox JD. 1992. Incorporating freeze-thaw calculations into a water balance model. Water Resource Research, 28: 2229-2244. |
Holden JT, Jones IR, Dudek SJ. 1981. Heat and mass flow associated with a freezing front. Engineering Geology, 18: 153-164. |
Jumikis AR, 1977. Thermal Geotechnics. New Brunswick: Rutgers University Press, pp. 375.
|
Kurylyk BK, 2015. Discussion of: A simple thaw-freeze algorithm for a multi-layered soil using the Stefan equation by Xie and Gough, 2013. Permafrost and Periglacial Processes, 200–206. DOI: 10.1002/ppp.1834.
|
Lunardini VJ, 1981. Heat Transfer in Cold Climates. New York: Van Nostrand Reinhold Publishers, pp. 320–351.
|
Nelson FE, Outcalt SI. 1987. A computational method for prediction and regionalization of permafrost. Arctic and Alpine Research, 19(3): 279-288. |
Nelson FE, Shiklomanov NI, Mueller GR, et al. 1997. Estimating active layer thickness over a large region: Kuparuk River Basin, Alaska, USA. Arctic and Alpine Research, 29(4): 367-378. |
Nixon JF, McRoberts EC. 1973. A study of some factors affecting the thawing of frozen soils. Canadian Geotechnical Journal, 10: 439-452. DOI:10.1139/t73-037 |
Riseborough D, Shiklomanov N, Etzelmuller B, et al. 2008. Recent Advances in Permafrost Modeling. Permafrost and Periglacial Processes, 19: 137-156. DOI:10.1002/ppp.615 |
Vuik C. 1993. Some historical notes on the Stefan problem. South African Journal of Economics, 43(4): 329-335. |
Wang CH, Jin SL, Wu ZY, et al. 2009. Evaluation and Application of the Estimation Methods of Frozen (Thawing) Depth over the China. Advances in Earth Science, 24(2): 132-140. |
Woo MK, Arain MA, Mollinga M, et al. 2004. A two-directional freeze and thaw algorithm for hydrologic and land surface modeling. Geophysical Research Letters, 31: L12501. DOI:10.1029/2004GL019475 |
Xie CW, Gough WA. 2013. A simple thaw-freeze algorithm for a multi-layered soil using the Stefan Equation. Permafrost and Periglacial Processes, 24: 252-260. DOI:10.1002/ppp.1770 |
Yi SH, Mcguire AD, Harden J, et al. 2009. Interactions between soil thermal and hydrological dynamics in the response of Alaska ecosystems to fire disturbance. Journal of Geophysical Research, 114: G02015. DOI:10.1029/2008JG000841 |
Yi SH, Woo MK, Arain MA. 2007. Impacts of peat and vegetation on permafrost degradation under climate warming. Geophysical Research Letters, 34: L16504. DOI:10.1029/2007GL030550 |
 2017, Vol. 9
2017, Vol. 9
