1 Introduction

One of the characteristic features of the modern underground construction is an increase in the depth of deposits and, as a consequence, complication of geotechnical conditions. This circumstance is directly connected with an increase in opening depth of unstable fluid-saturated rocks requiring special building methods. One such method is artificial ground freezing which is used for vertical shaft sinking. Effectiveness of this technique is confirmed by long-term experience of its application in Russia and other countries and is determined by the reliability of the ice wall with calculated thickness. The Verkhnekamsk potash deposit in the Urals, Starobinsk potash deposit in Belorussia and the Gremyachinsk potash deposit in the Volga region were developed with the use of artificial ground freezing method.

Modern development of artificial ground freezing technique is directly related to an increase in freezing depth. In turn, this is connected with economic efficiency issues and problems of guaranteed closure of individual ice bodies to a single wall along with achieving the given strength as soon as possible. Application of this technique was developed in response to the 1990's, with recommendations and analytical techniques for the definition of freezing time, the required thickness of the ice wall, and diameter of the circle of the freezing columns location. The current recommendations and analytical techniques often lead to the two limiting cases: creation of non-tight ice wall and formation of an ice wall with excessive thickness which is not effective from an economic point of view. One of the possible solutions to both problems is direct numerical simulation of the ice wall formation in fluid-saturated rocks under specific hydrogeological conditions.

Solution to the problem of artificial ground freezing with the use of direct numerical simulation depends on two factors: initial data on the thermal and mechanical properties of rocks, and adequacy of the used physical model. Artificial ground freezing is a complex multiphasic phenomenon including closely related thermal, mechanical and hydrodynamic processes. Modern physical models which are used in civil engineering, extractive industry, soil science and agricultural engineering can be divided into the following groups: rigid-ice (Miller, 1978; O'Neill and Miller, 1985; Sheng et al., 1995 ), thermodynamic (Harlan, 1973; Guymon and Luthin, 1974; Jame and Norum, 1980; Konrad, 1994; Noborio et al., 1996a ,b; Hansson et al., 2004 ; Nishimura et al., 2009 ), semi-empirical (Konrad and Morgenstern, 1981; Nixon, 1992) and poromechanical models (Coussy, 2004; Coussy and Monteiro, 2007, 2008). Thermodynamic models can be divided into two classes: freezing models of fully saturated porous media (Mikkola and Hartikainen, 2001; Kruschwitz and Bluhm, 2005) and models which take into account unfrozen water after phase-transition (Rempel et al., 2004 ; Zhou and Meschke, 2013). Despite the fact that later models describes physical processes of individual grains and pores more accurately in order to describe phase transition at large spatial scales, separate investigations are still required of unfrozen water on the phase transition rate and coupled filtration-mechanical processes within porous media upon freezing.

This study is devoted to the development of a coupled thermo-hydro-mechanical model of fluid-saturated poroelastic media under an assumption of the full transition of liquid into ice. This model is used for numerical simulation of artificial ground freezing Starobinsk deposit taking into account available geophysical and physical data.

2 Mathematical formulation of thermo-hydro-mechanical boundary value problem

The object of simulation is layered porous media. In general, this media is a three-phased material consisting of a dry skeleton, fluid and ice that completely fill the pore space. In the initial configuration porous media is completely filled with water. All liquid transforms into ice and dry skeleton remains unchanged during the phase transition process. Developed model is restricted to isotropic linear theory of thermo-poroelasticity within which it is assumed that the media undergoes small deformations, and changes in density and porosity in each phase are small compared with the initial configuration. It is also assumed that the liquid is nearly incompressible.

The complete three-dimensional formulation of the model under the aforementioned assumptions includes the heat Equation (1), Fourier law (2), equilibrium Equation (3), constitutive Equations for the mechanical behavior description (4), geometric relation for linear strain tensor (5), continuity Equation (6), and the Darcy law (7) which can be written in the following form:

$\rho {c_p}\frac{{\partial T}}{{\partial t}} + {\rho _f}{c_{p,f}}\bar v \cdot \bar \nabla T + \bar \nabla \cdot \bar q = 0,$

(1)

$\bar q = - k\bar \nabla T,$

(2)

$\bar \nabla \cdot \tilde \sigma = \rho \bar g,$

(3)

$\tilde{\sigma }=\tilde{\tilde{C}}:\left( \tilde{\varepsilon }-{{{\tilde{\varepsilon }}}_{T}} \right)-{{\alpha }_{B}}{{p}_{f}}\tilde{E},$

(4)

$\tilde \varepsilon = \frac{1}{2}\left[ {\bar \nabla \bar u + {{\left( {\bar \nabla \bar u} \right)}^T}} \right],$

(5)

${\rho _f}S\frac{{\partial {p_f}}}{{\partial t}} + \bar \nabla \cdot \left( {{\rho _f}\bar v} \right) = - {\rho _f}{\alpha _B}\frac{{\partial {\varepsilon _{vol}}}}{{\partial t}},$

(6)

$\bar v = - \frac{{k'}}{\mu }\left( {\bar \nabla {p_f} + {\rho _f}g\bar \nabla z} \right).$

(7)

where ρ is effective density of the system "dry skeleton-liquid-ice" (kg/m³), c_p is effective heat capacity of the system "dry skeleton-liquid-ice" at constant pressure (J/(kg·K)), k is effective thermal conductivity coefficient of the system "dry skeleton-liquid-ice" (W/(m·K)), T is absolute temperature (K), $\bar q$ is heat flux vector (W/m²), t is time (s), ρ_f is fluid density (kg/m³), ${c_{p,f}}$ is specific heat of the fluid (J/(kg·K)), $\tilde \sigma $ is Cauchy stress tensor (Pa), $\bar \nabla $ is Hamiltonian, $\bar g$ is acceleration of gravity (m/s²), C is stiffness tensor (Pa), which has two components in case of the isotropic linear elasticity (K is bulk modulus, G is shear modulus), α_B is Biot coefficient, $\bar v$ is Darcy's velocity (m/s), p_f is pore pressure of fluid (Pa), $\tilde E$ is unity tensor, $\tilde \varepsilon $ is full strain tensor, $\bar u$ is displacement vector (m), ${\tilde \varepsilon _T}$ is thermal strain, ε_vol is volumetric part of the full strain tensor, k' is permeability coefficient (m²), μ is dynamic viscosity of the fluid (Pa·s), z is vertical coordinate (m), S is fluid loss coefficient defined as S = nχ_f+ (α_B − n ) $ (1 - {\alpha _B})/{K_d}$ , where n is porosity, χ_f is fluid compressibility, (Pa⁻¹), and K_d is bulk modulus of the dry skeleton (Pa).

Expressions for density of the considered system taking into account phase transition from state 1 (fluid) to state 2 (ice) and influence of the pore pressure p_f and temperature T have the form:

$\rho = \theta {\rho _{sf}} + (1 - \theta ){\rho _{si}},$

(8)

${\rho _{sf}} = {\rho _f}\left[ {1 + {\alpha _f}(T - {T_0}) + {\chi _f}{p_f}} \right]n + {\rho _s}(1 - n),$

(9)

${\rho _{si}} = {\rho _i}\left[ {1 + {\alpha _i}(T - {T_0}) + {\chi _i}{p_i}} \right]n + {\rho _s}(1 - n),$

(10)

where θ characterizes fraction of fluid phase in the material and (1−θ) is fraction of ice, ρ_s is density of the dry skeleton (kg/m³), χ_i is ice compressibility coefficient (Pa⁻¹), ρ_i is ice density (kg/m³), α_f is thermal expansion coefficient of the fluid (K⁻¹), α_i is thermal expansion coefficient of ice (K⁻¹), χ_i is compressibility coefficient of ice (Pa⁻¹), and T₀ is initial temperature (K).

The following relation was used in order to define effective specific heat at constant pressure:

$\begin{array}{l}{c_p} = \displaystyle \frac{1}{\rho }\left[ {\theta {\rho _{sf}}\left\{ {n{c_{p,f}} + \left( {1 - n} \right){c_{p,s}}} \right\}} \right.\\\quad \quad \left. { + (1 - \theta ){\rho _{si}}\left\{ {n{c_{p,i}} + (1 - n){c_{p,s}}} \right\}} \right] +\displaystyle L\frac{{\partial {\alpha _m}}}{{\partial T}},\end{array}$

(11)

where ${\alpha _m} = \displaystyle \frac{1}{2}\frac{{\left( {1 - \theta } \right){\rho _{si}} - \theta {\rho _{sf}}}}{{\theta {\rho _{sf}} + \left( {1 - \theta } \right){\rho _{si}}}}$ , ${c_{p,s}}$ = specific heat of the dry skeleton (J/(kg·K)), ${c_{p,i}}$ = specific heat of ice (J/(kg·K)), and L = latent heat, (J/kg).

Effective thermal conductivity was defined as:

$k = \theta \left\{ {n{k_f} + (1 - n){k_s}} \right\} + \left( {1 - \theta } \right)\left\{ {n{k_i} + (1 - n){k_s}} \right\},$

(12)

where k_f = thermal conductivity of the fluid (W/(m·K)), k_s = thermal conductivity of the dry skeleton (W/(m·K)), and k_i = thermal conductivity of ice (W/(m·K)).

Influence of the θ on the permeability coefficient k' was taken into account with the use of Heaviside function:

$k'\left( \theta \right) = \left\{ {_{ \displaystyle 0,\theta = 0}^{ \displaystyle k',\theta = 1}} \right.$

(13)

Permeability coefficient k' was estimated by the values of the filtration coefficient k_f' of every layer, obtained during hydrogeological investigations of this rock mass:

$k' = \frac{{{k_f}'\mu }}{{\rho g}},$

(14)

where μ = 10⁻³ = dynamic viscosity of fluid (Pa·s).

Effect of the volumetric strain, pressure and temperature was taken into account as Equation (4):

$n = {n_0} + {\alpha _B}{\varepsilon _{vol}} + \frac{1}{N}{p_f} - 3{\alpha _s}\left( {{\alpha _B} - {n_0}} \right)\left( {T - {T_0}} \right),$

(15)

where N = Biot tangent modulus (Pa), α_s = thermal expansion coefficient of the dry skeleton (K⁻¹), and n₀ = initial porosity.

As it has been mentioned above, every layer is isotropic. Results of laboratory studies of the elastic properties K_si and G_si of water-saturated rock samples under negative temperature were used to define bulk modulus K and shear modulus G of the dry skeleton. Assuming that effective elastic modulus of the frozen rock mass is determined by the mixture rule, elastic modulus of the dry skeleton K and G can be found as

$\begin{array}{l}K = \displaystyle \frac{{{K_{si}} - n{K_i}}}{{1 - n}},\$12pt]G = \displaystyle \frac{{{G_{si}} - n{G_i}}}{{1 - n}},\end{array}$

where K_i = 1.8 × 10⁹ Pa, G_i = 1.4 × 10⁹ Pa, which are bulk modulus and shear modulus of ice. Values of K and G for every considered layer are presented in Table 1.

The Biot coefficient and the Biot tangent modulus were defined as:

$\begin{array}{l}{\alpha _B} = \displaystyle1 - \frac{{{K_d}}}{K}\$12pt] \displaystyle \frac{1}{N} = \frac{{{\alpha _B} - n}}{K}\end{array}$

where K_d is bulk modulus of the dry porous skeleton calculated by the formula:

${K_d} = \frac{K}{{\displaystyle 1 + \frac{{3\left( {1 - \nu } \right)n}}{{2\left( {1 - 2\nu } \right)\left( {1 - n} \right)}}}}$

where $\nu = 9K/2(G + 3K) - 1$ = Poisson's ratio of soil particles.

Thermal strain ${\tilde \varepsilon _T}$ was determined according to the equation:

${\tilde \varepsilon _T} = {\alpha _s}\left( {T - {T_0}} \right)\tilde E$

(16)

Equations (1)~(15) are supplemented with the following initial and boundary conditions:

${p_f}\left( {t = 0} \right) = 0$

(17)

$\bar v\left( {t = 0} \right) = \bar 0$

(18)

$\bar u\left( {t = 0} \right) = \bar 0$

(19)

${T_i}\left( {t = 0} \right) = {T_{{o_i}}},\;\;i = 1,..., n$

(20)

${\left. {{u_x}} \right|_{{\Gamma _j},{\Gamma _j}}} = 0,\;\;j = 1,..., m$

(21)

${\left. {{u_y}} \right|_{{\Gamma _j},{\Gamma _l}}} = 0,\;\;j = 1,..., m$

(22)

${\left. {\bar u} \right|_{{\Gamma _b}}} = \bar 0$

(23)

${\left. {\tilde \sigma \cdot \bar n} \right|_{{\Gamma _b}}} = \rho \bar gz$

(24)

${\left. {\tilde \sigma \cdot \bar n} \right|_{{\Gamma _u}}} = \rho \bar gz$

(25)

$- \bar n \cdot \bar q\left| {_{{\Gamma _l},{\Gamma _u},{\Gamma _b}}} \right. = 0$

(26)

$- \bar n \cdot \rho \bar v\left| {_\Gamma = 0} \right.$

(27)

$\begin{aligned}&{\left. T \right|_{{\Gamma _j}}} = {T_1}\left( {t,x} \right) \\&{T_1}\left( {t,x} \right) = - ({T_{pod}}(t) - {T_{obr}}(t))x/{h_1} + {T_{pod}}(t),\;j = 1,..., m\end{aligned}$

(28)

where ${T_{{o_i}}}$ is initial temperature of the layer, i is layer number, n is number of layers, j is well number, m is number of wells, ${\Gamma _j}$ is well boundary, ${\Gamma _b}$ is lower boundary of the layer, ${\Gamma _u}$ is upper boundary of the layer, ${\Gamma _l}$ is boundary of the considered area of layered rock mass, $\Gamma \!=\! {\Gamma _l} \cup {\Gamma _b} \cup {\Gamma _u} \cup {\Gamma _j}$ , T_pod is temperature of coolant supply, T_obr is coolant return temperature, and h₁ is depth of freeze wells. It is assumed that pore pressure, Darcy's velocity, initial displacement of the solid skeleton are zero, and initial temperature of each layer is known from geophysical investigations. Horizontal displacements and heat flux on the outer boundaries of the considered area are zero. Lithostatic pressure on the boundaries of the layers corresponds to the given depth. Zero horizontal displacements and linear temperature gradient are prescribed on the walls of the freezing wells. The temperature on the bottom of the wells is equal to the temperature of the coolant supply; the temperature on the wellhead is equal to the return temperature of coolant.

3 Initial data 3.1 Location and operation mode of the freezing wells

The initial data were generated close to real observed situation. Artificial freezing zone includes 41 freezing well. Centers of these wells are located on the circle which has a diameter of 10.5 m and are located at a distance of 1,608 mm from each other. The diameter of the freezing well is 146 mm and its depth is 225 m. To simulate influence of the real geometry of the wells after drilling, artificial inclinometer data were generated. Deviation of the bottom of each well from the vertical was taken into account during the simulation. Inclinometer data are presented in Table 1.

Data on the coolant temperature supply and return presented in Table 2 were used to define boundary conditions.

3.2 Structure of the rock mass and its physical properties

According to geological data, sedimentary cover consists of 30 layers up to a depth of 225 meters. All 30 layers were grouped into 13 layers with similar thermophysical properties and permeability. Averaged properties of each layer were calculated as the arithmetic mean of the physical properties combined in one group. The averaged thermophysical properties of the layers are presented in Table 3. The following abbreviations are used in the Table 3: ρ_p is density of soil particles (kg/m³), T_cr is crystallization temperature of water in the layer (K).

Averaged mechanical properties of the layers are presented in Table 4.

4 Numerical simulation of artificial ground freezing in the fluid-saturated rock mass 4.1 Finite-element model of the considered area

The considered area is a cylinder with a depth of 225 meters and diameter of 26.5 meters. This area has been divided by finite elements which have a form of rectangular prisms. The size of the finite element was 9~11 centimeters in the vicinity of the well and 6~7 meters in the periphery. The height of the elements was no more than 6 meters. Finite element model of one of the layers is demonstrated in Figure 1. The total number of elements was about 1 million.

4.2 Initiation and evolution of the ice wall

Numerical solution of the coupled boundary value problem of artificial ground freezing for the time interval of 300 days was obtained. Figure 2 and 3 show evolution of the phase transition front.

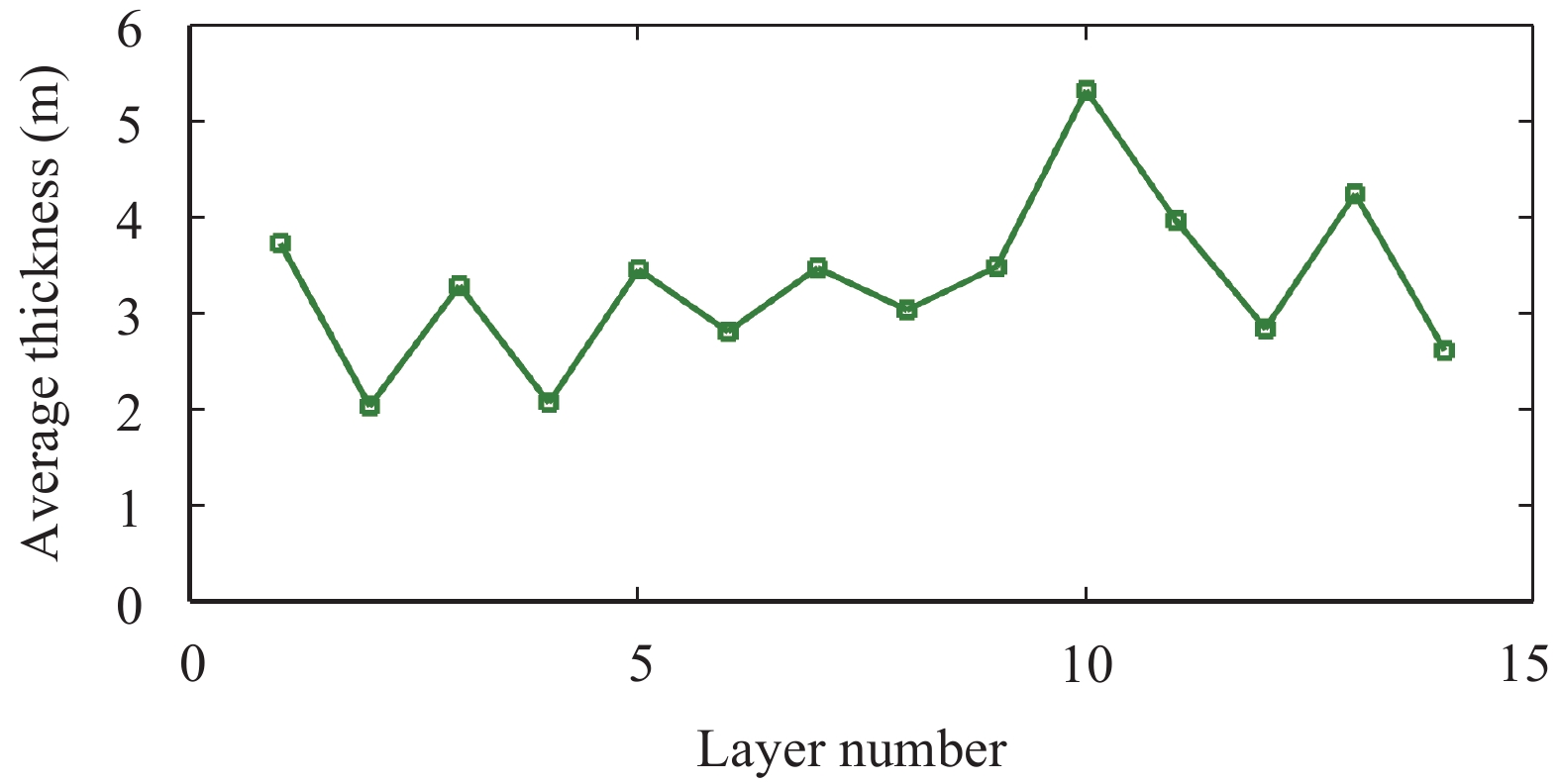
Average thickness of the ice wall after 282 days was calculated in order to estimate thickness variation. The results are presented in Figure 4. Average thickness of the ice wall is 3.32 meters (standard deviation is 0.86 m).

4.3 Seepage flow accompanying ice wall formation

An important factor affecting the process of ice wall formation is seepage flow of the fluid filling pore space. Moving fluid is a convective source of heat transfer. A change in the fluid pressure or density due to the phase transition leads to change in the stress-strain state of the solid skeleton.

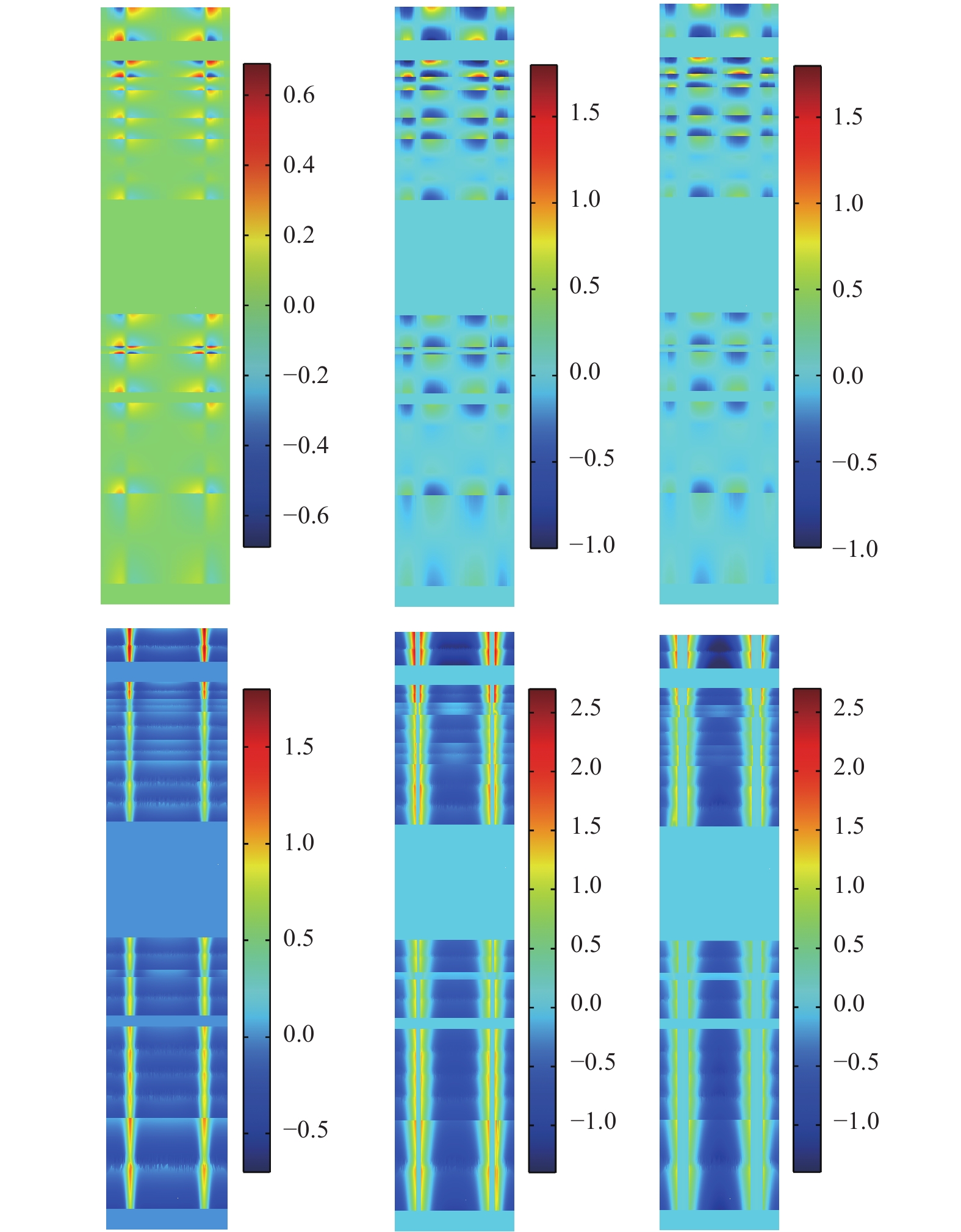
Figure 5 shows distribution of the vertical and horizontal component of the Darcy's velocity in the xOz section in various time moments after the beginning of the freezing process. Z axis is directed downward.

Distribution of the horizontal component of the Darcy's velocity shows characteristic "mosaic" structure of the alternating areas with a multidirectional fluid motion. The velocity amplitude varies from layer to layer within ±1.6 millimeters per day.

In the vertical direction the fluid rises up along the wells and boundaries of the ice wall. After that, it changes direction. Amplitude of the Darcy's velocity exceeds the amplitude of the horizontal component and varies within ±2.5 millimeters per day. The presented figures of the Darcy's velocity field indicate the presence of convective flows of a certain topology near the wells. Structure of these flows can be seen more clearly in Figure 6.

Analysis of the obtained stream lines shows that after the beginning of the phase transition process formation, two toroidal convective cells are observed. One is formed inside of the ice wall and the other is formed outside of the ice wall. Fluid filling pore space rises up along the cold walls of the freezing arch inside of each cell. Furthermore, the fluid moves along the layer boundary and goes down in the middle of the inner surface of the freezing arch in the second cell and along the lateral boundaries in the first cell. Thus, after the beginning of the phase transition process, seepage flows induced by thermo-gravitational convection are observed in each layer with the nonzero permeability.

4.4 Effect of constant seepage flow in the layer on the ice wall formation

The hypothesis of the immobility of groundwater in the aquifers (relative to time if ice wall formation) is quite rough because the presence of the constant seepage flow can be induced by the peculiarities of the geological structure of the region as well as its geodynamic behavior. Series of numerical experiments on the ice wall formation in the most heat-conducting layer (layer 10) with a sufficiently high permeability were carried out in order to investigate the effect of these flows on the phase transition rate. Moreover, the 10^th layer has a pronounced spreading of the freezing wells location in the vertical direction relative to location of the wellheads.

Numerical simulation was carried out in the aforementioned coupled mathematical formulation. Constant horizontal seepage flow in the layer was simulated by applying Darcy's velocity to the left and right boundaries of the layer. The calculations were made for the three values of the seepage flow velocities: 17.3, 65 and 173 millimeters per day. In case of the zero seepage flow the ice wall closure is observed on the 70 th day. Temperature distribution after 50 and 150 days from the beginning of the freezing process is presented in Figure 7. All results are presented for the central section of the computational area by the xOy plane.

In case of the presence of horizontal seepage flow with a velocity of 17.3 millimeters per day (minimum of the considered velocities) ice wall closure is observed 38 days later than in the case of the absence of such flow (108 days after the beginning of the freezing process). Figures 8 and 9 represent evolution of temperature and second phase (ice) distributions.

These distributions show that the fluid flow induces insignificant transfer of cold water from the zone of the ice wall formation. In case of the presence of several non-closed zones, flow inside of the ice wall shifts for the outflow of the fluid through these zones, thereby making the closure even more difficult. Figure 10 presents distribution of the y-component of the Darcy's velocity. It can be noted that fluid velocity in these zones increases significantly. After 50 days from the beginning of the freezing process fluid velocity in the non-closed areas exceeds prescribed flow on the boundaries 8.5 times (fluid velocity is about 140 mm per day).

Abutting into the ice wall fluid flow induces exceeding of the pore pressure which is leveled in the region outside of the ice wall (Figure 11). The value of the pressure jump does not exceed 5% of the hydrostatic pressure at this depth. In case of constant flows with velocities of 65 and 173 mm per day, complete closure of the ice wall are not observed for the considered time (300 days) and influence of the flow on the ice wall formation is the most pronounced (Figure 12).

According to the obtained results, transfer of the cooled fluid by the flow is very significant. Therefore, there are closure and growth of the two disconnected ice zones on both sides of the flow and creation of the two separate ice clusters between them, integration of which is difficult. Fluid velocity between separate clusters increases from 6 (prescribed velocity is 173 mm per day) to 8 (prescribed velocity is 65 mm per day) times as well as in the case of the minimum prescribed velocity (Figure 13). In addition to the increase in the value of the horizontal fluid velocity component there is observed insignificant vertical component which does not exceed 0.2% of the y Darcy's velocity component (Figure 14).

Due to the non-uniform thickness of the ice wall (because of the vertical temperature gradient of the refrigerant) before the phase transition front vertical component of the Darcy's velocity field has a positive direction (Figure 14) which does not depend on the velocity of the seepage flow in the layer. There is observed local increase in pore pressure ahead of the ice wall at velocities of 65 and 173 mm per day as well as in the case of the minimal seepage flow (Figure 15). Pore pressure variations do not exceed units of percent of the hydrostatic pressure corresponding to this depth.

Thereby, results of the simulation show that presence of the horizontal seepage flow significantly affects ice wall formation by slowing its growth.

5 Summary

This study is devoted to the development of a multiphysics model for the artificial ground freezing process. The proposed model includes solution to several problems: the problem of non-stationary thermal conductivity with phase transition, the problem of linear filtration, and the problem of thermo-elasticity. This model is based on the following hypotheses: isotropy of physical properties in the rock layers, the absence of the unfrozen water after phase-transition, small deformation of the porous media, and weak compressibility of the fluid.

The proposed model was used for the numerical simulation of the ice wall formation in water-infiltrated soil designed for the construction of a vertical mine at Starobinsk deposits taking into account accompanying filtration and mechanical processes. Numerical simulation was carried out by the finite-element method. This paper has detailed information on issues concerning determination of material parameters.

Results of numerical simulation allowed us to define time of the ice wall closure, thickness of the ice wall in each layer, and average thickness of the whole ice wall. It has been shown that ice wall forms non-uniformly. This can be connected with deviations of the wells from the vertical as well as with the difference in thermal and filtration properties of the layers. Analysis of the stream lines distribution shows that after the beginning of the phase transition, formation of two toroidal convective cells was observed. One is created inside the ice wall while the other is created outside of the wall. The fluid filling the pore space rises up along the cold walls of the ice wall, moves along the layer boundary and goes down in the middle of the inner region of the ice wall in the second cell and along the lateral boundaries in the first cell. Thereby, there are observed seepage flows induced by the thermo-gravitational convection after the beginning of the phase transition in each layer with the non-zero permeability.

The influence of constant horizontal seepage flow on the ice wall formation was investigated. Numerical simulation of the ice wall formation in the layer with a seepage flow with several prescribed velocities (17.3, 65 and 173 millimeters per day) was carried out. Results of the simulation show that in the case of the absence of the flow, the closure of the ice wall is observed after 70 days from the beginning of the freezing process. In case of the presence of the flow with the minimal considered velocity (17.3 millimeters per day), the closure is observed 38 days later (after 108 days). In case of the fluid flow with the velocities of 65 and 173 millimeters per day, complete closure of the ice wall was not observed for the considered time (300 days). Thereby, results of the simulation show that presence of the horizontal seepage flow significantly affects ice wall formation.

Acknowledgments:

This work was supported by the Russian Science Foundation (Grant No. 17-11-01204).