Surface soil moisture (Ms) is an important factor in many fields of study, such as meteorology, hydrology, and ecology (Pultz et al., 1997 ; Dirmeyer, 2000; Le Hégarat-Mascle et al., 2002 ; Yang et al., 2016 ); it also has important applications in estimating crop yield and drought monitoring (McNairn et al., 2012 ). With the development of the economy in the arid area of Northwest China, where rainfall is scant, the shortage of water resources is becoming more and more severe, making it more important to obtain timely distribution of the soil moisture in a certain range. Remote-sensing technology has shown great ability to estimate soil moisture, as compared to optical and passive microwave remote sensing. Active remote sensing has its own special advantage in soil-moisture estimation, and many empirical and semi-empirical models have been developed to estimate soil moisture (Oh et al., 1992 ; Dubois et al., 1995 ; Shi et al., 1997 ). Current empirical and semi-empirical models are suitable for a certain range of surface roughness. Recently, the integral equation model (IEM) was developed and widely used in simulating backscattering of bare soil or sparsely vegetated landscapes. Based on the model, surface soil-moisture information can be obtained (Fung, 1994; Rahman et al., 2008 ). Based on IEM, Chen et al. (2003) developed the Advance Integral Equation Model (AIEM) to simulate backscattering of bare soil or sparsely vegetated landscapes, with a good result showing that it is useful for soil-moisture estimation over a bare soil surface. Generally, when using AIEM to simulate backscattering of bare soil, two important input parameters—soil moisture and surface roughness—are unknown; and other input parameters such as radar configuration are known. To estimate soil moisture, the impact of surface roughness on backscattering must be removed, using multi-angle and multi-polarized data to establish the relationship between backscattering and surface roughness (Zribi and Dechambre, 2003; Baghdadi et al., 2006 ; Gherboudj et al., 2011 ). The objective of this study is to present a method to estimate soil moisture over bare agricultural fields, using RADARSAT-2 high- and low-incidence-angle mode data, based on the AIEM.
2 Study area and data processing 2.1 Study areaThe study area is located in the city of Dunhuang, west of the Hexi Corridor, in Northwest China (Figure 1a). Dunhuang falls in an arid climatic zone, with an annual average rainfall of about 39.9 mm; but the annual mean evaporation reaches 2,486 mm. Dunhaung oasis is surrounded by the Gobi Desert, water needed for both daily and irrigation depending on glacier-melt water from the Qilian Mountains. The shortage of water resources has become an important problem in this area, making it important to be able to estimate surface soil moisture over agricultural fields in this arid area (Liu et al., 2017 ).

|
Figure 1 Location of the study area of Dunhuang (a) and the satellite remote-sensing experiment plot (b) (Landsat TM imagery, bands 4, 3, 2) |
RADARSAT-2 was launched in December of 2007 by the Canadian Space Agency. It is an earth-observing satellite offering powerful technical advancements that enhance marine surveillance, ice monitoring, disaster management, environmental monitoring, resource management, and mapping, RADARSAT-2 works at C-band (5.405GHZ), providing 11 kinds of beam mode data, with different resolutions and incidence angles. The incidence angles range from 10° to 60°. Two RADARSAT-2 images were acquired over the Dunhuang study area: the high-incidence-angle mode data (May 13, 2015), with a 53.3° average incidence angle, HH polarization; and the low-incident-angle mode data (May 12, 2015), with a 16.5° average incidence angle, HH polarization. The image data are single-look complex (SLC) data; the image digital numbers (DN) are in units of amplitude; and the DN value should be converted to backscattering values (σ) before using. The computation of σ is
| $\sigma = 10 \times \lg \left[\left(\frac{{D{N^2} + {A_0}}}{{{A_1}}}\right)\times \sin (I)\right]$ | (1) |
where σ is the radar backscattering coefficient in decibel units (dB), DN is the image digital numbers, A0 and A1 are the automatic gain control, and I is the incidence angle. The NEST (Next ESA SAR Toolbox) software was used on the image for radiometric calibration.
A median filter consisting of a 9-pixel moving window was applied to reduce RADARAT-2 SAR data speckle (Thoma et al., 2006 ). Based on the 1:50,000 relief maps, ground control points were chosen; and the RADARSAT-2 backscattering image data were georectified.
2.3 Ground observationsField campaign measurements of soil-surface roughness and soil moisture were conducted when the RADARSAT-2 satellite passed over on May 12, 2015. Soil-surface roughness was measured using a 1.5-m profile of a pin meter. For the 26 experimental sites, roughness was computed by averaging the roughness parameters (the root mean square height (s) and the correlation length (l)) obtained from three sparsely distributed measurement points. Soil moisture at the surface was measured for three depths: 0–7.5 cm, 0–12 cm and 0–20 cm using the TDR300 at the time of the RADARSAT2 overpasses. The three different depths of soil moisture were also computed by averaging the soil-moisture readings obtained from three sparsely distributed measurement points.
The correlation between radar backscattering and soil moisture of different depths was analyzed, as shown in Table 1. It is shown that low-incidence-angle SAR data are more sensitive to soil moisture. For high- and low-incidence-angle radar backscattering, there is a better relationship between SAR data and moisture in the top 0–20 cm of soil.
|
|
Table 1 The correlation coefficient between backscattering of two incidence-angle mode data and soil moisture of three different depths |
In this paper, we use AIEM to simulate radar backscattering. The values of the main input parameters—including soil moisture, roughness, incidence angle, and soil temperature—were set based on the ground experiment. The soil temperature was set at 20 °C. The incidence angle was set according to low-incidence-mode RADARSAT-2 data, which was 16.5°. Seven different s values were chosen, ranging from 0.1 cm to 1.3 cm; three different l values were chosen, ranging from 5 cm to 11 cm; and five different Ms values were chosen, ranging from 10% to 60%. Based on the input parameters, the HH polarization backscattering was simulated using AIEM.
In earlier studies, the influence of soil roughness on backscattering considered only the root mean square height (s), neglecting the effect of l. Based on comprehensive consideration of the influence of s and l on the radar backscattering, a roughness parameter was used, where Zs=s2/l (Zribi and Dechambre, 2003). Figure 2 shows the effect of s (Figure 2a) and Zs (Figure 2b) on radar backscattering; the mixed-roughness parameter Zs is more accurate to simulate radar backscattering.
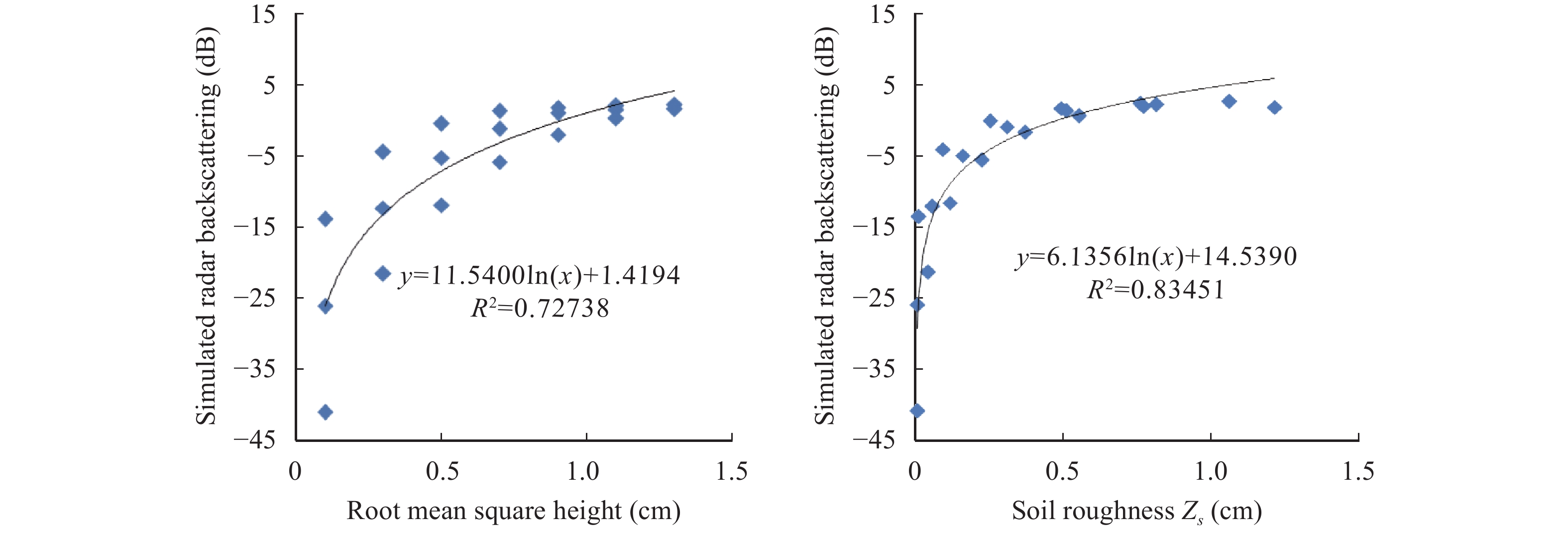
|
Figure 2 Illustration of the effect of root mean square (a) and soil roughness Zs (b) on radar-signal simulations at 16.5° incidence angle |
To analyze the influence of soil moisture and soil roughness on radar backscattering, the l was set to one value (l=8 cm), which can simplify the analysis of the relationship. Considering one value for the l has no influence on our conclusions in this section. Then, the influence of soil moisture and roughness on radar backscattering is simulated, as shown in Figure 3.
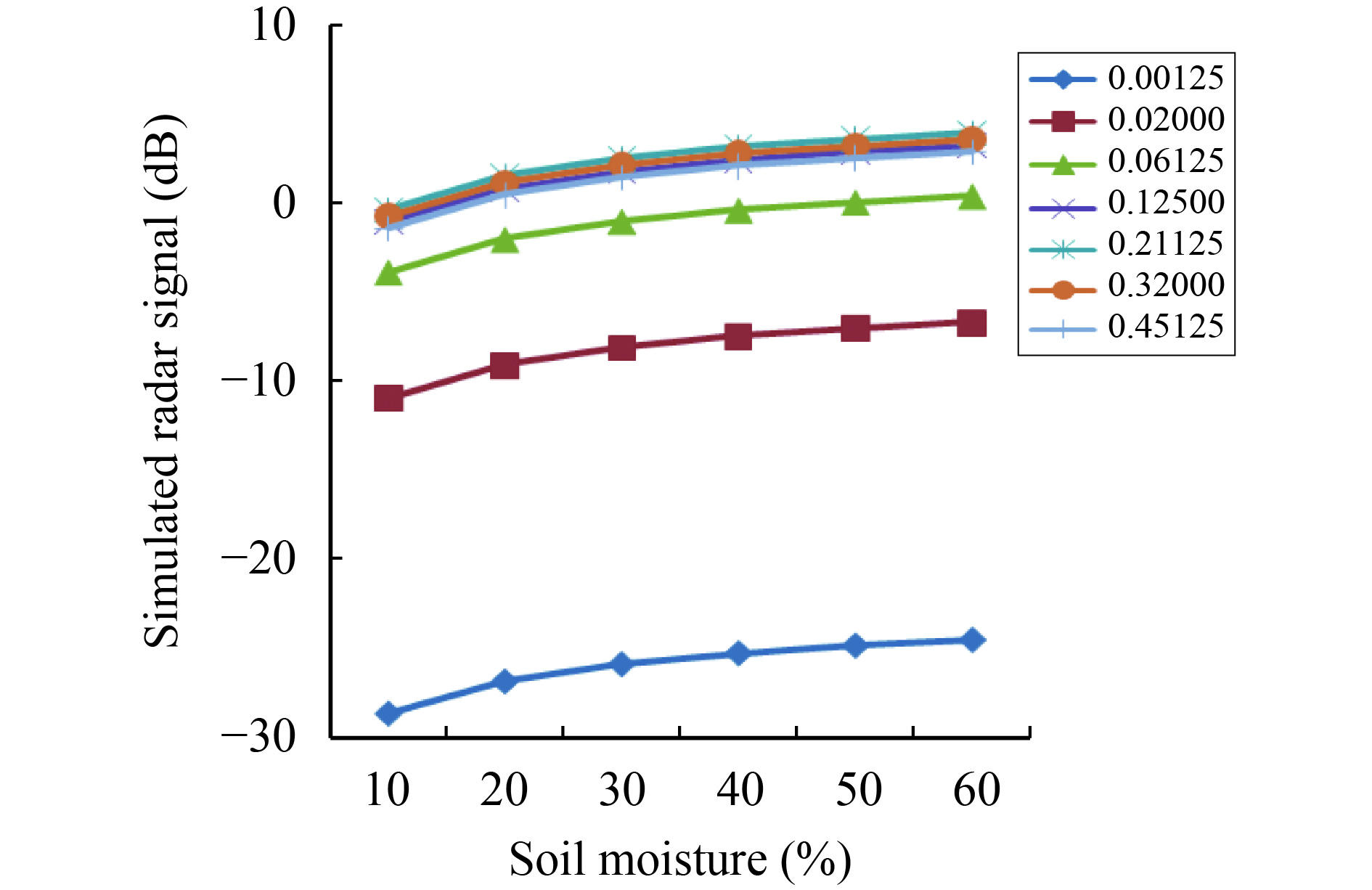
|
Figure 3 Illustration of the influence of soil moisture and roughness on radar-backscattering simulations |
As shown in Figure 3, the influence of soil moisture on backscattering is approximately independent of the soil-roughness parameter; and the influence of roughness on radar backscattering is also approximately independent of the soil moisture. Our conclusions are similar to those of Zribi et al. (2005) . We also find that the relationship is logarithmic between the radar backscattering (σ) and soil moisture (Ms) and soil roughness (Zs) for the RADARSAT-2; and radar backscattering (σ) can expressed as a function of Ms and Zs, where
| $\sigma = a\ln {M_s} + b\ln {Z_s} + c$ | (2) |
In section 2.3, we found that low-incident-angle mode data are more suitable for obtaining soil moisture; so the RADARSAT-2 low-incident-angle radar backscattering can be written by
| ${\sigma _{\rm {low}}} = a\ln {M_s} + b\ln {Z_s} + c$ | (3) |
Based on AIEM, the high-and low-incidence-angle SAR backscattering was simulated. It was also found that the difference in backscattering with two different incidence angles, independent of soil moisture, has a relationship on its own with soil roughness, as shown in Figure 4. Our conclusions are similar to those of Zribi and Dechambre (2003). For the RADARSAT-2 high- and low-incident-angle mode simulated data, the difference (Δσ=σlow−σhigh) between low-incidence-angle radar backscattering (σlow) and high-incidence-angle radar backscattering (σhigh) shows a logarithmic relationship with Zs, where
| ${Z_s} = d \times \ln \Delta \sigma + f$ | (4) |
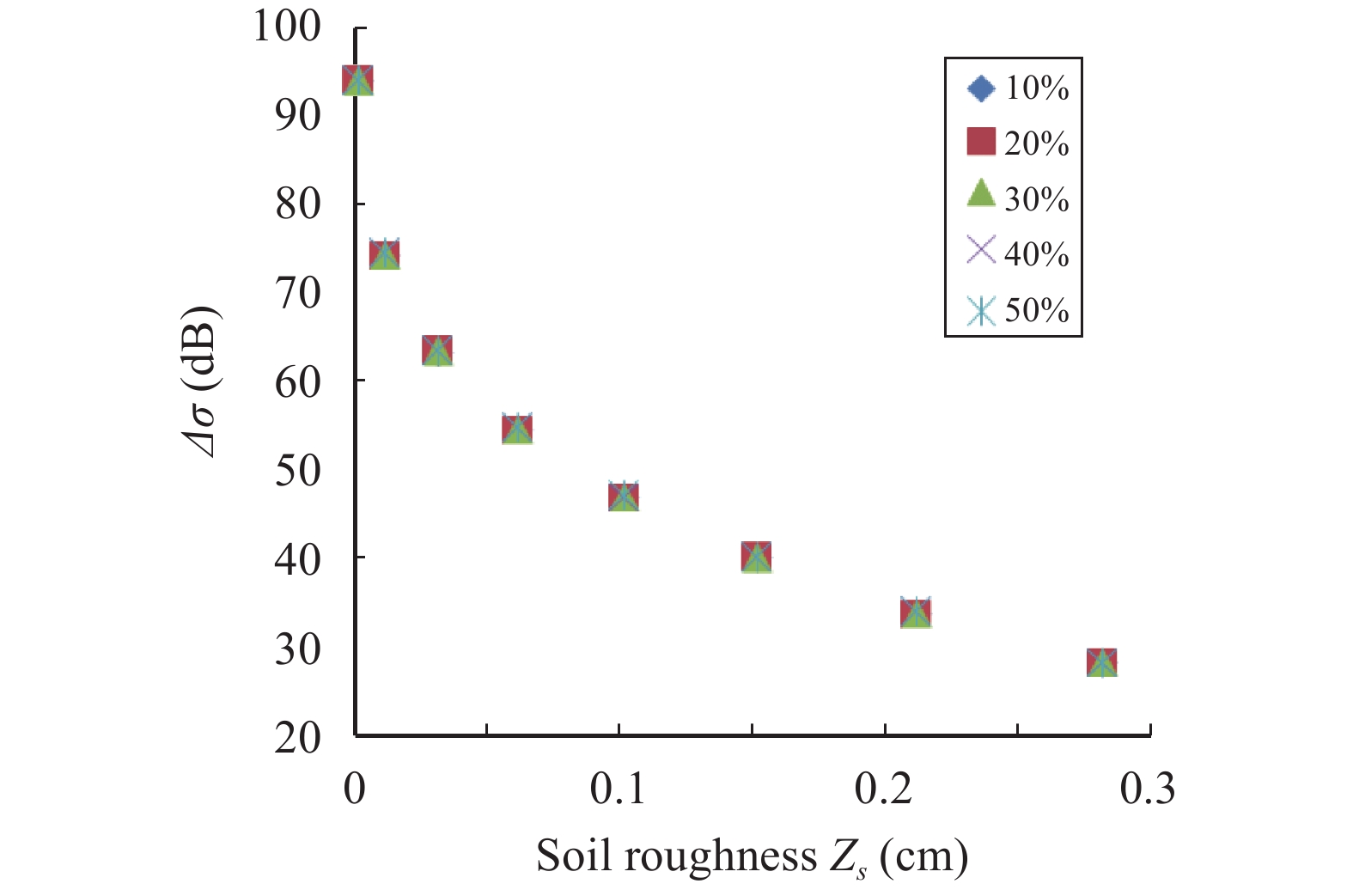
|
Figure 4 Relationship between Δσ (σlow–σhigh) and Zs with five soil-moisture values |
Therefore, the ln(Ms) can be written as Equations (3) and (4):
| $\ln ({M_s}) = \frac{1}{a}{\sigma _{\rm {low}}} - \frac{b}{a}\ln d - \frac{b}{a}\ln (\ln \Delta \sigma + \frac{f}{d}) - \frac{c}{a}$ | (5) |
In Equation (4), we expand
| $\ln {M_s} = {k_1}{\sigma _{\rm {low}}} + {k_2}\ln \Delta \sigma + {k_3}{(\ln \Delta \sigma )^2} + {k_4}$ | (6) |
where k1, k2, and k3 are the coefficients; and k4 is the constant. The ln(Ms) is the function of σlow and Δσ(σlow–σhigh); the coefficients and constant can be calculated by the least-square fitting method, based on the measured data and RADARSAT-2 high- and low-incidence-angle backscattering data.
Based on Equation (6), Ms is obtained using Equation (7).
| ${M_s} = \exp [{k_1}{\sigma _{\rm {low}}} + {k_2}\ln \Delta \sigma + {k_3}{(\ln \Delta \sigma )^2} + {k_4}]$ | (7) |
In section 1.3, the low-incidence-angle SAR backscattering has a better relationship with moisture in the top 20 cm of the soil. Based on the measured data of 26 sites in the Dunhuang study area and the RADARSAT-2 data, k1, k2, k3, and k4 are calculated using SPSS19.0. The ln(Ms) is given by
| $\ln {M_s} = 0.126{\sigma _{\rm {low}}} - 0.139\ln \Delta \sigma + 0.068{(\ln \Delta \sigma )^2} + 5.892$ | (8) |
Then, the soil moisture of the top 20 cm of soil is obtained by Equation (9):
| ${M_s} = \exp [0.126{\sigma _{\rm {low}}} - 0.139\ln \Delta \sigma + 0.068{(\ln \Delta \sigma )^2} + 5.892]$ | (9) |
As shown in Figure 5a, the coefficient of determination between obtained soil moisture and measured soil moisture is 0.85; the RMSE is 4.02%. A linear empirical model describing the relationship between soil moisture and low-incident-angle backscattering data was also built by a regression method based on the 26 plot measurements. The model obtained an RMSE of 7.11% and a correlation coefficient of 0.51. The results show the potential of this method to estimate soil moisture with a high accuracy.
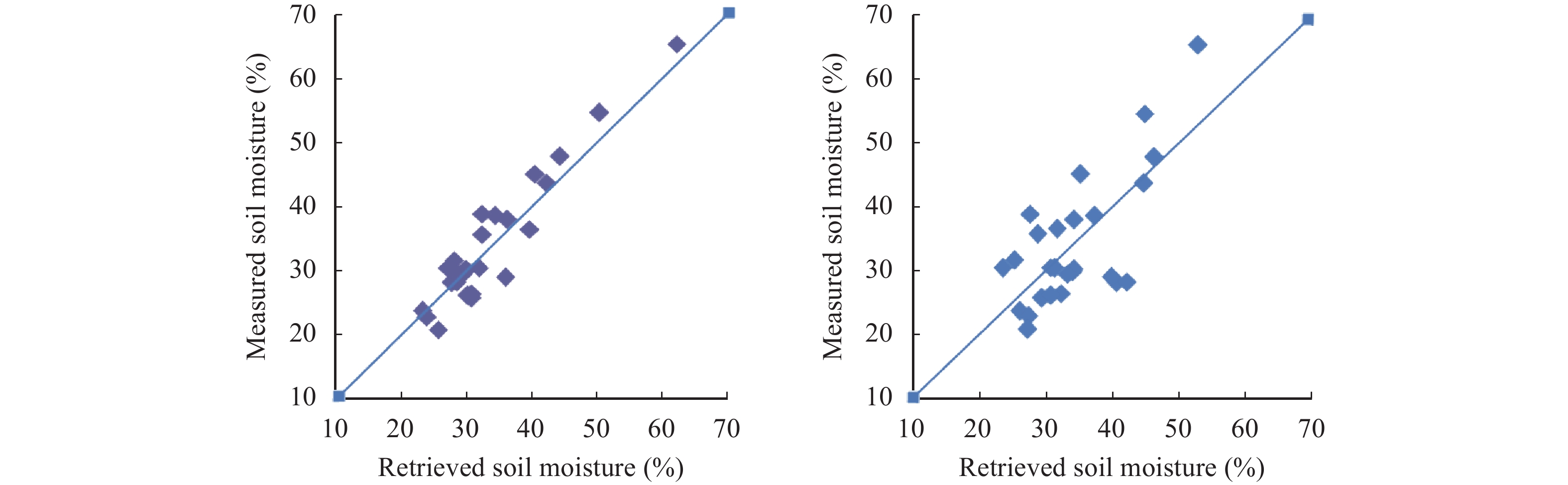
|
Figure 5 Comparison of soil moisture estimates obtained by the model put forward in this paper (a) and the linear empirical model (b) |
A simple soil-moisture estimation method is proposed in this paper. Radar backscattering is mainly influenced by soil moisture and roughness, so soil moisture is a function of radar backscattering and soil roughness. For bare agricultural fields in an arid area, the backscattering of low-incidence-angle RADARSAT-2 data is more sensitive to soil moisture; and a better relationship is found between radar backscattering and the amount of moisture in the top 20 cm of soil. The difference between low- and high-incident-angle radar backscattering shows a logarithmic relationship with soil roughness. Therefore, the estimate of soil moisture is a function of low-incidence-angle backscattering and the difference of low- and high-incident-angle radar backscattering. The natural logarithm of soil moisture is deduced by combining the roughness model and the backscattering model based on the simulated data. By expanding the natural logarithm of soil moisture into a Taylor series, soil moisture can be obtained using the least-square method without having soil-roughness measurements. The results show that the method is useful for estimating soil moisture. Further study is needed with regard to the accuracy of roughness measurements.
Acknowledgments:The study was supported by the National Natural Science Foundation of China (41401408 and 41371027) and the Opening Fund of Key Laboratory of Desert and Desertification, Chinese Academy of Sciences. The authors would like to thank all the experts and editors.
Baghdadi N, Holah N, Zribi M. 2006. Soil moisture estimation using multi-incidence and multi-polarization ASAR data. International Journal of Remote Sensing, 27(10): 1907-1920. DOI:10.1080/01431160500239032 |
Chen KS, Wu TD, Tsang L, et al. 2003. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Transactions on Geoscience and Remote Sensing, 41(1): 90-101. DOI:10.1109/TGRS.2002.807587 |
Dirmeyer PA. 2000. Using a global soil wetness dataset to improve seasonal climate simulation. Journal of Climate, 13(16): 2900-2922. DOI:10.1175/1520-0442(2000)013<2900:UAGSWD>2.0.CO;2 |
Dubois PC, van Zyl J, Engman T. 1995. Measuring soil moisture with imaging radars. IEEE Transactions on Geoscience and Remote Sensing, 33(4): 915-926. DOI:10.1109/36.406677 |
Fung AK, 1994. Microwave scattering and emission models and their applications. Norwood, MA, USA: Artech House, pp. 10–45.
|
Gherboudj I, Magagi R, Berg AA, et al. 2011. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sensing of Environment, 115(1): 33-43. DOI:10.1016/j.rse.2010.07.011 |
Le Hégarat-Mascle S, Zribi M, Alem F, et al. 2002. Soil moisture estimation From ERS/SAR data: toward an operational methodology. IEEE Transactions on Geoscience and Remote Sensing, 40(12): 2647-2658. DOI:10.1109/TGRS.2002.806994 |
Liu YS, Qin X, Du WT. 2017. Changes of glacier area in the Xiying River Basin, East Qilian Mountain, China. Sciences in Cold and Arid Regions, 9(5): 432-437. DOI:10.3724/SP.J.1226.2017.00432 |
McNairn H, Merzouki A, Pacheco A, et al. 2012. Monitoring soil moisture to support risk reduction for the agriculture sector using RADARSAT-2. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5(3): 824-834. DOI:10.1109/JSTARS.2012.2192416 |
Oh Y, Sarabandi K, Ulaby FT. 1992. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Transactions on Geoscience and Remote Sensing, 30(2): 370-381. DOI:10.1109/36.134086 |
Pultz TJ, Crevier Y, Brown RJ, et al. 1997. Monitoring local environmental conditions with SIR-C/X-SAR. Remote Sensing of Environment, 59(2): 248-255. DOI:10.1016/S0034-4257(96)00157-5 |
Rahman MM, Moran MS, Thoma DP, et al. 2008. Mapping surface roughness and soil moisture using multi-angle radar imagery without ancillary data. Remote Sensing of Environment, 112(2): 391-402. DOI:10.1016/j.rse.2006.10.026 |
Shi JC, Wang J, Hsu AY, et al. 1997. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Transactions on Geoscience and Remote Sensing, 35(5): 1254-1266. DOI:10.1109/36.628792 |
Thoma DP, Moran MS, Bryant R, et al. 2006. Comparison of four models to determine surface soil moisture from C-band radar imagery in a sparsely vegetated semiarid landscape. Water Resources Research, 42(1): W01418. DOI:10.1029/2004WR003905 |
Yang JJ, He ZB, Zhao WJ, et al. 2016. Assessing artificial neural networks coupled with wavelet analysis for multi-layer soil moisture dynamics prediction. Sciences in Cold and Arid Regions, 8(2): 116-124. DOI:10.3724/SP.J.1226.2016.00116 |
Zribi M, Dechambre M. 2003. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sensing of Environment, 84(1): 42-52. DOI:10.1016/S0034-4257(02)00069-X |
Zribi M, Baghdadi N, Holah N, et al. 2005. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sensing of Environment, 96(3–4): 485-496. DOI:10.1016/j.rse.2005.04.005 |
 2018, Vol. 10
2018, Vol. 10
