2. University of Chinese Academy of Sciences, Beijing 100049, China
According to the classical wave theory, wave velocity is inextricably interwoven with physical and mechanical parameters of the medium (Li and Li, 1989). The study of wave propagation in different materials has always been an important research subject. It not only has important theoretical and academic value, but also has an important guiding significance for engineering applications. In recent years, with the development of engineering construction in permafrost regions, dynamic characteristics of frozen soils has garnered increased attention for academics and engineers. A porous medium is a material containing pores, with the skeletal portion of the material called the "matrix" or "frame". The pores fill with a fluid (liquid or gas). Many natural substances such as rocks and soil, zeolites, biological tissues, and man-made materials such as cements and ceramics can be considered as porous media. Frozen soil is a porous medium composed of soil particles, pore ice, pore water and gas. Therefore, the propagation theory in porous media is an effective way to study wave propagation characteristics in frozen soil.
Mixture theory and continuum method can used to deal with the problems of multiphase porous media with irregular and complex internal structures (Yang and Yu, 2000). Therefore, Vardoulakis and Beskos (1986) established dynamic equations of unsaturated porous media based on mixture theory, and discussed the wave propagation characteristics of nearly saturated soil in low frequency ranges. Based on the mixture theory, Lu and Hanyga (2004, 2005) established the three-phase dynamic control equations of unsaturated soil, and analyzed the velocity and attenuation characteristics in unsaturated soil by numerical examples. Albers (2006, 2009) established a macro linear model based on the simplified mixture model and focused on analysis of the effects of saturation and excitation frequency on wave velocity and attenuation coefficient in unsaturated porous media. Assuming that the skeleton displacement, water head and temperature are the basic variables, Lu (2001) established two coupling seepage–elastic models, thermal–elastic and thermal–seepage. In addition, the propagation characteristics of saturated soil and unsaturated soil is studied in different angles, and the application of the mixture theory in wave problems is promoted to some extent (Zhou et al., 2008 ; Chen et al., 2012 ; Liu et al., 2014 , 2017; He et al., 2016 ). On the base of existing research of frozen soil, Miao et al. (1995) introduced the mixture theory into the study of the thermodynamic properties of frozen soil to establish a complete constitutive relation.
Based on the Continuum Theory of Mixture, Zhou and Lai (2011) established the elastic wave dispersion equation of porous medium for frozen saturated soil and derived analytical expressions for propagation velocity and attenuation of elastic waves in frozen saturated soil. This theory applied the Bishop effective stress principle and ignored the coupling between components.
Based on the aforementioned results, mixture theory and continuum method play an important role in the study of wave propagation in unsaturated porous media, but most of the coupling between porous media is considered inadequate (Lai et al., 2003 ; Xu et al., 2011 ). With a porous medium consisting of soil skeleton, pore water, pore ice and gas, the equilibrium, deformation compatibility and energy balance conditions of frozen soil is influenced by the coupling of each component. Thus, the coupling between the components cannot be neglected. In this paper, by introducing entropy inequality to describe the coupling between the three-phase saturated soil material and using continuum porous medium method and mixture theory, we derived an analytical expression of wave velocity and attenuation and discussed the wave propagation characteristics in frozen saturated soils.
2 Wave equation for wave propagation in frozen saturated soilIn this paper, frozen saturated soils is considered as a three-phase porous media composed of soil skeleton, pore water and pore ice, designated by the superscripts "s", "w", and "i", respectively. The volume fraction of three-phase composition can be expressed as:
| ${n^s} = 1 - n,\;{n^w} = n\left( {1 - {S_i}} \right),\;{n^i} = n{S_i},$ |
where nα is the volume fraction of three-phase composition; α is used to denote an individual phase, α=s, w, i. Si is the volume ice content, which can be expressed as:
According to the assumption of small deformation and no moment of momentum transfer between the phases, the continuity equation requires that the mass of any matter domain is a constant, so that the continuity equation of frozen saturated soil is:
| $\frac{{\partial \left( {{n^\alpha }{\gamma ^\alpha }} \right)}}{{\partial t}} + {n^\alpha }{\gamma ^\alpha }{\rm {div}}({{{v}}^\alpha }) = 0$ | (1) |
where β is used to denote an individual phase, β=w, i;
For frozen saturated soil, the material time derivative of the momentum of the material system is equal to the effect of physical strength on which collection degree is
| ${\rho ^\alpha }\frac{{D{{{v}}^\alpha }}}{{Dt}} = {n^\alpha }{\rm div}({{{\sigma }}^\alpha }) + {\rho ^\alpha }{{{b}}^\alpha }$ | (2) |
where
Considering the coupling between three phases of frozen saturated soil, entropy is introduced into the second law of thermodynamics in order to express the irreversibility of deformation process. For linear dynamic process of frozen saturated soil, the entropy inequality assumes the following form:
| $- \sum\limits_\alpha {\frac{{{D^\alpha }{\Psi ^\alpha }}}{{Dt}}} + \sum\limits_\alpha {\frac{{{n^\alpha }{{{\sigma }}^\alpha }:{{{d}}^\alpha }}}{{{\rho ^\alpha }}}} - \sum\limits_F {{{{b}}^\beta} \cdot \left( {{{{v}}^\beta } - {{{v}}^S}} \right)} \ge 0$ | (3) |
where
According to previous studies (Wei and Muraleetharan, 2006), Helmholtz free energy of frozen saturated soil can be written as:
| ${\Psi ^s} = {\Psi ^s}\left( {{\gamma ^s},{\varepsilon ^s}} \right);{\Psi ^\beta } = {\Psi ^\beta }\left( {{\gamma ^\beta },{n^\beta }} \right)$ | (4) |
For simplicity, the free energy equations of each component are solved with the following polynomials by the sum decomposition method:
| $\begin{align}& {\Psi ^s}\left( {{\varepsilon ^s},{\gamma ^s}} \right) = {\Psi _\varepsilon }^s\left( {{\varepsilon ^s}} \right) + {\Psi _\rho }^s\left( {{\gamma ^s}} \right)\\& {\Psi ^w}\left( {{n^w},{\gamma ^w}} \right) = {\Psi _n}^w\left( {{n^w}} \right) + {\Psi _\rho }^w\left( {{\gamma ^w}} \right)\\& {\Psi ^i}\left( {{n^i},{\gamma ^i}} \right) = {\Psi _n}^i\left( {{n^i}} \right) + {\Psi _\rho }^i\left( {{\gamma ^i}} \right)\end{align}$ | (5) |
The material derivative of pore water and pore ice are rewritten as:
| $\left\{ \!\! \begin{array}{l}\displaystyle\frac{{{D^w}}}{{Dt}} = \frac{{{D^s}}}{{Dt}} + \left( {{v^w} - {v^s}} \right) \cdot \nabla \\[12pt]\displaystyle\frac{{{D^i}}}{{Dt}} = \frac{{{D^s}}}{{Dt}} + \left( {{v^i} - {v^s}} \right) \cdot \nabla \end{array} \right.$ | (6) |
Substituting Equations (4)–(6) into Equation (3), we obtained the control inequalities of thermodynamics:
| $\begin{align}& \left[ {{n^s}{{{\sigma }}^s} - {\rho ^s}\frac{{\partial {\Psi ^s}}}{{\partial {\varepsilon ^s}}} + {n^s}{{\left( {{\gamma ^s}} \right)}^2}\frac{{\partial {\Psi ^s}}}{{\partial {\gamma ^s}}}{{I}}} \right]/{{{d}}_s}\\[2pt]& \;\;\;\;\; + \left[ {{n^w}{{{\sigma }}^w} + {n^w}{{\left( {{\gamma ^w}} \right)}^2}\frac{{\partial {\Psi ^w}}}{{\partial {\gamma ^w}}}{{I}}} \right]/{{{d}}_w}\\[2pt]& \;\;\;\;\; + \left[ {{n^i}{{{\sigma }}^i} + {n^i}{{\left( {{\gamma ^i}} \right)}^2}\frac{{\partial {\Psi ^i}}}{{\partial {\gamma ^i}}}{{I}}} \right]/{{{d}}_i}\\[2pt]& \;\;\;\;\; + \left[ {n{{\left( {{\gamma ^w}} \right)}^2}\frac{{\partial {\Psi ^w}}}{{\partial {\gamma ^w}}} - {n^2}{S_i}{\gamma ^w}\frac{{\partial {\Psi ^w}}}{{\partial {n^w}}} + {n^2}\left( {1 - {S_i}} \right){\gamma ^i}\frac{{\partial {\Psi ^i}}}{{\partial {n^i}}} - n{{\left( {{\gamma ^i}} \right)}^2}\frac{{\partial {\Psi ^i}}}{{\partial {\gamma ^i}}}} \right]\frac{{{D^s}{S_i}}}{{Dt}}\\[2pt]& \;\;\;\;\; + \left[ { - {{({\gamma ^s})}^2}\frac{{\partial {\Psi ^s}}}{{\partial {\gamma ^s}}} + {{\left( {{\gamma ^w}} \right)}^2}{S_i}\frac{{\partial {\Psi ^w}}}{{\partial {\gamma ^s}}} + \left( {1 - {S_i}} \right){{({\gamma ^i})}^2}\frac{{\partial {\Psi ^i}}}{{\partial {\gamma ^i}}} - {n^w}{\gamma ^w}{S_i}\frac{{\partial {\Psi ^w}}}{{\partial {n^w}}} - {n^i}{\gamma ^i}\left( {1 - {S_i}} \right)\frac{{\partial {\Psi ^i}}}{{\partial {n^i}}}} \right]\frac{{{D^s}n}}{{Dt}}\\[2pt]& \;\;\;\;\; - \left( {{n^w}{\gamma ^w}\frac{{\partial {\Psi ^w}}}{{\partial {n^w}}}\nabla {n^w} - {{\left( {{\gamma ^w}} \right)}^2}\frac{{\partial {\Psi ^w}}}{{\partial {\gamma ^w}}}\nabla {n^w} + {\rho ^w}{{{b}}^w}} \right) \cdot \left( {{v^w} - {v^s}} \right)\\[2pt]& \;\;\;\;\; - \left( {{n^i}{\gamma ^i}\frac{{\partial {\Psi ^i}}}{{\partial {n^i}}}\nabla {n^i} - {{\left( {{\gamma ^i}} \right)}^2}\frac{{\partial {\Psi ^i}}}{{\partial {\gamma ^i}}}\nabla {n^i} + {\rho ^i}{{{b}}^i}} \right) \cdot \left( {{v^i} - {v^s}} \right)\\[2pt]& \;\;\;\;\; \ge 0\end{align}$ | (7) |
To make Equation (7) absolutely valid, the following hypothesis needs to be satisfied:
| $\begin{align}& {{{\sigma }}^s} = {{{\sigma }}^{\bar s}} - {p^s}{{I}}\\& {{{\sigma }}^\beta } = - {p^\beta }{{I}}\end{align}$ | (8) |
where
| $\begin{align}& {p^\alpha } = {\left( {{\gamma ^\alpha }} \right)^2}\frac{{\partial {\Psi ^\alpha }}}{{\partial {\gamma ^\alpha }}}\\& {{{\sigma }}^{\bar s}} = {\gamma ^s}\frac{{\partial {\Psi ^s}}}{{\partial {\varepsilon ^s}}}\end{align}$ | (9) |
Neglecting the free energy produced by strain deviator, the increment of specific free energy of each phase medium can be described as:
| $\begin{align}& \Delta \Psi _\varepsilon ^s\left( {{\varepsilon ^s}} \right) = \frac{1}{{2\gamma _0^s}}{\varepsilon ^s}:C:{\varepsilon ^s},\;\;\Delta \Psi _\rho ^s\left( {{\gamma ^s}} \right) = \frac{1}{{2\gamma _0^s}}{K_s}{(e^{{{s'}}})^2}\\& \Delta \Psi _n^\beta \left( {{n^\beta }} \right) = \frac{1}{{2\gamma _0^\beta }}{\theta _\beta }{(\phi ^{{\beta}})^2},\;\;\;\;\;\Delta \Psi _\rho ^\beta \left( {{\rho ^\beta }} \right) = \frac{1}{{2\gamma _0^\beta }}{K_\beta }{(e^{{{\beta '}}})^2}\end{align}$ | (10) |
where
The state of frozen saturated soil before and after the treatment of external force (static equilibrium state and disturbance after external force) can be described as:
Assuming that the frozen soil deformation is in the small strain range, Equation (1) can be formulated as a linear mass conservation equation:
| ${e^\alpha } = {e^{\alpha '}} + {\phi ^\alpha }$ | (11) |
Using Equation (8)–(10), the following stress-strain relations is obtained:
| $\begin{align}& \Delta {{{\sigma }}^s} = \left[ {{\lambda _s}\left( {{{{\varepsilon }}^s}:{{I}}} \right) + {K_s}{e^{s'}}} \right]{{I}} + 2{\mu _s}{{{\varepsilon }}^s}\\& \Delta {{{\sigma }}^\beta } = {K_\beta }{e^{\beta '}}{{I}}\end{align}$ | (12) |
The Bishop's effective stress formula for frozen saturated soil is expressed as:
| ${{{\sigma }}^{\bar s}} = {{{\sigma }}^s} + \left[ {{S_i}{p^w} + \left( {1 - {S_i}} \right){p^i}} \right]{{I}}$ | (13) |
In addition, to make Equation (7) absolutely established, capillary pressure can be expressed as:
| $\begin{align}{p^c} & = {p^w} - {p^i}\\ & = {\xi _s}{D^s}{S_i} + {\rho ^w}\frac{{\partial {\Psi ^w}}}{{\partial {n^w}}} - n{\rho ^i}\frac{{\partial {\Psi ^i}}}{{\partial {n^i}}}\end{align}$ | (14) |
where
If the volume ice content of frozen saturated soil is given, the relation between capillary pressure and pore water can be described as (Van Genuchten, 1980):
| ${p_c} = \alpha _{vg}^{ - 1}{\left( {{S_i}^{ - 1/{m_{vg}}} - 1} \right)^{{n_{vg}}^{ - 1}}}$ | (15) |
where
We assume that the incremental form of capillary pressure can be described as:
| $\Delta {p_c} = - {\left( {{\alpha _{vg}}{n_{vg}}{m_{vg}}} \right)^{ - 1}}\left[ {{S_{i0}}^{ - 1/n_{vg}} - 1} \right]\left( {n_{vg}^{ - 1} - 1} \right){S_{i0}}^{\left( { - 1/{m_{vg}} - 1} \right)}\Delta {S_i}$ | (16) |
By combining Equation (2), with (10)–(16), we can obtain wave equation of wave propagation in frozen saturated soil:
| $\begin{align}& \rho _0^s\frac{{{\partial ^2}{{{u}}^s}}}{{\partial {t^2}}} - {\xi _w}\left( {\frac{{\partial {{{u}}^w}}}{{\partial t}} - \frac{{\partial {{{u}}^s}}}{{\partial t}}} \right) - {\xi _i}\left( {\frac{{\partial {{{u}}^i}}}{{\partial t}} - \frac{{\partial {{{u}}^s}}}{{\partial t}}} \right) = \left( {{X_{ss}} + n_0^s{\lambda _s} + n_0^s{\mu _s}} \right)\nabla \left( {\nabla \cdot {{{u}}^s}} \right) + n_0^s{\mu _s}{\nabla ^2}n_0^s{\mu _s} + {X_{sw}}\nabla \left( {\nabla \cdot {{{u}}^w}} \right) + {X_{si}}\nabla \left( {\nabla \cdot {{{u}}^i}} \right)\\& \rho _0^w\frac{{{\partial ^2}{{{u}}^w}}}{{\partial {t^2}}} + {\xi _w}\left( {\frac{{\partial {{{u}}^w}}}{{\partial t}} - \frac{{\partial {{{u}}^s}}}{{\partial t}}} \right) = {X_{sw}}\nabla \left( {\nabla \cdot {{{u}}^s}} \right) + {X_{ww}}\nabla \left( {\nabla \cdot {{{u}}^{ww}}} \right) + {X_{wi}}\nabla \left( {\nabla \cdot {{{u}}^i}} \right)\\& \rho _0^i\frac{{{\partial ^2}{{{u}}^i}}}{{\partial {t^2}}} + {\xi _i}\left( {\frac{{\partial {{{u}}^i}}}{{\partial t}} - \frac{{\partial {{{u}}^s}}}{{\partial t}}} \right) = {X_{si}}\nabla \left( {\nabla \cdot {{{u}}^s}} \right) + {X_{wi}}\nabla \left( {\nabla \cdot {{{u}}^w}} \right) + {X_{ii}}\nabla \left( {\nabla \cdot {{{u}}^i}} \right)\end{align}$ | (17) |
where
| $\begin{split}& {X_{ss}} = \frac{{{{\left( {n_0^s} \right)}^2}{K_s}\left( {{\theta _w} + {K_w}} \right)\left( {{\theta _i} + {K_i}} \right)}}{M}\\& {X_{ww}} = \frac{{n_0^sn_0^w{K_w}{\theta _w}\left( {{\theta _i} + {K_i}} \right) + {{\left( {n_0^w} \right)}^2}{K_s}{K_w}\left( {{\theta _i} + {K_i}} \right) + n_0^wn_0^i{K_s}{K_w}{\theta _w}}}{M}\\& {X_{ii}} = \frac{{n_0^sn_0^i{K_i}{\theta _i}\left( {{\theta _w} + {K_w}} \right) + {{\left( {n_0^i} \right)}^2}{K_s}{K_i}\left( {{\theta _w} + {K_w}} \right) + n_0^wn_0^i{K_s}{K_i}{\theta _i}}}{M}\\& {X_{sw}} = \frac{{n_0^sn_0^w{K_s}{K_w}\left( {{\theta _i} + {K_i}} \right)}}{M},{X_{si}} = \frac{{n_0^sn_0^i{K_s}{K_i}\left( {{\theta _w} + {K_w}} \right)}}{M},{X_{wi}} = \frac{{n_0^in_0^w{K_s}{K_w}{K_i}}}{M}\\& M = n_0^s\left( {{\theta _w} + {K_w}} \right)\left( {{\theta _i} + {K_i}} \right) + n_0^w{K_s}\left( {{\theta _i} + {K_i}} \right) + n_0^i{K_s}\left( {{\theta _w} + {K_w}} \right)\end{split}$ |
In order to solve the above wave equation, vector displacement is decomposed, and the vector displacement of each phase medium is decomposed by Helmholtz decomposition theorem. The vector displacement of frozen saturated soil can be expressed as:
| $\begin{align}& \left( {\begin{array}{*{20}{c}}{{n^s}{\rho ^s}} & 0 & 0\\[8pt]0 & {{n^w}{\rho ^w}} & 0\\[8pt]0 & 0 & {{n^i}{\rho ^i}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{{\ddot \varphi }^s}}\\[8pt]{{{\ddot \varphi }^w}}\\[8pt]{{{\ddot \varphi }^i}}\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{{\xi _w} + {\xi _i}} & { - {\xi _w}} & { - {\xi _i}}\\[8pt]{ - {\xi _w}} & {{\xi _w}} & 0\\[8pt]{ - {\xi _i}} & 0 & {{\xi _i}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{{\dot \varphi }^s}}\\[8pt]{{{\dot \varphi }^w}}\\[8pt]{{{\dot \varphi }^i}}\end{array}} \right) = {\nabla ^2}\left( {\begin{array}{*{20}{c}}{{X_{ss}} + n_{}^s{\lambda _s} + 2n_{}^s{\mu _s}} & {{X_{sw}}} & {{X_{si}}}\\[8pt]{{X_{sw}}} & {{X_{ww}}} & {{X_{wi}}}\\[8pt]{{X_{si}}} & {{X_{wi}}} & {{X_{ii}}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{\varphi ^s}}\\[8pt]{{\varphi ^w}}\\[8pt]{{\varphi ^i}}\end{array}} \right)\\& \left( {\begin{array}{*{20}{c}}{{n^s}{\rho ^s}} & 0 & 0\\[8pt]0 & {{n^w}{\rho ^w}} & 0\\[8pt]0 & 0 & {{n^i}{\rho ^i}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{{\ddot \Omega }^s}}\\[8pt]{{{\ddot \Omega }^w}}\\[8pt]{{{\ddot \Omega }^i}}\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{{\xi _w} + {\xi _i}} & { - {\xi _w}} & { - {\xi _i}}\\[8pt]{ - {\xi _w}} & {{\xi _w}} & 0\\[8pt]{ - {\xi _i}} & 0 & {{\xi _i}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{{\dot \Omega }^s}}\\[8pt]{{{\dot \Omega }^w}}\\[8pt]{{{\dot \Omega }^i}}\end{array}} \right) = {\nabla ^2}\left( {\begin{array}{*{20}{c}}{{n^s}{\lambda _s}} & 0 & 0\\[8pt]0 & 0 & 0\\[8pt]0 & 0 & 0\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{\Omega ^s}}\\[8pt]{{\Omega ^w}}\\[8pt]{{\Omega ^i}}\end{array}} \right)\end{align}$ | (18) |
The following general form for the dilatations can be assumed:
| ${\varphi ^\alpha } = {A_\alpha }\exp \left[ {i\left( {\omega t - {k_p}{\theta _1}} \right)} \right],\;{\Omega ^\alpha } = {B_\alpha }\exp \left[ {i\left( {\omega - {k_s}{\theta _2}} \right)} \right]\!\!$ | (19) |
where kp and ks are complex number of P and S waves; ω is the excitation frequency.
Substituting Equation (19) into Equation (18) gives:
| $\begin{align}&\left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\[3pt]{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\[3pt]{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{\varphi ^s}}\\[3pt]{{\varphi ^w}}\\[3pt]{{\varphi ^i}}\end{array}} \right) = 0 \\[3pt]&\left( {\begin{array}{*{20}{c}}{{b_{11}}}&{{b_{12}}}&{{b_{13}}}\\[3pt]{{b_{21}}}&{{b_{22}}}&{{b_{23}}}\\[3pt]{{b_{31}}}&{{b_{32}}}&{{b_{33}}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{\Omega ^s}}\\[3pt]{{\Omega ^w}}\\[3pt]{{\Omega ^i}}\end{array}} \right) = 0\end{align}$ | (20) |
Assuming that Equation (20) has nonzero solutions, the characteristic equations of compressional wave and shear wave can be obtained:
| $\det \left[ A \right] = 0\;\;\;\;\;\det \left[ B \right] = 0$ | (21) |
Rearranging Equation (21) gives:
| $\begin{align}& {J_1}k_p^6 + {J_2}k_p^4 + {J_3}k_p^2 + {J_4} = 0\\& {J_5}k_s^2 + {J_6} = 0\end{align}$ | (22) |
As is shown in Equation (22), three types of compressional (P1, P2 and P3) waves and one kind of shear wave (S) are found in frozen saturated soil. If the excitation frequency ω is given, velocity and attenuation coefficient can be obtained:
| $\begin{align}& {c_{pi}} = \frac{\omega }{{\left| {{\mathop{\rm Re}\nolimits} ({k_{pi}})} \right|}},\;\;\;\;\;\;\;\;{c_s} = \frac{\omega }{{\left| {{\mathop{\rm Re}\nolimits} ({k_s})} \right|}} \\& {\delta _{pi}} = \left| {{\mathop{\rm Im}\nolimits} \left( {{k_{pi}}} \right)} \right|,\;\;\;\;\;\;\;\;{\delta _s} = \left| {{\mathop{\rm Im}\nolimits} \left( {{k_s}} \right)} \right|\end{align}$ | (23) |
where Re and Im denote real and imaginary parts of the complex number, respectively.
4 Numerical results and analysisSections 2 and 3 indicate that the propagation velocity in frozen saturated soil is related to excitation frequency and volume ice content separately. In order to evaluate the influence of excitation frequency and volume ice content on propagation characteristics of frozen saturated soil, the physical parameters are listed in Table 1. Meanwhile, the following parameters are assumed: porosity ns=0.2, excitation frequency range 0–1016 Hz, volume ice content range 0.001–0.999, respectively.
|
|
Table 1 Physical parameters |
Figure 1 shows the variation curves of P1, P2, P3 and S wave propagation velocity with excitation frequency in frozen saturated soil. One can see that with increasing excitation frequency, all wave velocities of four wave types increases. In addition, wave velocities increase sharply in the excitation frequency range of 103–109 Hz, but the wave velocity is almost unchanged outside this excitation frequency range. As presented in Figure 1, the velocity of P1 is largest, followed by S and P2, and the velocity of P3 is the minimum. Among them, the velocity is three orders of magnitude smaller than P3. Take the condition of the excitation frequency of 1010 Hz for example,
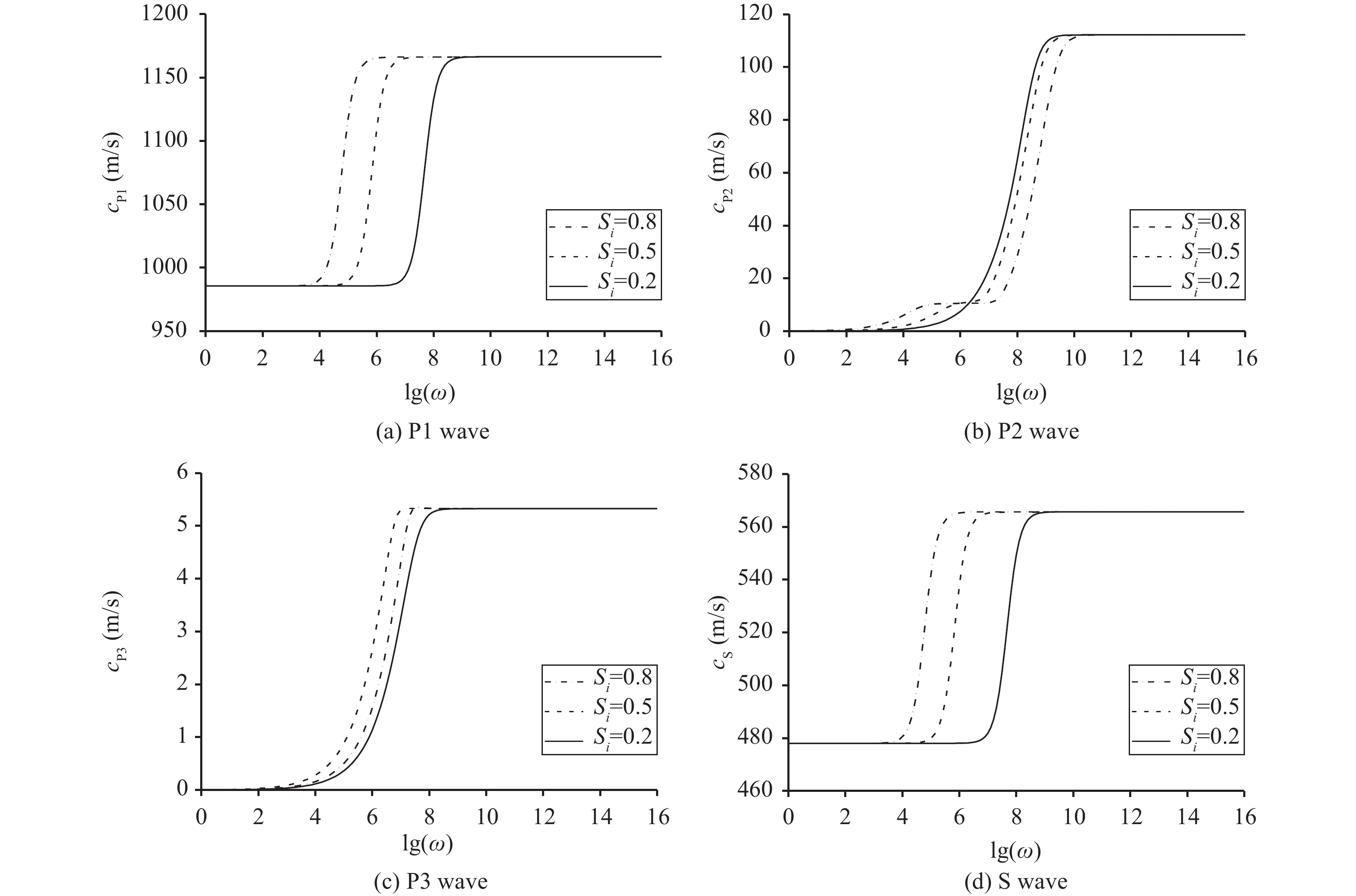
|
Figure 1 Change law of P1, P2, P3 and S wave propagation velocity under different excitation frequency |
Figure 2 shows the variation curves of P1, P2, P3 and S wave attenuation with excitation frequency in frozen saturated soil. One can see that with increasing excitation frequency, all wave attenuations of the four wave types increases, in which the attenuation of P2 and P3 is larger than that of P1 and S. The attenuation law of P1 and S waves is similar to that of magnitude, and it decays rapidly in intermediate-frequency. Take the condition of the excitation frequency is 1010 Hz for example,
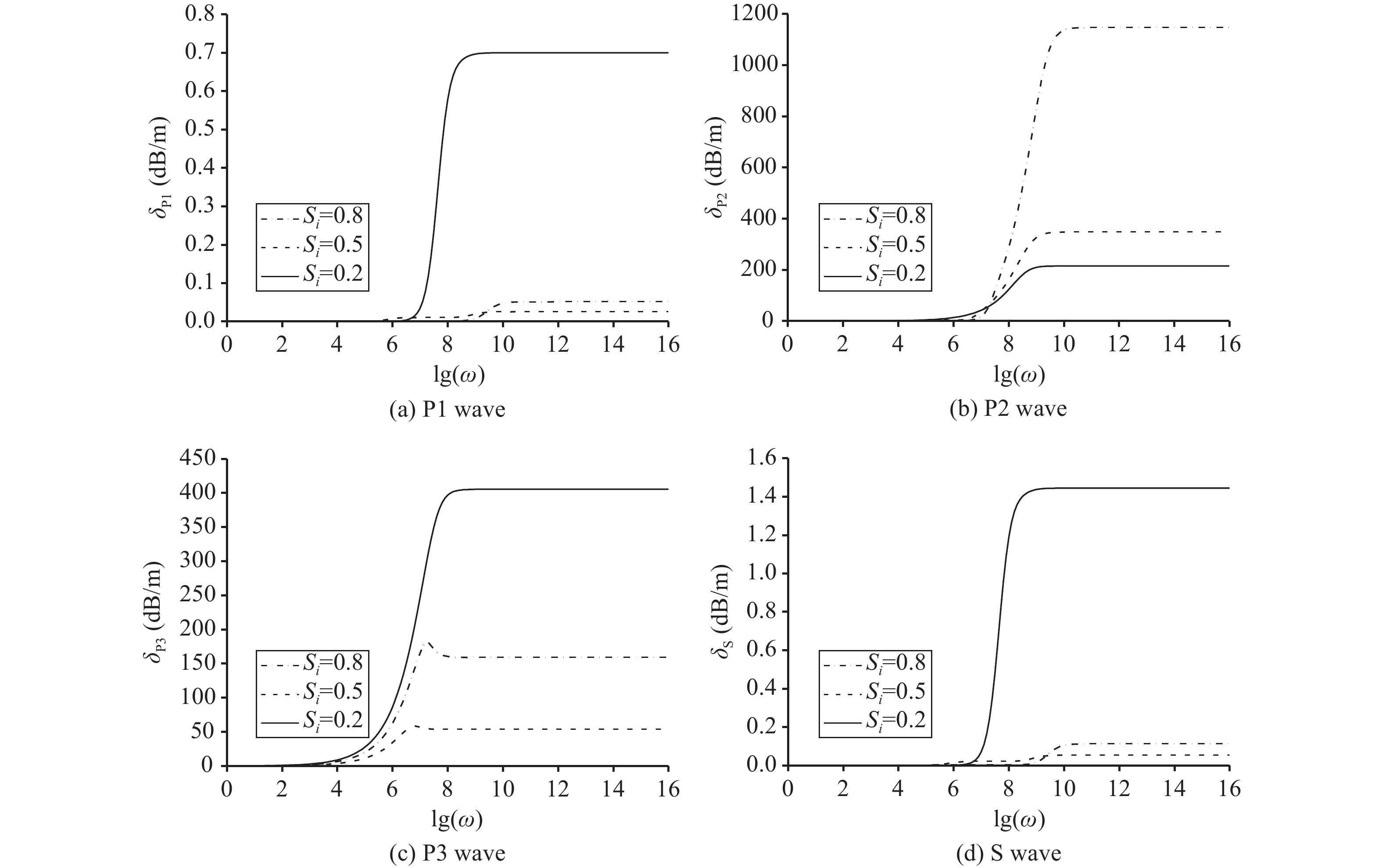
|
Figure 2 Change law of P1, P2, P3 and S wave attenuation under different excitation frequency |
Figure 3 shows the variation curves of P1, P2, P3 and S wave propagation velocity with volume ice content in frozen saturated soil. As can be seen from the figure, there is a resemblance between the propagation law of P1 and S that the wave velocity remained almost unchanged in the low-frequency with an increase of volume ice content. When the volume ice content reached 0.6, the wave propagation velocity decreases dramatically, and the quantity series is close. For example, when the excitation frequency is 105 Hz and volume ice content is 0.9,
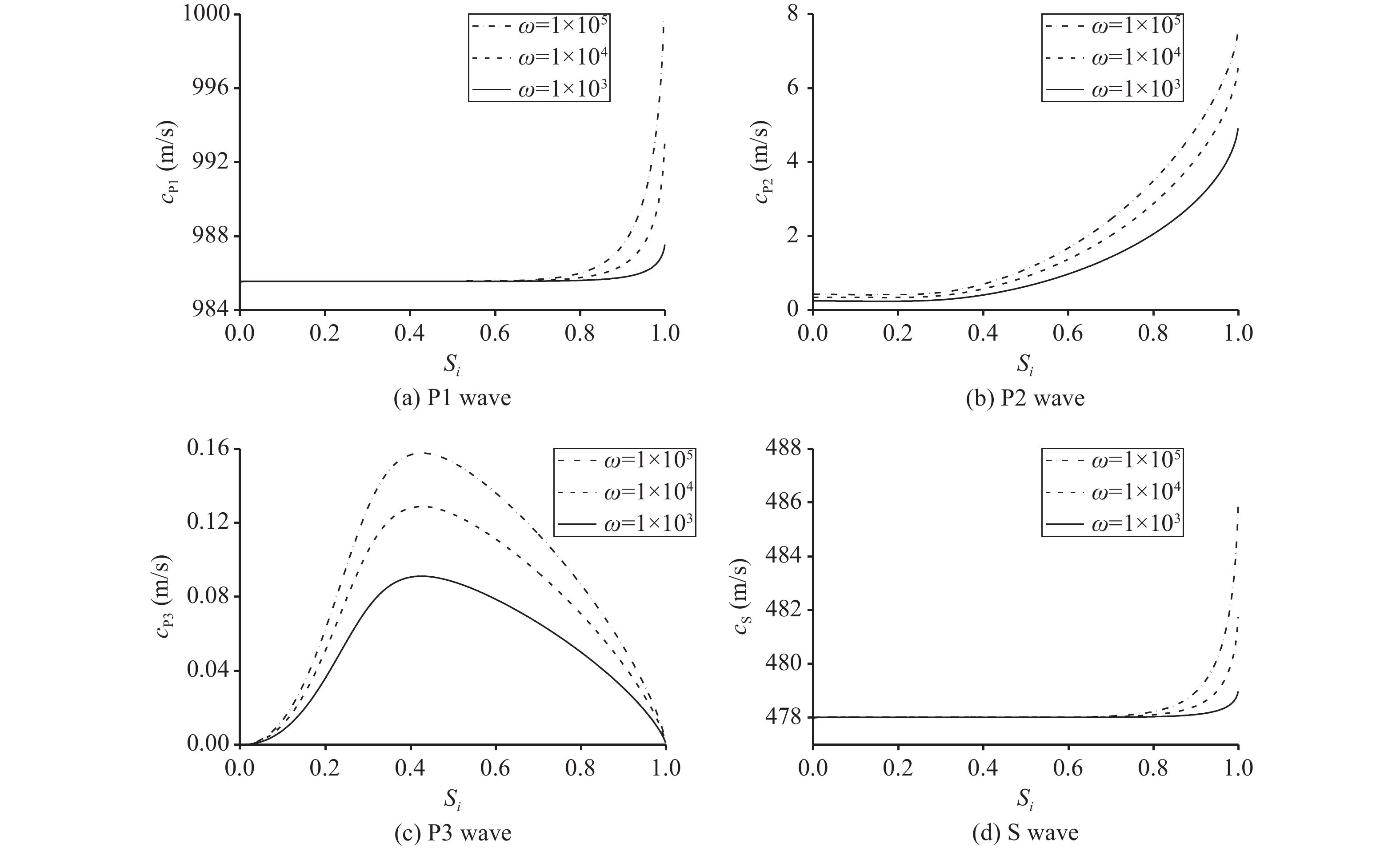
|
Figure 3 Change law of P1, P2, P3 and S wave propagation velocity under different volume ice content |
Figure 4 shows the variation curves of P1, P2, P3 and S wave attenuation with volume ice content in frozen saturated soil. As can be seen from Figure 4, the attenuation coefficient of P1 and S waves begins to increase gradually when the volume ice content is about 0.4. The attenuation coefficient of P2 wave increases first and then decreases with an increase of volume ice content, and there is an obvious inflection point at
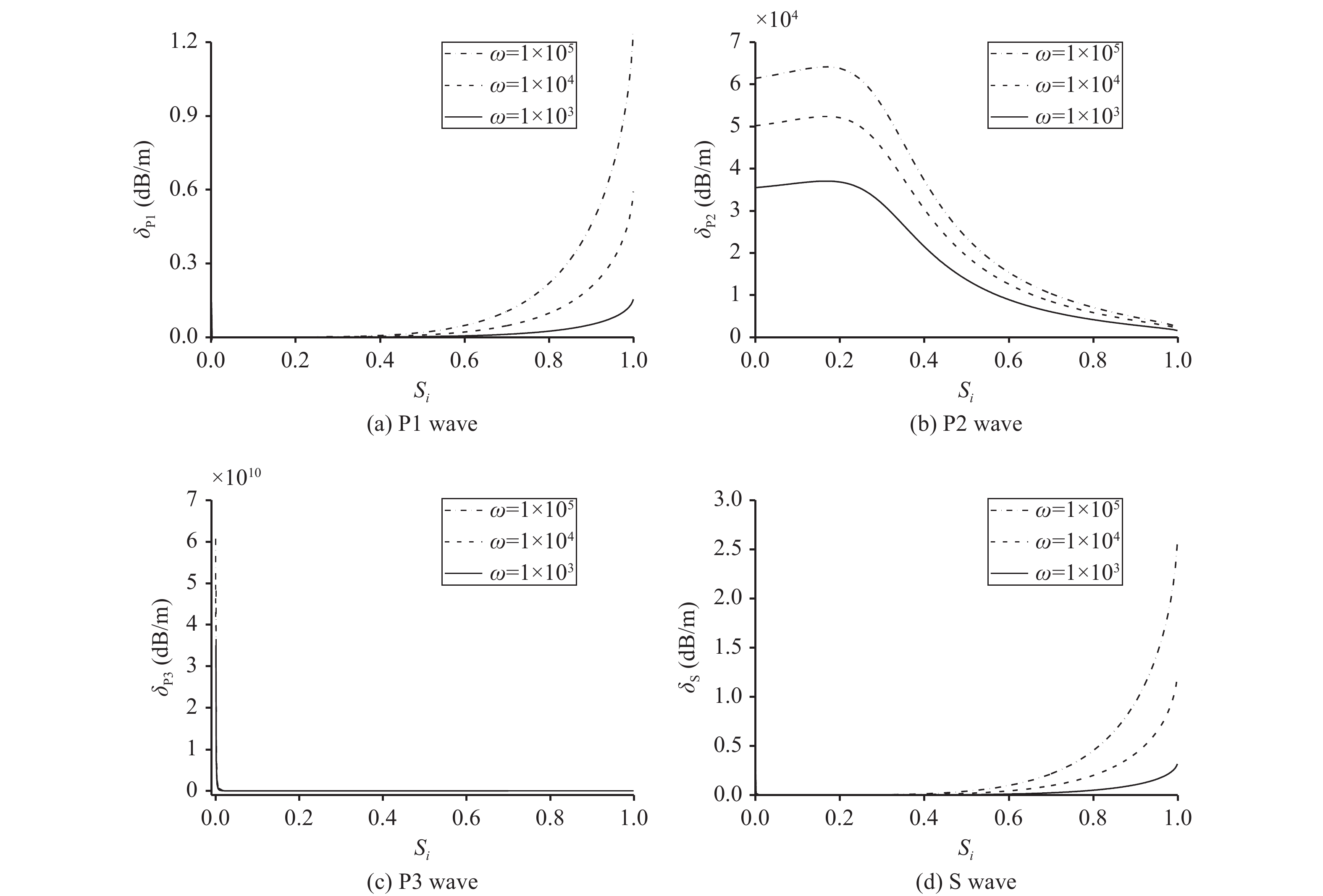
|
Figure 4 Change law of P1, P2, P3 and S wave attenuation under different volume ice content |
This paper is based on continuum porous medium method and mixture theory and considers soil skeleton, pore water and pore ice as fundamental quantities. By introducing entropy inequality to describe the coupling between the three-phase saturated soil material, we derived the analytical expressions of wave velocity and attenuation and discussed the propagation characteristics of waves in frozen saturated soils.
(1) There are three types of compressional waves (P1, P2, P3) and shear wave (S) in frozen saturated soil. The velocity of P1 and S is larger, attenuation is smaller, followed by P2, and P3 wave decays rapidly to zero.
(2) Under increasing excitation frequency, all velocities of four wave types increases and increases sharply in the excitation frequency range of 103–109 Hz, but the wave velocity is almost unchanged outside this excitation frequency range. The attenuation of P2 and P3 waves is larger than that of P1 and S waves. The attenuation law of P1 and S waves is similar to that of magnitude, and the attenuation rate is greatly influenced by volume ice content.
(3) Under increasing volume ice content, the wave propagation velocity of P1 and S waves decreases dramatically when the volume ice content reached 0.6, and the velocity of P2 is increasing gradually. But the P3 wave velocity increases first and then decreases to zero with increasing saturation. The attenuation coefficient of P1 and S waves begins to increase gradually when the volume ice content is about 0.4. The attenuation coefficient of P2 wave increases first and then decreases with the increase of volume ice content. The attenuation coefficient of P3 wave increases with the volume ice content and decreases rapidly from extreme to zero.
(4) Due to the existence of ice particles in frozen soil, the wave propagation characteristics of frozen soil are different from those of unfrozen saturated soil. The wave propagation velocity in frozen saturated soil increases with volume ice content because waves travel faster in ice than in water. Under the one volume ice content, the phenomenon of the existence of an inflection point in the velocity curve of S wave is related to the characteristics of shear wave. As a result, in frozen saturated soils, volume ice content has an intimate relationship with the wave propagation characteristics.
Acknowledgments:This work is supported by the National Natural Science Foundation of China (No. 41271080 and No. 41701060) and the funding of the State Key Laboratory of Frozen Soil Engineering (No. SKLFSE-ZT-17).
Albers B. 2006. On results of the surface wave analyses in poroelastic media by means of the Simple Mixture Model and the Biot model. Soil Dynamics and Earthquake Engineering, 26(6–7): 537-547. DOI:10.1016/j.soildyn.2006.01.007 |
Albers B. 2009. Analysis of the propagation of sound waves in partially saturated soils by means of a macroscopic linear poroelastic model. Transport in Porous Media, 80(1): 173-192. DOI:10.1007/s11242-009-9360-y |
Chen WY, Xia TD, Chen W, et al. 2012. Propagation of plane P-waves at the interface between an elastic solid and an unsaturated poroelastic medium. Applied Mathematics and Mechanics, 33(7): 781-795. DOI:10.3879/j.issn.1000-0887.2012.07.001 |
Hanyga A. 2004. Two-fluid porous flow in a single temperature approximation. International Journal of Engineering Science, 42(13–14): 1521-1545. DOI:10.1016/j.ijengsci.2004.04.001 |
He PF, Xia TD, Liu ZJ, et al. 2016. Reflection of P1 wave from free surfaces of double-porosity media. Rock and Soil Mechanics, 37(6): 1753-1761. DOI:10.16285/j.rsm.2016.06.028 |
Lai YM, Zhang LX, Xu WZ, et al. 2003. Temperature features of broken rock mass embankment in the Qinghai-Tibetan railway. Journal of Glaciology and Geocryology, 25(3): 291-296. DOI:10.3969/j.issn.1000-0240.2003.03.009 |
Li DQ, Wu ZW, Fang JH, et al. 1998. Heat stability analysis of embankment on the degrading permafrost district in the East of the Tibetan Plateau, China. Cold Regions Science and Technology, 28(3): 183-188. DOI:10.1016/S0165-232X(98)00018-4 |
Li XW, Li XY. 1989. Wave propagation with mass-coupling effect in fluid-saturated porous media. Applied Mathematics and Mechanics, 10(4): 321-327. DOI:10.1007/BF02017772 |
Liu B, Su Q, Zhao WH, et al. 2017. Reflection and transmission of P waves at interfaces of saturated sandwiched coarse granular structure. Journal of Southwest Jiaotong University, 52(2): 280-287. DOI:10.3969/j.issn.0258-2724.2017.02.010 |
Liu ZJ, Xia TD, Zhang QF, et al. 2014. Parametric studies of propagation characteristics of bulk waves in two-phase porous media. Rock and Soil Mechanics, 35(12): 3443-3450. DOI:10.16285/j.rsm.2014.12.001 |
Lu HL. 2001. Continuum theory of mixture for freezing and thawing of water-saturated porous media. Journal of Southwest Jiaotong University, 36(6): 599-603. DOI:10.3969/j.issn.0258-2724.2001.06.011 |
Lu JF, Hanyga A. 2005. Linear dynamic model for porous media saturated by two immiscible fluids. International Journal of Solids and Structures, 42(9–10): 2689-2709. DOI:10.1016/j.ijsolstr.2004.09.032 |
Miao TD, Zhu JJ, Ding BY. 1995. Essay on constitutive relation of wave propagation in saturated porous media. Chinese Journal of Theoretical and Applied Mechanics, 27(5): 536-543. DOI:10.6052/0459-1879-1995-5-1995-464 |
Ming F, Zhang Y, Li DQ. 2016. Experimental and theoretical investigations into the formation of ice lenses in deformable porous media. Geosciences Journal, 20(5): 667-679. DOI:10.1007/s12303-016-0005-1 |
Van Genuchten. 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(44): 892-898. |
Vardoulakis I, Beskos DE. 1986. Dynamic behavior of nearly saturated porous media. Mechanics of Materials, 5(1): 87-108. DOI:10.1016/0167-6636(86)90017-7 |
Wei CF, Muraleetharan KK. 2006. Acoustical characterization of fluid-saturated porous media with local heterogeneities: theory and application. International Journal of Solids and Structures, 43(5): 982-1008. DOI:10.1016/j.ijsolstr.2005.06.008 |
Xu XT, Lai YM, Liu F, et al. 2011. A study of mechanical test methods of frozen soil. Journal of Glaciology and Geocryology, 33(5): 1132-1138. |
Yang SY, Yu MH. 2000. Constitutive descriptions of multiphase porous media. Acta Mechanica Sinica, 32(1): 11-24. DOI:10.3321/j.issn:0459-1879.2000.01.002 |
Zhou FX, Lai YM. 2011. Propagation characteristics of elastic wave in saturated frozen soil. Rock and Soil Mechanics, 32(9): 2669-2674. DOI:10.3969/j.issn.1000-7598.2011.09.018 |
Zhou XM, Sun MY, Xia TD, et al. 2008. Effect of the fluid on propagation characteristics of compressible waves in saturated soils. Journal of Harbin Institute of Technology, 40(6): 974-977. DOI:10.3321/j.issn:0367-6234.2008.06.031 |
 2018, Vol. 10
2018, Vol. 10
