Article Information
- JunPing Ren, Sai K. Vanapalli, Zhong Han . 2017.
- Soil freezing process and different expressions for the soil-freezing characteristic curve
- Sciences in Cold and Arid Regions, 9(3): 221-228
- http://dx.doi.org/10.3724/SP.J.1226.2017.00221
Article History
- Received: November 15, 2016
- Accepted: December 15, 2016
2. School of Civil Engineering, Wuhan University, Wuhan, Hubei 430072, China
The effects of harsh climate on geotechnical infrastructure in cold regions such as Canada, Northern United States and North-East Asia should be duly considered by designers and contractors (Bronfenbrener and Bronfenbrener, 2012). For example, in the Province of Quebec in Canada, with freezing indices ranging from 800 to over 2,000 degree-days, frost penetrates to a depth typically greater than 1.5 m. The frost action mainly develops in frost-susceptible soils, which leads to the formation of ice lens, surface heave, and eventual distress to the infrastructure (Konrad, 2005). In frozen soils, ice and unfrozen water coexist. Variation in the unfrozen water and ice contents significantly influences the physical and mechanical properties of frozen soils.
The relationship between the unfrozen water content and sub-freezing temperature or suction at ice-water interface is defined as the soil-freezing characteristic curve (SFCC). Since SFCC links the degree of phase transition to the sub-freezing temperature, the frozen soil properties, such as the segregation potential for frost heave, resilient modulus, and shear strength, can be interpreted using SFCC as a tool (Liu and Yu, 2014). For example, Azmatch et al. (2012b) predicted the hydraulic conductivity function of partially frozen Devon silt using SFCC, saturated hydraulic conductivity and empirical relationships developed by Fredlund et al. (1994) for estimating the hydraulic conductivity. Berg et al. (1996) conducted resilient modulus tests on several pavement materials from the Minnesota Road Research Project (Mn/ROAD) to characterize their behavior under seasonal frost conditions. The resilient modulus of pavement materials under frozen condition was expressed as a function of unfrozen water content, which is related to sub-freezing temperature by SFCC. Similarly, the strength of frozen soils can be predicted based on their unfrozen water content as per the study of Hivon and Sego (1995).
The SFCC has been recognized as a fundamental relationship in cold region engineering (Anderson and Morgenstern, 1973). Therefore, it is of critical importance to rigorously describe SFCC with reliable expressions. During the past decades, different equations and relationships have been proposed for SFCC (Kurylyk and Watanabe, 2013). They are either empirical relationships developed between the unfrozen water content and sub-freezing temperature or equations that exploit the similarity between SFCC and soil-water characteristic curve (SWCC), which correlates soils' water content to soil suction at air-water interface in unfrozen unsaturated soil. The soil freezing process and the similarity between SFCC and SWCC are reviewed in this paper. A conceptual SFCC is highlighted to illustrate the main characteristics of soil freezing and thawing. In addition, various SFCC expressions proposed in the literature are succinctly summarized. Amongst them, two empirical relationships and two equations were selected and evaluated by fitting the experimental data on four different soils ranging from coarse-grained soils to fine-grained soils. This study provides useful information of SFCC expressions for use in engineering practice in cold regions.
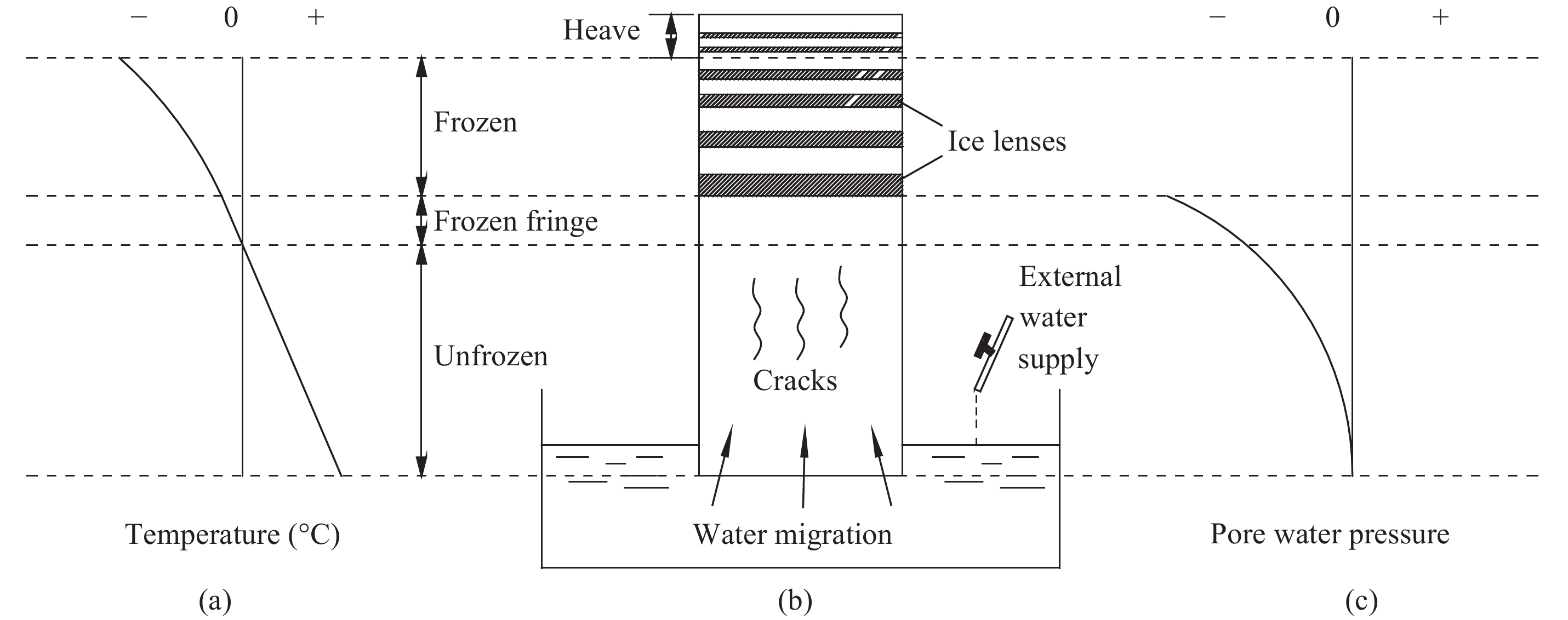
2 Soil freezing processFigure 1 shows the soil freezing process in an open system. When the air temperature is lower than the soil temperature, heat is extracted from the soil to the environment which results in a temperature profile as presented in Figure 1a. The freezing front (0 °C isotherm) progresses as a function of the imbalance associated with heat supplied to the heat removed as the pore-water freezes in situ (Konrad and Morgenstern, 1980). As the freezing front advances, the upper portion of the soil becomes frozen while the lower portion remains unfrozen. A partly frozen layer, namely the frozen fringe, exists between the frozen and unfrozen soil layers (Figure 1b). Thermodynamic processes occurring in the frozen fringe contribute to the generation of negative pore water pressure (or suction) (Williams, 1966; Konrad and Morgenstern, 1980), as presented in Figure 1c. As a result, hydraulic gradient develops and water migrates from the unfrozen soil to frozen soil.
Ice lenses will form if sufficient amount of water is accumulated behind the freezing front, resulting in soil mass heave (Figure 1b). The thickness and spacing of the ice lenses depend on the relative magnitudes of the rate of freezing and water availability (Penner, 1961). Near the surface, the temperature gradient is large, thus the rate of freezing is also high. However, the pore water does not have enough time to form thick ice lenses. Instead, thin ice lenses form with a relatively close spacing in this situation. As the freezing front penetrates to deeper soil layers, the rate of freezing is relatively low due to lower temperature gradient. In this case, there is enough time for water to migrate towards the freezing front from the lower unfrozen zone and to freeze. Therefore, thick ice lenses form. The non-uniform distribution of ice lenses in the soil mass contributes to the development of cracks which occur more frequently near the surface and decrease in frequency with increasing depth (Benson and Othman, 1993). These cracks pose a significant influence on the performance of different infrastructure constructed in frozen soils.
|
| Figure 1 Soil freezing in an open system: (a) temperature profile; (b) soil profile, water migration and ice lenses formation; and (c) negative pore water pressure (suction) profile (modified from Benson and Othman, 1993) |
In a frozen soil, unfrozen water and pore ice coexist. The principal factor determining the quantity of unfrozen water is temperature (Nersesova and Tsytovich, 1963). Pressure is a less important but a valid influencing factor. An increase in pressure increases the unfrozen water content at a given temperature. Besides, solute concentration, particle size distribution, chemical and mineralogical nature of the soil matrix also affect the unfrozen water content (Nersesova and Tsytovich, 1963; Anderson and Tice, 1973).
The relationship between unfrozen water content and sub-freezing temperature or negative pore water pressure (suction) in a frozen soil is characterized by SFCC (Koopmans and Miller, 1966; Spaans and Baker, 1996; Azmatch et al., 2012b ). The Clapeyron equation can be used to convert sub-freezing temperature to suction or vice versa with assumptions that (i) the pore ice pressure in a saturated frozen soil is equal to atmospheric pressure and (ii) the solute effect is negligible (Konrad and Morgenstern, 1980; Black and Tice, 1989). The equation is as follows (Azmatch et al., 2012b ; Kurylyk and Watanabe, 2013),
| $\psi = - L{\rho _w}\ln \frac{{T + 273.15}}{{{T_0} + 273.15}}$ | (1) |
where ψ is suction (kPa); L is latent heat of fusion of water (L = 334,000 J/kg); T is sub-freezing temperature (°C); T0 is normal freezing temperature (T0 = 0 °C); and ρw is water density (ρw = 1 g/cm3). The negative sign is used to achieve a positive value of suction, which is used in later SFCC equations. A decrease in soil temperature by 1 °C typically increases the suction by about 1,250 kPa (Zhou et al., 2014 ).
Equation (1) can be further simplified to Equation (2) since ln ((T+273.15)/(T0+273.15)) is approximately equal to T/(273.15) (Kurylyk and Watanabe, 2013),
| $\psi = - L{\rho _w}\frac{T}{{273.15}}$ | (2) |
Koopmans and Miller (1966) measured both SFCC and SWCC for three different soils and showed that SFCC is similar to SWCC. This is due to the similarity in physical processes experienced during drying and wetting in unfrozen unsaturated soil and freezing and thawing in saturated frozen soil. When soils are subjected to drying, water is gradually removed and replaced by air, leaving the remaining water at an increasingly lower potential. The physical process that occurs in freezing soils is similar, except that liquid water changes phase and becomes ice. The same forces that prevent soil water from draining also prevent it from freezing (Spaans and Baker, 1996). In other words, the temperature gradient in frozen soil can be considered to act in a manner similar to the potential gradient in an unfrozen soil (Zhou et al., 2014 ).
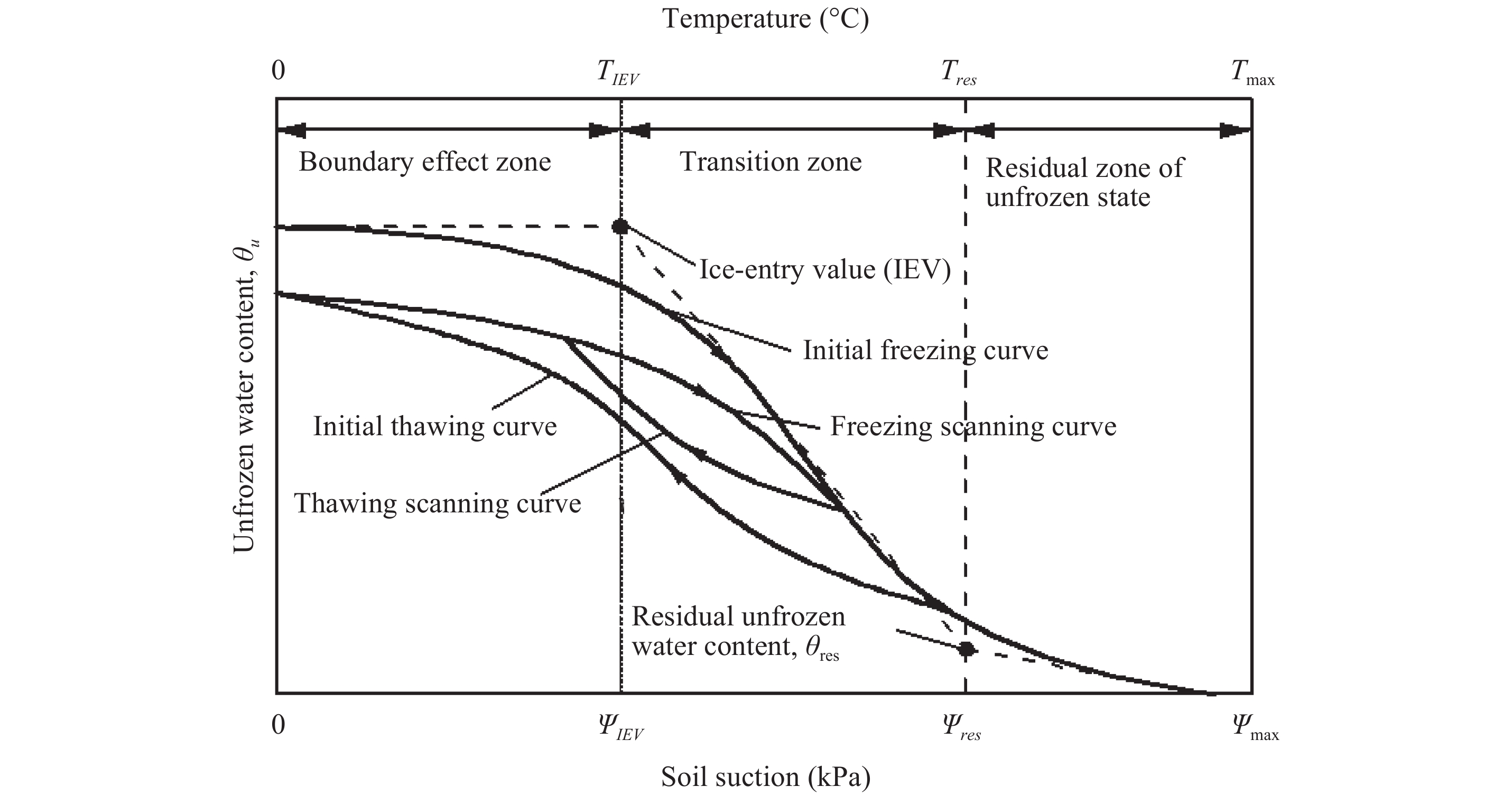
Based on their similarity, a conceptual SFCC can be drawn, as presented in Figure 2. Ice will form in the largest pores firstly when the temperature decreases (soil suction gradually increases). The corresponding suction or temperature at this stage is referred to as the ice-entry value (IEV) (Azmatch et al., 2012a ). The unfrozen water content in the soil gradually decreases along the freezing curve. At a certain sub-freezing temperature, most of the pore water turns into ice and beyond this temperature extremely low temperature (i.e., very high suction) would be required to further reduce the unfrozen water. This specific unfrozen water content is referred to as residual unfrozen water content. Similar to SWCC, SFCC could be divided into three zones, i.e., boundary effect zone (where no pore ice forms), transition zone (where sharp drop in the unfrozen water content is experienced), and residual zone of unfrozen state (where variation in the unfrozen water content is insignificant in spite of significant changes in temperature or suction). These characteristics are similar to descriptions provided for SWCC (Vanapalli et al., 1999 ). In addition, SFCC also shows hysteretic behavior (Koopmans and Miller, 1966) which is similar to SWCC. This can be attributed to several possible mechanisms such as the phenomenon of metastable nucleation, the effect of electrolyte, and pore blocking (Tian et al., 2014 ).
|
| Figure 2 Typical soil-freezing characteristic curve |
Several SFCC expressions are available in the literature. These expressions can be divided into two groups. The first group was based on empirical relationships between the unfrozen water content and sub-freezing temperature. The second group was developed by exploiting the similarity between SFCC and SWCC, with aid of the Clapeyron equation correlating the sub-freezing temperature to soil suction at the ice-water interface.
4.1 Empirical relationshipsAnderson and Tice (1972) found that unfrozen water content of most frozen soils can be conveniently expressed as a function of temperature by a simple power curve,
| ${\theta _u} = \frac{{{\rho _d}}}{{{\rho _w}}}\alpha {( - T)^\beta }$ | (3) |
where θu is volumetric unfrozen water content, ρd is dry density (g/cm3), α and β are model parameters.
Mckenzie et al. (2007) suggested an exponential function for the relationship between degree of saturation in frozen soil and temperature. Equation (4) can be used for estimating the volumetric unfrozen water content,
| ${\theta _u} = {\theta _{res}} + ({\theta _{sat}} - {\theta _{res}})\exp \left[ { - {{\left( {\frac{{T - {T_0}}}{\gamma }} \right)}^2}} \right]$ | (4) |
where θsat is volumetric unfrozen water content at saturated condition (θsat is equal to soil porosity), θres is residual volumetric unfrozen water content, and γ is model parameter.
Kozlowski (2007) developed a non-linear piecewise function for SFCC. It is expressed as:
| $\left\{ \begin{split}& {\theta _u} = {\theta _{sat}}\qquad\qquad\qquad\qquad\qquad \qquad\quad\!\!\!\!\!\!{\rm{for}}\,\,\,\,\, T > {T_0}\\& {\theta _u} = {\theta _{res}} + ({\theta _{sat}} - {\theta _{res}})\exp \left[ {\delta {{\left( \displaystyle {\frac{{{T_0} - T}}{{T - {T_{res}}}}} \right)}^\varepsilon }} \right]{\rm{for}}\,\,\,\,\, {T_{res}} < T \le {T_0}\\& {\theta _u} = {\theta _{res}}\qquad\qquad\qquad\qquad\qquad \qquad\quad\!\!\!\!\!\!{\rm{for}}\,\,\,\,\, T \le {T_{res}}\end{split} \right.$ | (5) |
where Tres is temperature corresponding to θres (°C), δ and ε are model parameters.
In addition to the power, exponential and non-linear piecewise relationships, simple linear piecewise relationships can also be used to reasonably approximate SFCC (McKenzie et al., 2007 ; Kurylyk and Watanabe, 2013).
4.2 Relationship based on similarity between SFCC and SWCCThe SFCC is derived from SWCC by relating suction with sub-freezing temperature, through the Clapeyron equation (Dall'Amico, 2010). Different SWCC equations, such as those proposed by Brooks and Corey (1964), van Genuchten (1980) and Fredlund and Xing (1994), have been used as SFCC equations by replacing suction at the air-water interface in unsaturated unfrozen soil with suction at the ice-water interface in saturated frozen soil (e.g., Shoop and Bigl, 1997; Dall'Amico, 2010; Sheshukov and Nieber, 2011; Azmatch et al., 2012b ).
By combining the simplified Clapeyron equation (Equation (2)) with the Brooks and Corey (1964) equation, Sheshukov and Nieber (2011) obtained a relationship for unfrozen water content and sub-freezing temperature,
| ${\theta _u} = {\theta _{res}} + ({\theta _{sat}} - {\theta _{res}}){\left( {\frac{{ - 1}}{{{\psi _{IEV}}}}\frac{{L{\rho _w}T}}{{273.15}}} \right)^{ - 1/b}}$ | (6) |
where ψIEV is ice-entry value (kPa), and b is the Brooks and Corey (1964) SWCC model parameter.
Zhang et al. (2016) incorporated the Clapeyron equation (Equation (1)) into the van Genuchten (1980) SWCC equation and proposed the following SFCC relationship,
| ${\theta _u} \!=\! {\theta _{res}} \!+\! ({\theta _{sat}} \!-\! {\theta _{res}}){\left[ {1 \!+\! {{\left( {{a_{vg}}L{\rho _w}\ln \frac{{T \!+\! 273.15}}{{{T_0} \!+\! 273.15}}} \right)}^{{n_{vg}}}}} \right]^{ - {m_{vg}}}}$ | (7) |
where avg, nvg, and mvg are the van Genuchten (1980) SWCC model parameters.
Azmatch et al. (2012b) showed that the Fredlund and Xing (1994) equation can reasonably approximate SFCC when replacing suction at the air-water interface by suction at the ice-water interface. By employing Equation (1), the SFCC can be expressed as:
| ${\theta _u} = \frac{{{\theta _{sat}}}}{{{{\left\{ \displaystyle{\ln \left[ {{\rm{2}}.{\rm{718}} + {{\left( {\frac{{L{\rho _w}}}{{{a_f}}}\ln \left( {\frac{{T + 273.15}}{{{T_0} + 273.15}}} \right)} \right)}^{{n_f}}}} \right]} \right\}}^{{m_f}}}}}$ | (8) |
where af, nf, and mf are the Fredlund and Xing (1994) SWCC model parameters.
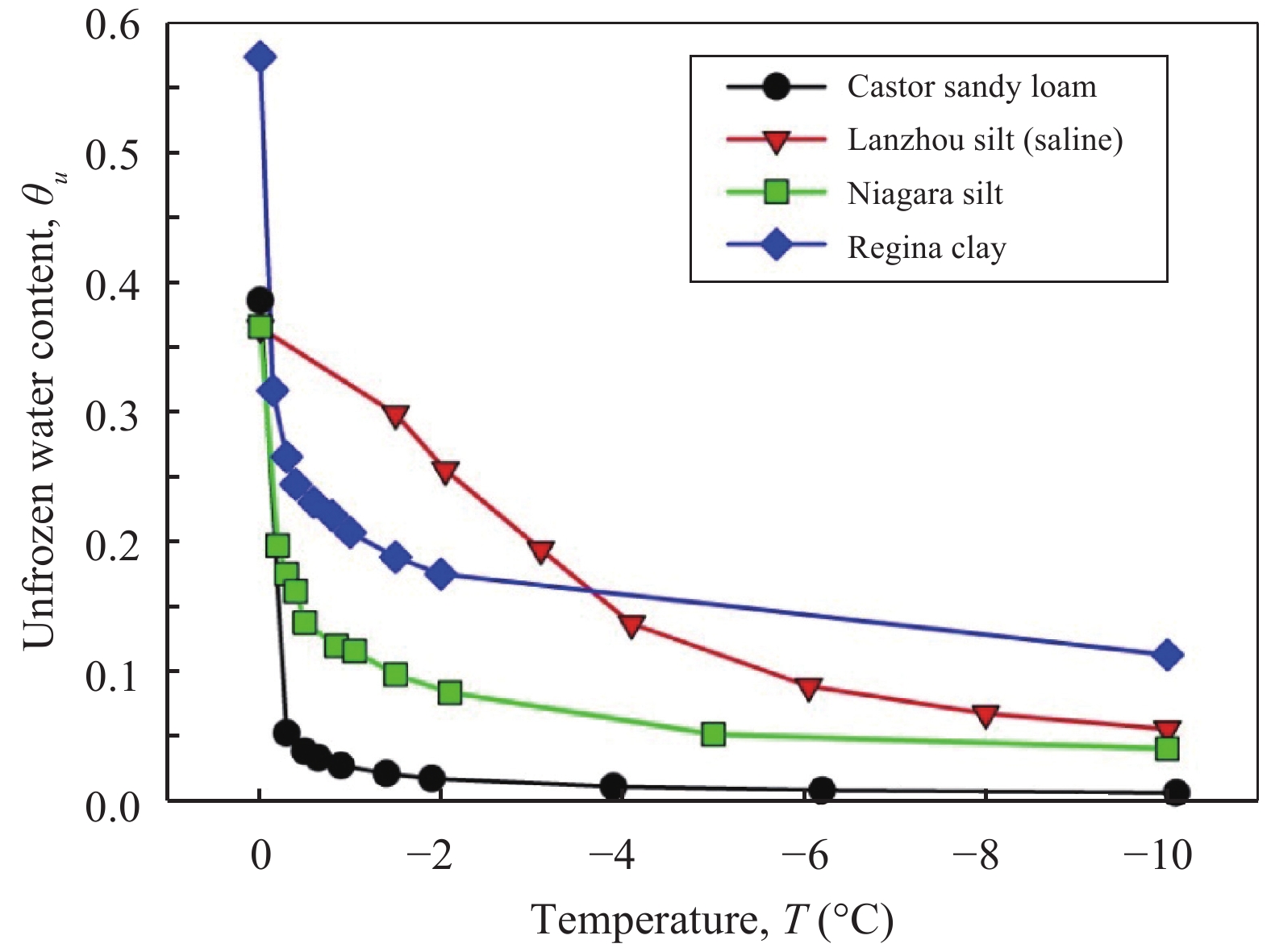
5 Comparison of different soil-freezing characteristic curve expressions and discussionFour different expressions, namely, the power relationship (Equation (3)), exponential relationship (Equation (4)), van Genuchten equation (Equation (7)), and Fredlund and Xing equation Equation (8)), were chosen to fit the measured SFCC data. Four soils from the literature (Smith and Tice, 1988) were used for providing comparisons between measured and best-fitted SFCCs. The four soils were saturated with distilled water and the volumetric unfrozen water contents were measured using time domain reflectometry (TDR), which is widely used for measuring unfrozen water content in frozen soils. The basic properties of the four soils are summarized in Table 1. Figure 3 shows the SFCCs for these soils. The residual unfrozen water content was determined by extending the linear transition zone to intersect a linear extension of the residual zone of unfrozen state, following procedure summarized in Vanapalli et al. (1999) (Figure 2).
| Soil | Dry density (g/cm3) | Saturated unfrozen water content θsat | Residual unfrozen water content θres | Specific surface area (m2/g) |
| Castor sandy loam | 1.475 | 0.385 | 0.020 | — |
| Lanzhou silt (saline) | 1.655 | 0.364 | 0.100 | 34 |
| Niagara silt | 1.645 | 0.365 | 0.091 | 37 |
| Regina clay | 0.961 | 0.572 | 0.190 | 291 |
|
| Figure 3 SFCC of the studied soils |
It can be seen from Figure 3 that the SFCCs of different soils show similar trends in their variation. The unfrozen water content decreases significantly as temperature drops from 0 °C to −2 °C, after which it gradually becomes constant. Regina clay has much higher unfrozen water content than Niagara silt and Castor sandy loam at lower temperatures. This can be attributed to the reason that Regina clay is higher in finer size particles which can adsorb more water on their surface, resulting in higher unfrozen water content even when the temperature drops below −10 °C. When soil pore water contains salinity, SFCC is different from that of soil in which salinity is absent. As an example, unfrozen water content of the saline Lanzhou silt does not show dramatic reduction when the temperature drops to −2 °C, and the slope of the freezing curve is much smaller than that of Niagara silt, although both of these soils are silty soils and have approximately the same specific surface area.
The selected SFCC relationships and equations were used to fit the measured volumetric unfrozen water contents and the results are summarized in Table 2 and Figure 4.
| Power relationship | Exponential relationship | van Genuchten (1980) | Fredlund and Xing (1994) | |||||||||||||
| α | β | R2 | γ | R2 | avg | nvg | mvg | R2 | af | nf | mf | R2 | ||||
| Castor sandy loam | 0.018 | −0.583 | 1.00 | 0.194 | 0.99 | 0.013 | 3.369 | 0.449 | 0.99 | 80.6 | 2.541 | 1.423 | 1.00 | |||
| Lanzhou silt (saline) | 0.116 | −0.152 | 0.53 | 2.909 | 0.96 | 0.0002 | 2.374 | 2.845 | 0.96 | 2,933.5 | 2.130 | 1.648 | 0.99 | |||
| Niagara silt | 0.070 | −0.256 | 0.96 | 0.268 | 0.86 | 0.002 | 1.044 | 2.095 | 0.93 | 119.0 | 1.071 | 1.231 | 0.99 | |||
| Regina clay | 0.212 | −0.224 | 0.99 | 0.150 | 0.88 | 0.012 | 1.769 | 0.666 | 0.93 | 50.9 | 1.600 | 0.650 | 0.99 | |||

|
| Figure 4 Comparison between measured and best-fit SFCCs for (a) Castor sandy loam; (b) Lanzhou silt; (c) Niagara silt and (d) Regina clay |
Figure 4 shows comparisons between measured and fitted SFCCs for the four soils. All four relationships/equations used in the present study can reasonably fit the measured SFCCs of soils without salinity. The measured data of Castor sandy loam is well fitted by the four expressions. However, the exponential relationship and van Genuchten equation are less accurate than the power relationship and Fredlund and Xing equation for Niagara silt and Regina clay. The reason is that for the exponential relationship and van Genuchten equation, the minimum value of unfrozen water content is limited by the residual unfrozen water content (θres). In other words, the minimum value of the predicted unfrozen water content is equal to θres if these two expressions are employed. As can be seen from Figures 3 and 4, the unfrozen water content of Castor sandy loam levels off after −2 °C, but the unfrozen water contents of Niagara silt and Regina clay still decrease with a relatively lower rate, due to their relatively small particle sizes and large surface area. This implies that the θres can be well defined for the sandy loam compared to the silt and clay.
The exponential relationship and Fredlund and Xing equation are able to provide good fit for the saline Lanzhou silt. On the contrary, the power relationship is not as accurate as it is for other three soils. For giving reasonable fitting for SFCC of saline silt, the parameter avg of the van Genuchten equation was fixed to 0.0002. Of all the various expressions used in the present study, the Fredlund and Xing equation is able to provide suitable fittings for all the four soils, including the saline soil.
In summary, the exponential relationship seems to be a good choice for sands and sandy soils whose unfrozen water content drops dramatically with temperature slightly below 0 °C and levels off afterwards. The power relationship provides good fits for sandy loam, silt, and clay; however, for the saline silt studied, only a fair fit was achieved. The power and exponential relationships are empirical but simple, and they are smooth and can be easily differentiated for determining the apparent heat capacity (McKenzie et al., 2007 ). On the contrary, the van Genuchten and Fredlund and Xing equations are relatively complex and require the Clapeyron equation, which is valid when thermodynamic equilibrium has been achieved. Moreover, the assumptions on which the Clapeyron equation is based need further investigations for employing them for SFCC equations. The exponential relationship and the van Genuchten equation are more suitable for sandy soils in comparison to silt or clay. The Fredlund and Xing equation well fitted the SFCCs for all four soils, showing higher flexibility for use on soils with different particle sizes.
6 ConclusionsThe variations in unfrozen water and ice contents with changes in temperature significantly influence the physical and mechanical properties of frozen soils. A SFCC is required to understand the flow of heat, water, and solute in frozen soils (Spaans and Baker, 1996). A succinct review of the soil freezing process and the similarity between SFCC and SWCC is provided in this paper. A conceptual SFCC is drawn to illustrate key features of soil freezing and thawing. Four SFCC expressions (i.e., two empirical relationships and two equations based on the similarity between SFCC and SWCC) were selected for providing comparisons between the measured and fitted unfrozen water contents for four different soil types. The results suggest that the exponential relationship and van Genuchten equation are more suitable for sandy soils. The power relationship could reasonably fit SFCC for soils with different particle sizes, but not for saline silt. The Fredlund and Xing equation provides good fits for all four soils investigated in the present study, showing its flexibility for different soil types. However, more efforts should be put into investigating the theoretical background for employing the Clapeyron equation and the similarity between SFCC and SWCC for predicting the unfrozen water contents.
Acknowledgments:The authors gratefully acknowledge the sponsorships from the China Scholarship Council (CSC)-University of Ottawa joint scholarship, the Natural Sciences and Engineering Research Council of Canada (NSERC), and the Ministry of Transportation of Ontario (MTO).
| Anderson DM, Morgenstern NR, 1973. Physics, chemistry, and mechanics of frozen ground: a review. In Permafrost: The North American Contribution to the Second International Conference, National Academy of Sciences, Washington DC, pp. 257–288. |
| Anderson DM, Tice AR, 1972. Predicting unfrozen water contents in frozen soils from surface area measurements. Highway Research Record, 393: 12–18. |
| Anderson DM, Tice AR, 1973. The unfrozen interfacial phase in frozen soil water systems. In: Hadas A, Swartzendruber D, Rijtema PE, et al. (eds.). Springer Berlin Heidelberg, pp. 107–124. |
| Azmatch TF, Sego DC, Arenson LU, et al., 2012a. New ice lens initiation condition for frost heave in fine-grained soils. Cold Regions Science and Technology, 82: 8–13. DOI: 10.1016/j.coldregions. 2012.05.003. |
| Azmatch TF, Sego DC, Arenson LU, et al., 2012b. Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils. Cold Regions Science and Technology, 83: 103–109. DOI: 10.1016/j.coldregions.2012.07.002. |
| Benson CH, Othman MA, 1993. Hydraulic conductivity of compacted clay frozen and thawed in situ. Journal of Geotechnical Engineering, 119(2): 276–294. DOI: 10.1061/(ASCE)0733–9410(1993)119:2(276) |
| Berg RL, Bigl SR, Stark J, et al., 1996. Resilient modulus testing of materials from Mn/ROAD, Phase 1. USA Cold Regions Research and Engineering Laboratory, Special Report 96–19, Mn/DOT Report 96–21. |
| Black PB, Tice AR, 1989. Comparison of soil freezing curve and soil water curve data for Windsor sandy loam. Water Resources Research, 25(10): 2205–2210. DOI: 10.1029/WR025i010p02205 |
| Bronfenbrener L, Bronfenbrener R, 2012. A temperature behavior of frozen soils: Field experiments and numerical solution. Cold Regions Science and Technology, 79: 84–91. DOI: 10.1016/j.coldregions.2012.03.005 |
| Brooks RH, Corey AT, 1964. Hydraulic properties of porous media. Transactions of the ASAE, 7(1): 1–27. DOI: 10.13031/2013.40684 |
| Dall'Amico M, 2010. Coupled water and heat transfer in permafrost modeling. Ph.D. Thesis, University of Trento, pp. 43. |
| Fredlund DG, Xing A, 1994. Equations for the soil-water characteristic curve. Canadian Geotechnical Journal, 31(4): 521–532. DOI: 10.1139/t94–061 |
| Fredlund DG, Xing A, Huang S, 1994. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Canadian Geotechnical Journal, 31(4): 533–546. DOI: 10.1139/t94-062 |
| Hivon EG, Sego DC, 1995. Strength of frozen saline soils. Canadian Geotechnical Journal, 32(2): 336–354. DOI: 10.1139/t95-034 |
| Konrad JM, 2005. Estimation of the segregation potential of fine-grained soils using the frost heave response of two reference soils. Canadian Geotechnical Journal, 42(1): 38–50. DOI: 10.1139/t04-080 |
| Konrad JM, Morgenstern NR, 1980. A mechanistic theory of ice lens formation in fine-grained soils. Canadian Geotechnical Journal, 17(4): 473–486. DOI: 10.1139/t80-056 |
| Koopmans RWR, Miller RD, 1966. Soil freezing and soil water characteristic curves. Soil Science Society of America Journal, 30(6): 680–685. DOI: 10.2136/sssaj1966.03615995003000060011x |
| Kozlowski T, 2007. A semi-empirical model for phase composition of water in clay-water systems. Cold Regions Science and Technology, 49(3): 226–236. DOI: 10.1016/j.coldregions.2007.03.013 |
| Kurylyk BL, Watanabe K, 2013. The mathematical representation of freezing and thawing processes in variably-saturated, non-deformable soils. Advances in Water Resources, 60: 160–177. DOI: 10.1016/j.advwatres.2013.07.016 |
| Liu Z, Yu X, 2014. Predicting the phase composition curve in frozen soils using index properties: A physic-empirical approach. Cold Regions Science and Technology, 108: 10–17. DOI: 10.1016/j.coldregions.2014.09.003 |
| McKenzie JM, Voss CI, Siegel DI, 2007. Groundwater flow with energy transport and water-ice phase change: numerical simulations, benchmarks, and application to freezing in peat bogs. Advances in Water Resources, 30(4): 966–983. DOI: 10.1016/j.advwatres.2006.08.008 |
| Nersesova ZA, Tsytovich NA, 1963. Unfrozen water in frozen soils. In: Permafrost: Proceedings of 1st International Conference, pp. 11–15. |
| Penner E, 1961. The importance of freezing rate in frost action in soils. Proceedings of the American Society for Testing and Materials, 60: 1151–1165. |
| Sheshukov AY, Nieber JL, 2011. One-dimensional freezing of nonheaving unsaturated soils: Model formulation and similarity solution. Water Resources Research, 47(11): W11519. DOI: 10.1029/2011WR010512 |
| Shoop SA, Bigl SR, 1997. Moisture migration during freeze and thaw of unsaturated soils: modeling and large scale experiments. Cold Regions Science and Technology, 25(1): 33–45. DOI: 10.1016/S0165-232X(96)00015-8 |
| Smith MW, Tice AR, 1988. Measurement of the unfrozen water content of soils—comparison of nmr (nuclear magnetic resonance) and tdr (time domain reflectometry) methods. No. CRREL-88-18. Cold Regions Research and Engineering Lab, Hanover, NH. |
| Spaans EJ, Baker JM, 1996. The soil freezing characteristic: its measurement and similarity to the soil moisture characteristic. Soil Science Society of America Journal, 60: 13–19. DOI: 10.2136/sssaj1996.03615995006000010005x |
| Tian H, Wei C, Wei H, et al, 2014. Freezing and thawing characteristics of frozen soils: Bound water content and hysteresis phenomenon. Cold Regions Science and Technology, 103: 74–81. DOI: 10.1016/j.coldregions.2014.03.007 |
| Vanapalli SK, Fredlund DG, Pufahl DE, 1999. The influence of soil structure and stress history on the soil-water characteristics of a compacted till. Géotechnique, 49(2): 143–159. DOI: 10.1680/geot.1999.49.2.143 |
| van Genuchten MT, 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5): 892–898. DOI: 10.2136/sssaj1980.03615995004400050002x |
| Williams PJ, 1966. Pore pressures at a penetrating frost line and their prediction. Géotechnique, 16(3): 187–208. DOI: 10.1680/geot.1966.16.3.187 |
| Zhang S, Teng J, He Z, et al, 2016. Importance of vapor flow in unsaturated freezing soil: a numerical study. Cold Regions Science and Technology, 126: 1–9. DOI: 10.1016/j.coldregions.2016.02.011 |
| Zhou X, Zhou J, Kinzelbach W, et al, 2014. Simultaneous measurement of unfrozen water content and ice content in frozen soil using gamma ray attenuation and TDR. Water Resources Research, 50(12): 9630–9655. DOI: 10.1002/2014WR015640 |
 2017, 9
2017, 9


