Article Information
- HeQiang Du, Tao Wang, Xian Xue . 2017.
- Field determination for roughness length above the different non-erodible surfaces
- Sciences in Cold and Arid Regions, 9(1): 67-77
- http://dx.doi.org/10.3724/SP.J.1226.2017.00067
Article History
- Received: August 23, 2016
- Accepted: October 30, 2016
Wind erosion is a major environmental problem in arid and semi-arid regions around the world that support about one-sixth of the world's population (Skidmore, 2000). For reducing or controlling wind erosion by non-erodible elements including wind immobile clasts and vegetation have long been recognized by agriculturists, in arid or semi-arid regions, thus blown sand protection systems composed of various non-erodible elements were built (Riksen et al., 2003; Qiu et al., 2004). The protective effect is affected by the varying geometry, spatial organization and density of the non-erodible elements. Aerodynamic roughness length is an important parameter in modern fluid mechanics, and it represents the interaction between surface and atmosphere, and reflects the reducing effect of wind speed by the surface (Raupach, 1992; Shao, 2001). Based on the conception of aerodynamic roughness length, it can be used to assess the protection effectiveness of non-erodible elements against wind erosion (Abtew et al., 1989; Lee, 1991). Under thermally neutral conditions, the roughness length is a characteristic measure of wind field stress caused by non-erodible roughness elements. Many scholars have used the aerodynamically derived roughness length to characterize the excess momentum extracted from the wind field by upwind roughness elements (Brutsaert, 1982; Lee, 1990; MacKinnon et al., 1990; Wolfe, 1993; Wolfe and Nickling, 1996). Previously, most scientists considered roughness length as a geometric parameter that is determined by the structure and formation of surface roughness elements (Lettau, 1969; Dickinson et al., 1997), and is often regarded as a constant or seasonally variable for certain typical surfaces (Sellers et al., 1986; Dickinson et al., 1997). However, even on the same surface, airflow will significantly change the structure and formation of flexible roughness elements, which affect the magnitude of roughness length. Therefore, roughness length is not a geometric parameter, but essentially a dynamic parameter (Zhou et al., 2006). It not only depends on the structure and formation of surface roughness elements, but also to some degree on near-surface airflow conditions (Monteith, 1973).
This paper derived the roughness lengths of five types of non-erodible surfaces including gravel, wheat straw checkerboard barriers surface, cotton stem checkerboard barriers surface, shrub surfaces, and herb surfaces by observational data, and focused on the variation of roughness length with wind velocity and characters of non-erodible elements. We hope this study would give some suggestions for defining the relationships among wind velocity, roughness length, wind velocity and characters of non-erodible elements.
2 Materials and method 2.1 Experiment site descriptionThe roughness lengths of the ground surface with gravel, checkerboards, and vegetation were studied, respectively. The experiment sites were mainly set-up in three regions. Surfaces with gravel, wheat straw checkerboards and cotton stems checkerboards were located on the roof of Mogao Grottoes in Dunhuang city, China (Figure 1). These three types of non-erodible surfaces belong to parts of the blown sand protection system of Mogao Grottoes. The experiment sites with vegetative surfaces were located in the Ulanbuht and Kubuqi deserts, China (Figure 1).
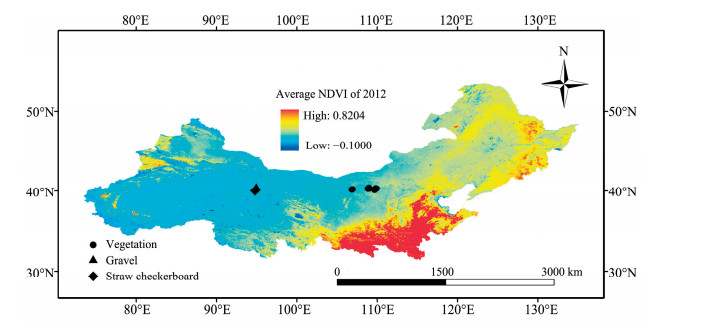
|
| Figure 1 Wind speed observed sites of nonerodible surfaces |
Surface gravel has an average diameter of 0.025 m, and coverage of 35%. The wheat straw checkerboards with 1m×1m grids, have an average height of 0.3 m above the ground. The central part inside the checkerboard is about 10 cm lower than the ground surface caused by long time wind erosion. On the cotton stem checkerboard surface, the size of checkerboards is 0.5m×0.5m, the average height is 0.25 m above the ground surface, and the central part inside the checkerboards is 11 cm lower than the ground surface. The concave surfaces are fully developed inside both the wheat and cotton straw checkerboards.
On the vegetative surfaces, six sites with herbs and 13 sites with shrub were selected. The sample plot surveys were used to obtain measurements of height (h), separation (s), and width (w) of vegetation in different sites. The image processing method was used to obtain frontal area (λ) and coverage (c) of vegetation. Digital photographs of the vegetation in quadrats in different directions and at different heights were digitized using the ERDAS IMAGING 9.1 image processing software to determine the differences in gray tone between the vegetation and the interstices between the vegetation. Then, vegetation and interstices were classified using an unsupervised classification method. Based on the fraction of pixels occupied by vegetation, the frontal area (λ) and coverage (c) of every quadrat were calculated (Du et al., 2014). The measured parameters of vegetative parameters are presented in Table 1.
| Vegetation type |
Site number |
Species | Height (m) |
Separation (m) |
Width (m) |
Coverage (%) |
Frontal area |
| Herb | Ⅰ-1 | Achnatherum splendens | 0.778 | 1.023 | 0.652 | 14.3 | 0.136 |
| Ⅰ-2 | Achnatherum splendens | 0.912 | 0.031 | 0.936 | 100.0 | 1.049 | |
| Ⅰ-3 | Agropyron cristatum | 0.498 | 0.231 | 0.003 | 16.2 | 0.205 | |
| Ⅰ-4 | Agropyron cristatum | 0.050 | 0.042 | 0.001 | 16.5 | 0.171 | |
| Ⅰ-5 | Agropyron cristatum | 0.150 | 0.043 | 0.001 | 13.8 | 0.144 | |
| Ⅰ-6 | Agropyron cristatum and Achnatherum splendens | 0.187 | 0.156 | 0.204 | 17.7 | 0.222 | |
| Shrub | Ⅱ-1 | Haloxylon ammodendron | 1.784 | 5.234 | 1.814 | 15.3 | 0.254 |
| Ⅱ-2 | Haloxylon ammodendron | 1.195 | 7.236 | 1.072 | 13.4 | 0.194 | |
| Ⅱ-3 | Seriphidium terrae-albae | 0.618 | 2.562 | 0.907 | 15.3 | 0.253 | |
| Ⅱ-4 | Seriphidium terrae-albae | 0.540 | 2.231 | 0.576 | 16.7 | 0.274 | |
| Ⅱ-5 | Seriphidium terrae-albae | 0.715 | 2.456 | 1.198 | 16.5 | 0.281 | |
| Ⅱ-6 | Seriphidium terrae-albae | 0.640 | 2.231 | 0.897 | 15.8 | 0.276 | |
| Ⅱ-7 | Seriphidium terrae-albae | 0.587 | 2.245 | 0.827 | 12.7 | 0.269 | |
| Ⅱ-8 | Artemisia ordosica | 0.643 | 1.423 | 0.831 | 18.9 | 0.301 | |
| Ⅱ-9 | Artemisia ordosica | 0.560 | 2.441 | 0.906 | 16.7 | 0.255 | |
| Ⅱ-10 | Artemisia ordosica | 0.313 | 2.325 | 0.530 | 12.8 | 0.208 | |
| Ⅱ-11 | Artemisia ordosica | 0.495 | 2.234 | 0.719 | 16.2 | 0.253 | |
| Ⅱ-12 | Artemisia ordosica | 0.497 | 2.569 | 0.869 | 13.7 | 0.218 | |
| Ⅱ-13 | Salix integra and Seriphidium terrae-albae | 1.029 | 2.841 | 0.991 | 14.2 | 0.234 |
Wind velocities on different non-erodible surfaces were measured using a mobile anemobiagraph station produced by MetOne Inc., America, which includes one wind direction sensor (024A) and eight wind velocity sensors (014A) operating at one-minute intervals. The wind direction sensors were placed at a height of 2.0 m, and the wind velocity sensors were installed at heights of 0.1, 0.2, 0.3, 0.4, 0.5, 1.0, 1.5, and 2.0 m above the surface. The mobile anemobiagraph station was set on the central part of the observed site during every observation. The observations were usually carried out in daytime (from 08:00 to 18:00). Every observation had three repetitions lasting 8 hours. The function of wind profile of every observation above different surfaces was fit, and ones with the logarithmic of R2 > 0.9 at 0.05 confidence level were chosen to make sure the measurements were under thermally neutral atmospheric conditions.
2.3 Calculation methodThe traditional method for calculating roughness length of the surface is the aerodynamically derived method, based on wind velocity measurements during thermally neutral atmospheric conditions (Brutsaert, 1982). When the atmospheric stability is neutral, the wind profile follows a logarithmic function and can be written as:
| $ {u_z} = \frac{{{u_*}}}{k}\ln \left({\frac{z}{{{z_0}}}} \right) $ | (1) |
where, z0 is the aerodynamic roughness length m; uz is the wind velocity, at height of z, m/s; u* is the friction velocity, m/s; k is Von Karman's constant, 0.4; z is measurement height, m; and d is the zero-plane displacement.
According to wind profile function, roughness length is defined as the height above the surface at which the wind velocity would drop to zero if the logarithmic profile is extrapolated down into the interfacial sub-layer. In the calculation, the zero-plane displacement can be assumed to be zero for the observation taken in the windy season, when the vegetation cover rarely exceeds 20% (Hoffmann et al., 2008). Thus, Equation (1) can be written as:
| $ {u_z} = \frac{{{u_*}}}{k}\ln (z) - \frac{{{u_*}}}{k}\ln ({z_0}) $ | (2) |
Taking u*/k as the slope and -u* ln (z0)/k as the intercept, Equation (2) can be written as a linear function which takes ln (z) as an independent value:
| $ {u_z} = a\ln (z) + b $ | (3) |
where, a and b are the fitting coefficients of the wind profile determined using observed data. By fitting Equation (2) using the observed data, wind profile equations for various surface can be obtained. The transform from Equation (2) to Equation (3) is sometimes sensitive to measurement error, causing invalid consequences (Liu and Dong, 2002). To eliminate this measurement error, in this study, the wind speed data where determination coefficient R2 of wind profile logarithmic function fitting are larger than 0.9 were selected to calculate the roughness length. Based on the concept of roughness length, when uz=0, z=z0. Therefore, the roughness length z0 can be calculated as:
| $ {z_0} = {e^{ - b/a}} $ | (4) |
Based on the calculated results, the relationships among vegetation conditions (vegetation cover and height), wind speed, and roughness length were analyzed using the method of correlation analysis, regression analysis.
3 Results 3.1 Roughness lengths on different nonerodible element surfacesAccording to field observations, the average roughness lengths of the different surfaces were obtained (Table 2). Table 2 shows that the roughness lengths vary with coverage and height of the roughness elements. Thus, two-way analysis of variance was carried out by SPSS 19.0 software (IBM Company, US) to determine if there was a significant effect of coverage and height of non-erodible elements on roughness length (Table 3). Table 3 shows that the corrected model has statistical significance at 95% confidence levels, for the P values are less than 0.005. This suggests that the coverage and height of non-erodible elements could significantly impact the roughness length. In the following text, we discuss the roughness lengths of the different surfaces.
| Non-erodible elements | Coverage (%) | Height of non-erodible element (m) |
Roughness length (m) |
| Gravel | 35 | 0.025 | 0.00056 |
| Wheat straw checkerboards | - | 0.300 | 0.01145 |
| Cotton stem checkerboards | - | 0.250 | 0.00042 |
| Achnatherum splendens | 14.3 | 0.778 | 0.00511 |
| Achnatherum splendens | 100 | 0.912 | 0.06880 |
| Agropyron cristatum | 16.2 | 0.498 | 0.00330 |
| Agropyron cristatum | 16.5 | 0.050 | 0.00400 |
| Agropyron cristatum | 13.8 | 0.150 | 0.00620 |
| Agropyron cristatum and Achnatherum splendens | 17.7 | 0.187 | 0.00880 |
| Haloxylon ammodendron | 15.3 | 1.784 | 0.01710 |
| Haloxylon ammodendron | 13.4 | 1.195 | 0.01293 |
| Seriphidium terrae-albae | 15.3 | 0.618 | 0.01040 |
| Seriphidium terrae-albae | 16.7 | 0.540 | 0.03770 |
| Seriphidium terrae-albae | 16.5 | 0.715 | 0.04750 |
| Seriphidium terrae-albae | 15.8 | 0.640 | 0.01770 |
| Seriphidium terrae-albae | 12.7 | 0.587 | 0.00400 |
| Artemisia ordosica | 18.9 | 0.643 | 0.04450 |
| Artemisia ordosica | 16.7 | 0.560 | 0.02130 |
| Artemisia ordosica | 12.8 | 0.313 | 0.00260 |
| Artemisia ordosica | 16.2 | 0.495 | 0.02350 |
| Artemisia ordosica | 13.7 | 0.497 | 0.01020 |
| Salix integra and Seriphidium terrae-albae | 14.2 | 1.029 | 0.02230 |
| Source | Type Ⅲ sum of squares |
df | Mean square | F | P values |
| Corrected model | 1.028a | 21 | 0.049 | 371.508 | 0.000 |
| Intercept | 0.940 | 1 | 0.940 | 7, 132.440 | 0.000 |
| Coverage | 0.178 | 3 | 0.059 | 450.384 | 0.000 |
| Height | 0.229 | 6 | 0.038 | 289.047 | 0.000 |
| Adjusted R2 | 0.727 | ||||
The roughness lengths in different wind velocity ranges on the gravel beds were calculated (Figure 2). The roughness length in the wind velocity range of 2~4 m/s is nearly zero, and increases with wind velocity. The increase rate in the wind velocity range of 6~7 m/s is much larger than the other wind velocity ranges.
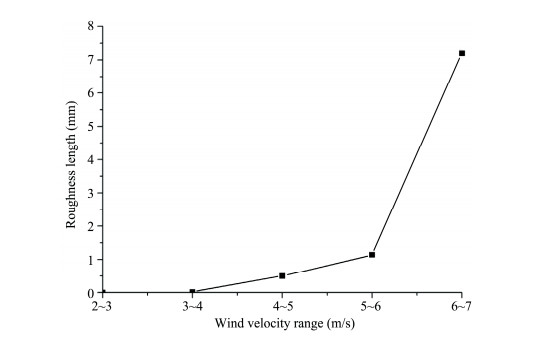
|
| Figure 2 Roughness lengths in different wind velocity ranges on the gravel bed |
Figure 3 displays the roughness lengths on surfaces covered by checkerboard sand barriers. The roughness lengths on both surfaces increase with wind velocity, and the increasing curves are approximately parallel.
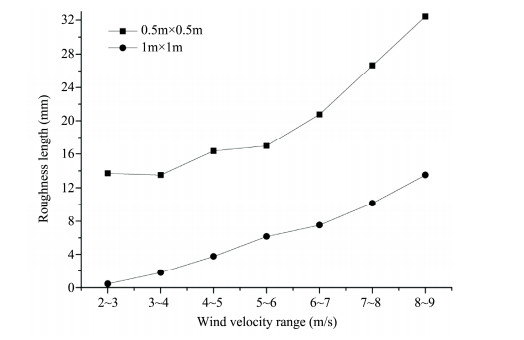
|
| Figure 3 Roughness lengths on the surfaces covered by checkerboard sand barriers (squares denotes checkerboard sand barriers with 0.5m×0.5m grids made of cotton stem; circles denotes 1m×1m grids made of wheat straw) |
The surface covered by barriers with the smaller grids generated the larger roughness length. The increasing forms of the roughness lengths on both surface have a small difference: the roughness length of the surface covered by the barriers with 0.5m×0.5m grids increases slowly in the wind velocity range of 2~6 m/s, and then increases quickly in the wind velocity range of 6~9 m/s. On the surface having 1m×1m grids, roughness length increases with wind velocity approximately in a linear relationship.
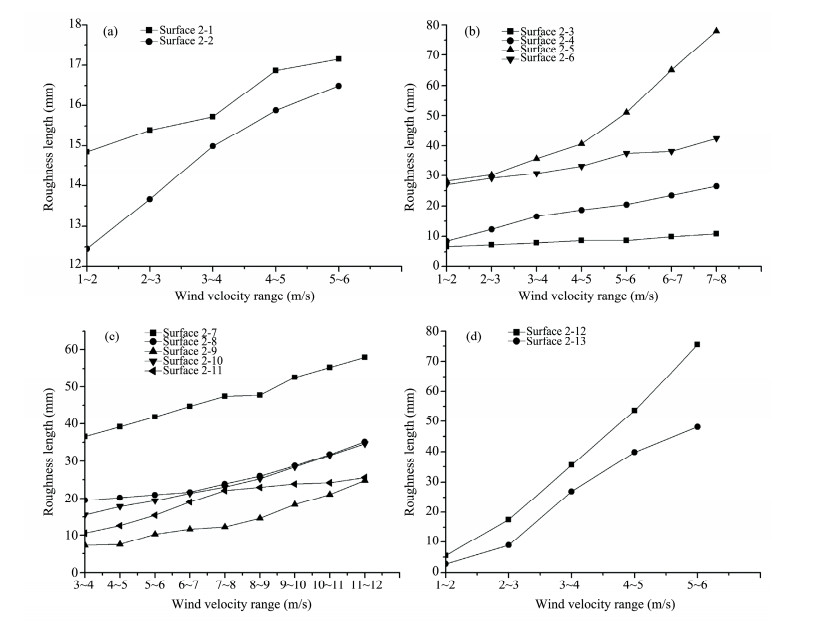
3.4 Roughness lengths of the vegetative surfacesThe roughness lengths for six types of herb surfaces and 13 types of shrub surfaces were calculated (Figures 4 and 5). These calculated results are different from previous research (Dong et al., 2001; Patil, 2006, Zhou et al., 2006; Zhang et al., 2012).

|
| Figure 4 Roughness lengths of herb surfaces. (a) surfaces covered by Achnatherum splendens; (b) surfaces covered by Agropyron cristatum; (c) surface covered by A. splendens and A. cristatum |
|
| Figure 5 Roughness lengths of shrub surfaces. (a) surfaces covered by Haloxylon ammodendron; (b) surfaces covered by Seriphidium terrae-albae; (c) surfaces covered by Artemisia ordosica; (d) surfaces covered by Salix integra and S. terrae-albae |
For herb surfaces, the roughness lengths do not always decrease with increasing wind velocity. Except on the surface of Ⅰ-1, roughness lengths increased with increasing wind velocity in given wind velocity ranges, and then decreased. For the different species, the turning points of increasing roughness length are different to each other. For example, on the surface of Ⅰ-2, covered by Achnatherum splendens, the turning point is on the wind velocity range of 3~4 m/s; but for the surfaces covered by Agropyron cristatum, the turning point appears on the wind velocity range of 9~10 m/s. For the surface covered by A. splendens and A. cristatum, the turning point of increasing roughness length is on the wind velocity range of 3~4 m/s, which is identical with that on the surface of Ⅰ-2 covered by A. splendens. However, passing the turning point, the decreasing rate of the roughness length is smaller than that on the surface of Ⅰ-2. On the surface of Ⅰ-1, the roughness length increases slowly with wind velocity.
For shrub surfaces, the roughness lengths are different with that of the herb surfaces, were roughness lengths increase with increasing wind velocity below the wind velocity of 12 m/s. The largest increasing rate of roughness length is on the surface of Ⅱ-12, covered by Salix integra and Seriphidium terrae-albae. In addition, checkerboard sand barriers with 1m×1m grids were also covered on this surface. Lacking checkerboard sand barriers, the increasing rate of roughness length of the surface of Ⅱ-13 is smaller than that on the surface of Ⅱ-12, but larger than the others. The minimum increasing rate of roughness length is on the surface of Ⅱ-3, which is covered by S. terrae-albae that has a smaller frontal area. Although having higher non-erodible elements, the roughness lengths of surfaces covered by Haloxylon ammodendron are not large enough. Besides, the surfaces covered by blending of different non-erodible elements, the shrub surfaces with larger vegetative frontal area would have larger roughness lengths, such as the surfaces of Ⅱ-5 and Ⅱ-7.
4 DiscussionAll the calculated roughness lengths of different non-erodible surfaces increased with increasing wind velocity in given wind velocity ranges. These results are different from previous work of Dong et al. (2001), Patil (2006), Zhou et al. (2006), and Zhang et al. (2012). In the following text, we discuss this phenomena and the caused reasons.
4.1 Zero-plane displacementThe influence of zero-plane displacement is usually considered for calculated roughness length. In this study, zero-plane displacements were ignored for sparse vegetation in windy seasons. It may not be a reliable measure on the effects of surface roughness under all conditions. In some field experiments, winds are suddenly displaced upward (displacement height) in a manner that may not be explained by roughness length alone (Brutsaert, 1982; Lee, 1990). In such cases, typically characterized by non-erodible roughness elements, the wind stress no longer reaches the surface.
Sometimes zero-plane displacement d can significantly affect the analysis of other micrometeorological parameters, especially the roughness length. The interpretation of zero-plane displacement and its physical significance becomes controversial (Molion and Moore, 1983). To date, there is no accurate method that can be applied to determine zero-plane displacement that in practice still remains a matter of rough estimation. Moreover, within the porous canopies typical of desert flora, Wolfe (1993) found that wind passed through all roughness elements and may contact the surface. In our observations, except that on the surface of Ⅰ-2, for the vegetation, the largest frontal area λis 0.301, and on the grave bed, the average coverage is only 0.35, so the wind can easily pass through the vegetation and reach the surface. Because the bare surface in the interspaces of non-erodible roughness elements still extracts momentum in an environment covered by sparse roughness elements, and the surface roughness length can increase to very large values before all wind stress is prevented from affecting the bare surface. Wind data collected by Lee (1990) in deserts with porous vegetation were re-evaluated by Wolfe (1993) to show that the data better fit a wind profile model without a zero-plane displacement height and with rather large roughness lengths (as much as 38 mm). Wolfe (1993) aerodynamically derived values of roughness length substantially exceed the largest values (6 mm) reported by Marticorena et al. (1997). Wolfe's result are consistent with the larger roughness length (as much as 71 mm) measured at some of the sites reported by MacKinnon et al. (1990).
In our observations, except that on the surface of Ⅰ-2, for the vegetation, with a small frontal area of 0.243 the roughness length is high (85.42 mm), and the wind velocity exceeds 5 m/s, so the wind stress can certainly reach the soil surface. For the grave bed and the surfaces covered by checkerboard sand barriers, there are enough interspaces between the non-erodible elements to make sure the wind stress can easily reach the surface. Hence, except the surface of Ⅰ-2, for all the non-erodible surfaces we observed, there is no need to consider the zero-plane displacement when the wind profile parameters were calculated.
For the surface of Ⅰ-2, the coverage is high (1.0), the frontal area is 1.049, and the height is 0.912 m. Thus, wind stress barely reaches the soil surface, and the zero-plane displacement must be considered. But as an individual case, Ⅰ-2 only expressed a trend of roughness length changing with wind velocity, and thus does not affect the whole research work.
4.2 Variation of roughness lengthsThe checkerboard sand barriers we observed are made of wheat straw and cotton stem, respectively. Although the wheat straw has some flexibility, much of the wheat straw is buried underground, and barrier density is very thick. Sand barriers do not change their shapes even in strong wind environments. Thus, relative to vegetation with flexible characters, gravel and checkerboard sand barriers are recognized as rigid non-erodible elements.
4.2.1 Roughness lengths of surfaces covered by rigid roughness elementsOn surfaces covered by rigid non-erodible elements, all roughness lengths increase with wind velocity (Figures 2 and 3). For invariable shapes of non-erodible elements, increasing roughness lengths were caused by the emission of dust or sand, which would increase surface resistance and prevent wind stress from reaching the soil surface. The dust emission was difficult to observe, however, when wind velocity exceeded 6 m/s, the saltation sand was captured by sand traps. Therefore, when the wind velocity exceeds 6 m/s, the increasing rates of roughness length would increase significantly.
On the surfaces covered by checkerboard sand barriers, the roughness length of surfaces with denser grids were larger than that on the surface with sparser grids in every wind velocity range. This is due to airflow blowing over the surface with denser grids generating more violent turbulence than what is generated on the surface with sparser grids. Near surface turbulence increases surface resistant and prevents wind stress from reaching the surface. Moreover, the checkerboard sand barriers made of cotton stem has larger gaps than that made of wheat straw. Grant and Nickling (1998) demonstrated that the resistance of porous elements is greater than solid elements with the same physical dimensions, because porous elements would absorb more momentum than solid elements. The greater resistance could cause larger roughness length based on wind profile equations. Therefore, roughness length generated by the surface covered by cotton stem checkerboard sand barriers is larger than the surface covered by wheat straw barriers.
4.2.2 Roughness lengths of vegetative surfacesMost previous work demonstrated that the roughness length of the vegetative surface would decrease with wind velocity (Dong et al., 2001; Patil, 2006; Zhou et al., 2006; Zhang et al., 2012), due to the natural flexible character of vegetation. However, light breeze cannot significantly reduce vegetation height, especially for trees and shrubs. The roughness length increase with wind velocity can be explained through absorbing the momentum of wind stress, with vegetation close to each other and shrinking interspaces between the vegetation. This would increase surface resistance and prevent wind stress from reaching the surface.
However, on some herb surfaces, roughness lengths decreased with wind velocity when the wind velocity reached a given value. This phenomenon can be explained by the previous theories of Dong et al. (2001), Patil (2006), Zhou et al. (2006), and Zhang et al. (2012). The wind stress bends the vegetation's stems and reduces vegetation height due to the flexible nature of vegetation.
From Figure 4, it can be speculated that stems of Achnatherum splendens are softer than Agropyron cristatum. Because the roughness length of the surface covered by A. splendens would decrease with the wind velocity when the velocity exceeds 3 m/s, on the surfaces covered by A. cristatum, the wind velocity would need to exceed 9 m/s. For the surface covered by A. splendens and A. cristatum, when wind velocity exceeds 3 m/s, A. splendens height is reduced, and A. cristatum height remains unchanged. Hence, the roughness length of this surface decreases with wind velocity when wind velocity exceeds 3 m/s, and the decrease rate is less than that on the surface covered by A. splendens.
The stems of shrub's are harder than herbs, and in the observed wind velocity ranges, wind stress cannot reduce their heights, but shrinks the interspace of the vegetation. Consequently, the roughness lengths of shrub surfaces increase with wind velocity in given wind velocity ranges.
4.3 Influence of vegetative parameters for roughness lengthIn this study, several vegetation parameters were measured to find which one could significantly affect the roughness length. So, correlation analysis among the vegetation parameters and roughness length were made. The roughness lengths in common wind velocity ranges (3~4 m/s, 4~5 m/s, and 5~6 m/s) were selected, and the results are presented in Table 4.
| Surface types | Vegetation parameters | Roughness length in different wind velocity ranges (mm) | ||
| 3~4 m/s | 4~5 m/s | 5~6 m/s | ||
| Herb surface | Height | 0.660 | 0.663 | 0.666 |
| Separation | -0.283 | -0.281 | -0.277 | |
| Width | 0.776 | 0.777 | 0.779 | |
| Coverage | 0.995 | 0.996 | 0.996 | |
| Frontal area | 0.990 | 0.991 | 0.991 | |
| Shrub surface | Height | 0.143 | 0.196 | 0.190 |
| Separation | -0.265 | -0.238 | -0.210 | |
| Width | 0.218 | 0.260 | 0.208 | |
| Coverage | 0.507 | 0.324 | 0.147 | |
| Frontal area | 0.564 | 0.390 | 0.237 | |
From Table 4, the roughness length affected by these vegetation parameters by different degrees were obtained. For the different sample size of both surfaces types, the correlation coefficients between the vegetation parameters and roughness length of the herb surfaces are all larger than that of shrub surfaces. The vegetation's coverage and frontal area could affect the roughness length more significantly than the other parameters either on herb or shrub surfaces. This result is different with what observed in wind tunnels (Dong et al., 2001). This might explain why the roughness element we measured is not dense enough. Airflow around a single roughness element is separated into six energy regions: the covered area, slight wind area immediately behind the plant, the wake zone, the zone of accelerated flows on both sides, and the unaffected area (Wasson and Nanninga, 1988). When vegetation is sparsely distributed, the flow regime is one of isolated flow, where all six regions can be fully developed. However, as the density increases the energy regions around the plants tend to interfere with each other, resulting in wake flow and eventually skimming flow if the density is sufficient (Lee, 1991). In the wake flow some parts of the downwind plants are in the wake area of the upwind ones. In skimming flow the downwind plants are almost totally immersed in the wake of the upwind ones. Also, wind stress or the resistance of a single plant is reduced by adding plants at a given velocity, resulting in progressive stable stress. However, the frontal areas of vegetation we measured are all smaller than 0.31, except that of the surface of Ⅰ-2. In sparse vegetative surfaces, increasing vegetation density would generate more slight wind areas, and fewer zones of accelerated flow, which would increase surface resistance and preventing wind stress from reaching the surface. Therefore, the coverage and frontal area of vegetation would significantly affect roughness length.
4.4 Protective results of different non-erodible surfacesThe arrays of checkerboard sand barriers are different from gravel and vegetation, and the protective result of these surfaces was evaluated firstly. Figure 3 shows that the roughness length of the surface covered by cotton stems barriers are all larger than the surface covered by wheat straw barriers. Thus, the former barriers can reduce wind velocity more efficiently than the latter. Through observation results in Shapotou, China, Qu et al. (2007) demonstrated that wheat checkerboard sand barriers with 0.5m×0.5m grids are easily buried, and then lose the protective result. However, the checkerboard sand barriers made of cotton stems have larger pores than that of wheat straw, and the sand is not easily deposit on the upwind sections of the barriers. The checkerboard sand barriers made of cotton stems were built in 2010, and to date, the sand barriers have not be buried; and in the grids, the concave surfaces are still intact. Therefore, ignoring the costing, the cotton stem checkerboard sand barriers with 0.5m×0.5m grids provide a more efficient protective result than that made of wheat straw with 1m×1m grids.
To evaluate the protective results of gravel and vegetation, a common parameter of coverage should be selected. The aforementioned figures show that the roughness length of gravel beds are all smaller than that of vegetative surfaces in similar wind velocity ranges, although the coverage of gravel is larger than most vegetation coverage. There are three reasons that cause this phenomenon, firstly, gravel heights are smaller than that of vegetation; secondly, gravel lack pores as opposed to vegetation; thirdly, vegetation has flexible characters. The fact that height of roughness element could affect roughness length was discussed in detailed by previous scholars (Dong et al., 2001; Zhou et al., 2006; Zhang et al., 2012), and thus is not included in this paper. The higher roughness lengthvalues of vegetative surfaces compared to that of gravel bed result from the greater momentum extracting potential of these porous and flexible roughness elements. Flexibility in the stems and branches of the vegetation allows energy to dissipate through the bending and swaying movement, and property results in the change of form and resistance properties of vegetation with increasing wind speeds as a result of change of their alignment, branch position, and overall streamlining of their form. Therefore, vegetation could provide a more effective protective result than gravel.
In these different types of vegetation, the blending of different non-erodible elements, especially the combination of blending of vegetation and checkerboard sand barriers could provide more effective protective results, because these surfaces could provide larger roughness lengths, and faster increasing rates of both parameters than other surfaces having similar vegetation coverage, plant height, or frontal area of vegetation, such as the surfaces of Ⅰ-6, Ⅱ-12, and Ⅱ-13. Different vegetation usually has different heights, flexibility, alignment, branch position, or form. When the airflow blows over the surface covered by blending of different non-erodible elements, the height, alignment, branch position and form of the different vegetation would change in different degrees, which result in vegetation having greater momentum extraction potential, and increasing the roughness length of the surface.
5 ConclusionsThe roughness lengths of different non-erodible surfaces as influenced by wind velocity, and characters of non-erodible roughness element were measured in the field. The conclusions are drawn as follows:
Roughness length increases with increasing wind velocity in a given wind velocity range either on the surfaces covered by rigid roughness elements or covered by vegetation. On surfaces covered by rigid roughness elements, the roughness increases abruptly when saltation emission occurs; while, on the vegetative surfaces, wind stress could compress the interspaces between the vegetation, which would increase surface resistance and preventing wind stress from reaching the surface.
Our observations reveal that light breeze cannot bend the vegetation's stem and reduce the vegetation's height, significantly. Different vegetation have different flexibility, thus the threshold wind velocity for bending the vegetation is also different. For Achnatherum splendens, wind velocity needs to exceed 4 m/s, and for Agropyron cristatum, it needs to exceed 10 m/s. However, for Artemisia ordosica, there is no obvious vegetation bending even through the wind velocity reached 12 m/s.
The roughness length of the vegetative surfaces was affected by the combined action of vegetation height, separation, width, coverage and frontal area. Correlation analysis revealed that vegetation coverage and frontal area affect the roughness length more significantly than the other parameters either on the herb or shrub surfaces.
The protective results of these non-erodible elements were evaluated. The checkerboard sand barriers made of cotton stem could provide more effective protection than that made of wheat straw, for the former have more pores than the latter. In similar coverage conditions, vegetation could protect the surface from wind erosion more than gravel, because the vegetation has characters of flexibility and porosity, which have greater momentum extracting potential. For vegetative surfaces, the blending of different non-erodible elements especially the combination of blending of vegetation and checkerboard sand barriers could provide more effective protection to the surface, because the height, alignment, branch position and form of the different vegetation would change in different degrees affected by wind stress.
Acknowledgments:This work was financial supported by the Nature Science Foundation of China (Grant Nos. 41601009, 41401645), and the Open Fund of Yellow River sediment key laboratory of Ministry of Water Resources of China (Grant No. 2015004).
| Abtew W, Gregory JM, Borreli J, 1989. Wind profile:estimation of displacement height and aerodynamic roughness. Transactions of the ASAE, 32: 521–527. DOI: 10.13031/2013.31034 |
| Brutsaert W, 1982. Evaporation into the Atmosphere:Theory, History, and Applications. Boston:D. Reidel Publishing, pp. 299. |
| Dickerson RR, Kondragunta S, Stenchikov G, et al, 1997. The impact of aerosols on solar ultraviolet radiation and photo-chemical smog. Science, 278: 827–830. DOI: 10.1126/science.278.5339.827 |
| Dong ZB, Gao SY, Fryear DW, 2001. Drag coefficients, roughness length and zero-plane displacement height as disturbed by artificial standing vegetation. Journal of Arid Environments, 49: 485–505. DOI: 10.1006/jare.2001.0807 |
| Du HQ, Xue X, Wang T, 2014. Estimation of saltation emission in the Kubuqi Desert, North China. Science of the Total Environment, 479-480: 77–92. DOI: 10.1016/j.scitotenv.2014.01.095 |
| Grant PF, Nickling WG, 1998. Direct field measurement of wind drag on vegetation for application to windbreak design and modeling. Land Degradation Development, 9: 57–66. DOI: 10.1002/(ISSN)1099-145X |
| Hoffmann C, Funk R, Wieland R, et al, 2008. Effects of grazing and topography on dust flux and deposition in the Xilingele grassland, Inner Mongolia. Journal of Arid Environments, 72: 792–807. DOI: 10.1016/j.jaridenv.2007.09.004 |
| Lee JA, 1990. The effect of desert shrubs on shear stress from the wind:an exploratory study. Unpublished Ph.D. Thesis. De-partment of Geography, Arizona State University, pp. 181. |
| Lee JA, 1991. The role of desert shrub size and spacing on wind profile parameters. Physical Geography, 12: 72–89. |
| Lettau H, 1969. Note on aerodynamic roughness-parameter esti-mation on the basis of roughness-element description. Journal of Application Meteorology, 8: 828–832. DOI: 10.1175/1520-0450(1969)008<0828:NOARPE>2.0.CO;2 |
| Liu X, Dong Z, 2002. Estimating of displacement height using Marquardt Method. Journal of Desert Research, 22: 233–236. |
| MacKinnon DJ, Elder DF, Helm PJ, et al, 1990. A method of evaluating effects of antecedent precipitation on dust storms and its application to Yuma, Arizona. 1981-1988. Climate Change, 17: 331–360. DOI: 10.1007/BF00138374 |
| Marticorena B, Bergametti G, Aumont B, et al, 1997. Modeling the atmospheric dust cycle:2. Simulation of Saharan dust sources. Journal of Geophysical Research, 102: 4387–4404. DOI: 10.1029/96JD02964 |
| Molion LCB, Moore CJ, 1983. Estimating the zero-plane dis-placement for tall vegetation using a mass conservation method. Boundary-Layer Meteorology, 26: 115–125. DOI: 10.1007/BF00121537 |
| Monteith JL, 1973. Principles of Environmental Physics. London:Edward Arnold, pp. 1-418. |
| Patil MN, 2006. Aerodynamic drag coefficient and roughness length for three seasons over a tropical western Indian station. Atmospheric Research, 80: 280–293. DOI: 10.1016/j.atmosres.2005.10.005 |
| Qiu GY, Lee IB, Shimizu H, et al, 2004. Principles of sand dune fixation with straw checkboard technology and its effects on the environment. Journal of Arid Environments, 56: 449–464. DOI: 10.1016/S0140-1963(03)00066-1 |
| Qu JJ, Zu RP, Zhang KC, et al, 2007. Field observations on the protective effect of semi-buried checkerboard sand barriers. Geomorphology, 88: 193–200. DOI: 10.1016/j.geomorph.2006.11.006 |
| Raupach MR, 1992. Drag and drag partition on rough surfaces. Boundary-Layer Meteorology, 60: 375–395. DOI: 10.1007/BF00155203 |
| Riksen M, Brouwer F, Graaff J, 2003. Soil conservation policy measures to control wind erosion in northwestern Europe. Catena, 52: 309–326. DOI: 10.1016/S0341-8162(03)00020-1 |
| Sellers PJ, Mintz Y, Sud YC, et al, 1986. A simple biosphere model (SIB) for use within general circulation models. Journal of Atmosphere Sciences, 43: 505–531. DOI: 10.1175/1520-0469(1986)043<0505:ASBMFU>2.0.CO;2 |
| Shao YP, 2001. A model for mineral dust emission. Journal of Geophysical Research, 106(20): 239–254. DOI: 10.1029/2001JD900171 |
| Skidmore EL, 2000. Air, soil, and water quality as influenced by wind erosion and strategies for mitigation. In:AGRONENVIRON2000, Second International Symposium of New Technologies for Environmental Monitoring and Agro-Applications Proceedings. Tekirdag, Turkey, pp. 216-221. |
| Wasson RJ, Nanninga PM, 1986. Estimating wind transport of sand on vegetated surfaces. Earth Surface Processes and Landforms, 11: 505–514. DOI: 10.1002/esp.3290110505 |
| Wolfe SA, 1993. Sparse vegetation as a surface control on wind erosion. PhD Dissertation, University of Guelph, pp. 257. |
| Wolfe SA, Nickling WG, 1996. Shear stress partitioning in sparsely vegetated desert canopies. Earth Surfaces and Processes Landforms, 21: 607–619. DOI: 10.1002/(SICI)1096-9837(199607)21:<607::AID-ESP660>3.0.CO;2-1 |
| Zhang Q, Zeng J, Yao T, 2012. Interaction of aerodynamic rough-ness length and windflow conditions and its parameterization over vegetation surface. Chinese Science Bulletin, 57: 1559–1567. DOI: 10.1007/s11434-012-5000-y |
| Zhou YL, Sun XM, Zhu ZL, et al, 2006. Surface roughness length dynamic over several different surfaces and its effects on modeling fluxes. Sciences of China (Series D-Earth Sciences), 49: 262–272. DOI: 10.1007/s11430-006-8262-x |
 2017, 9
2017, 9


