Article Information
- JinKui Wu, ShiWei Liu, LePing Ma, Jia Qin, JiaXin Zhou, Hong Wei . 2016.
- Comparison analysis of sampling methods to estimate regional precipitation based on the Kriging interpolation methods: A case of northwestern China
- Sciences in Cold and Arid Regions, 8(6): 485-494
- http://dx.doi.org/10.3724/SP.J.1226.2016.00485
Article History
- Received: March 18, 2016
- Accepted: July 21, 2016
2. State Key Laboratory of Cryospheric Sciences, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou, Gansu 730000, China;
3. Shule River Basin Water Resources Administration Bureau of Gansu Province, Yumen, Gansu 735200, China
Precipitation is one of the most essential variables of meteorology and hydrology(Rui,2004). It is also the one essentially required for a number of applications such as natural resource management,agriculture management,irrigation scheduling,ecosystem modeling,and hydrological modeling(Ashiq et al.,2010). Precipitation data are usually available at certain locations where weather stations are set up. For the majority of locations,such as mountainous,marine and oceanic regions,it is difficult and expensive to acquire continuous spatial data(Wang et al.,2014). Interpolation is a spatial analysis method that constructs new data points within the range of a discrete set of known data points. In meteorology and hydrology,by using geographical(e.g.,weather stations)and temporal data from observation points,interpolation is used to predict climate variables in areas where there are no weather observation data available(Alvarez et al.,2014). The precision of spatial interpolation of precipitation is related to the actual spatial variability of the precipitation,the distribution of the stations,and the interpolation methods used(Kong and Tong,2008). The spatial variability of precipitation is determined by natural properties,which are not controllable. Therefore,to estimate precipitation accurately,it is necessary to have rain gauges distributed in optimal locations and to apply appropriate interpolation techniques for estimating important parameters(Yavuz and Erdoğan,2012).
Many spatial interpolation methods have been developed to estimate the values of environmental variables at unmeasured locations for creating a continuous surface from sampled point values,and over the last decade they have been increasingly used in a wide range of studies,including ecology,hydrology,fire modeling,and water resources(Bostan et al.,2012; Alvarez et al.,2014). The interpolation methods can be divided into two kinds: deterministic and geostatistical interpolation techniques. Deterministic interpolations use mathematical functions to generate gridded data from the measured points based on either the extent of similarity or the degree of smoothing(Johnston et al.,2001; Ashiq et al.,2010). Among various deterministic interpolation techniques,inverse distance weighted,local polynomial interpolation,and radial basis functions are used to generate models. Geostatistic interpolations are based on the theory of regionalized variables and rely on both statistical and mathematical functions. A variogram model is used to describe the spatial continuity of the input data to estimate values at unsampled locations. From this group,ordinary Kriging and its multivariate extension,ordinary co-Kriging,are used to generate models(Ashiq et al.,2010).
Regarding precipitation,much of the effort has been focused on identifying appropriate interpolation methods. Lloyd(2005)studied the effect of elevation on estimation of monthly precipitation in Great Britain by comparing moving window regression,inverse distance weight(IDW),ordinary Kriging(OK),simple Kriging with a locally varying mean,and Kriging with external drift(KED),and concluded that KED provided the most accurate estimates of precipitation when judged by cross-validation estimation error summary statistics. Chen et al.(2010)focused on identifying an accurate method to produce gridded daily precipitation in China based on the observed data at 753 stations for the period 1951–2005. They used and compared five interpolation methods,including ordinary nearest neighbor,local polynomial,radial basis function,inverse distance weighting,and ordinary Kriging. Cross-validation showed that the ordinary Kriging based on seasonal semi-variograms gave the best performance. Wei et al.(2005)compared interpolation approaches,statistical models,and comprehensive approaches,including nine methods to estimate precipitation resources for rainwater harvesting for agriculture in semi-arid lands in China. Their results indicated that the simulating precision of the comprehensive method was the best of the nine approaches,while among the seven interpolation approaches,the precision of the ordinary Kriging method was the best.
These researches indicated that there is no absolutely best interpolation method; the best method can be chosen by taking the actual situation of the study area into account. Among the various interpolation methods,no method is always optimal; the best interpolation method for a specific situation can only be obtained by comparing their results(Sun et al.,2009). In studies of precipitation interpolation in northwestern China,ordinary Kriging and co-Kriging performed better(Fang et al.,2005; Chu et al.,2008; He et al.,2008). In this paper,we used the OK method to estimate the regional surface precipitation in northwestern China.
The distribution of meteorological stations also impacts the precision of precipitation interpolation(Yavuz and Erdoğan,2012). Numerous studies have shown that the accuracy of the interpolation methods is comparatively more reliable in areas of greater observation site density(Chen et al.,2010). The distribution of precipitation stations is subject to natural factors and socio-economic conditions,and if the representativeness of some stations is relatively poor,it will limit the accuracy of the precipitation interpolation.
Currently,the sampling model method can aggregate weather stations to optimize the number and location of the stations,and the resulting samples will have a higher accuracy of interpolation and greater representativeness than others in regional precipitation estimation. Therefore,this method renders the interpolation results of regional precipitation more accurate. The sampling model mainly includes simple random sampling,systematic sampling,cluster sampling,spatial random sampling,spatial stratified sampling,and spatial sandwich sampling,and has been widely used in fields such as sociology,natural sciences,economics,and population studies(Cao et al.,2008; Jiang et al.,2008). The sandwich sampling method will stratify the sample layer according to prior knowledge,which can improve the accuracy of statistical results. For example,Wang et al.(2002,2013)used the spatial sandwich method to estimate the proportion of cultivated land in Shandong Province,China in 2000,and they suggested certain situations where sandwich estimation might be expected to do better than block Kriging estimation and hierarchical Bayesian estimation. The sandwich sampling method is well applied in soil evaluation and forest area estimation. For example,Chen et al.(2012)investigated the soil Cr content in Zengcheng City,Guangdong Province of China,with three different methods for sampling analysis: spatial random sampling,spatial stratified sampling,and spatial sandwich sampling. They found that the regional distribution result error of ordinary Kriging interpolation by sample points which were obtained by the sandwich sampling method was the minimum of the three methods. Zhang J and Zhang Y(2011)used different sampling methods to estimate forest areas,and their results showed that the accuracy of the sandwich model of spatial sampling was the highest,followed by the spatial stratified sampling and the spatial random sampling methods.
Northwest China(31°35'N–49°15'N,73°25'E– 110°55'E)is located in the central part of the Eurasian continent,and includes Xinjiang,Qinghai,Gansu,Ningxia,and Shaanxi provinces(Liu et al.,2013). The total area is approximately 3.04 million km2,accounting for more than 30% of China's total terrestrial area. The Kunlun Mountains and the northeastern Qinghai-Tibet Plateau are the southern boundary of the area,and they block the vapor from the Indian Ocean. The Altai Mountains are the northern boundary,blocking the vapor from the Arctic Ocean. The Tianshan Mountains lie in the middle of Xinjiang and form landscapes of alpine meadows,inland basins,gobi deserts,and widespread sandy deserts. This region is controlled by a continental climate and the average annual precipitation is only 130 mm,with an increasing trend during 1956–2010(Shi et al.,2002; Shen et al.,2013). The Loess Plateau is the eastern boundary,which blocks the vapor from the Pacific Ocean. This region is controlled by a monsoon climate,and the average annual precipitation is about 500 mm with a negative changing trend(−29.11 mm/(50a))(Wang et al.,2012). The Hexi Corridor is the middle area,connecting the Tianshan Mountains and the Loess Plateau,whose annual precipitation is about 200 mm with an increasing trend(3.95 mm/(10a))(Meng et al.,2012). However,the annual precipitation is still relatively sparse in southern Xinjiang and the Hexi Corridor,while relatively abundant in northern Xinjiang and the Loess Plateau.
Analyzing the differences of precipitation in an entire region and evaluating whether the existing meteorological stations adequately reflect the regional precipitation can help to grasp the actual regional precipitation and plan industry development according to industrial water consumption,and optimize the use of precipitation resources in various regions. In addition,the spatial interpolation of precipitation can also provide basic data for the simulation of area runoff,and prediction and management of droughts,floods,and other hydrological problems.
In this study,three sampling methods were used to sample the meteorological stations in northwestern China: spatial random sampling,spatial stratified sampling,and spatial sandwich sampling. The samples were interpolated with the ordinary Kriging method to estimate the regional precipitation,and the accuracy of the different samples were compared to attempt to select a group of stations that are more representative in the study area.
2 Materials and methods 2.1 Spatial autocorrelation analysisSpatial autocorrelation refers to the relevance of the same property or phenomenon in different spatial locations,that is,the spatial heterogeneity of the same property or phenomenon(Zhang S and Zhang K,2007). Moran's I coefficient method is a commonly utilized index to measure spatial autocorrelation(Moran,1948,Moran,1950):
| $I=\frac{n}{{{S}_{0}}}\frac{\sum{_{i=1}^{n}}\sum{_{j=1}^{n}}{{w}_{i,j}}{{z}_{i}}{{z}_{j}}}{\sum{_{i=1}^{n}}z_{i}^{2}}$ | (1) |
where zi is the deviation of the attribute of element i and its average; wi,j is the spatial weight of elements i and j; n and S0 are the total number of elements and aggr egation of all spatial weights,respectively. S0 is:
| ${{S}_{0}}=\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{w}_{i,j}}}}$ | (2) |
The value of Moran's I is typically between −1 and 1. If I is a positive number,it indicates spatial elements for clustering distribution,and for discrete distribution if I is a negative number. A larger value of I indicates greater correlation of spatial distribution,and means spatial elements are more gathered in space and more approximate in attribute value.
2.2 Sampling methods 2.2.1 Spatial random sampling method Unlike simple random sampling,the spatial random sampling method takes the spatial autocorrelation into account; the variance of the mean value estimation needs to be adjusted according to the degree of correlation in the spatial sampling objects(Wang et al.,2009). The mean and variance are:| $\bar{y}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{y}_{i}}}$ | (3) |
| $v\left( n \right)=E\left[ \frac{1}{n}\sum\limits_{i}^{n}{{{y}_{i}}}-\frac{1}{A}\int\limits_{A}{y\left( s \right)\text{d}s} \right]=\frac{\sigma _{p}^{2}}{n}-\frac{E\left[ C\left( X,Y \right) \right]}{n}$ | (4) |
| $\overline{{{y}_{z}}}=\frac{1}{{{n}_{z}}}\sum\limits_{i=1}^{{{n}_{z}}}{{{y}_{zi}}}$ | (5) |
| $v\left( \overline{{{y}_{z}}} \right)=E{{\left( \overline{{{y}_{z}}}-\overline{{{Y}_{z}}} \right)}^{2}}$ | (6) |
| $\bar{y}=\frac{1}{n}\sum\limits_{z=1}^{L}{{{n}_{z}}}\overline{{{y}_{z}}}$ | (7) |
| $v\left( \overline{y} \right)=\sum\limits_{z=1}^{L}{W_{z}^{2}}\left( \overline{{{y}_{z}}} \right)$ | (8) |
| $\overline{{{y}_{r}}}=\sum\limits_{z=1}^{{{N}_{rz}}}{{{W}_{rz}}}\overline{{{y}_{z}}}$ | (9) |
| $v\left( \overline{{{y}_{r}}} \right)=\sum\limits_{z=1}^{{{N}_{rz}}}{W_{rz}^{2}}\left( \overline{{{y}_{z}}} \right)$ | (10) |
| ${{W}_{rz}}={{N}_{rz}}/{{N}_{r}}$ | (11) |
In contrast with deterministic methods,Kriging is a powerful statistical interpolation method which has the capability of giving unbiased predictions with minimum variance and taking account of spatial correlations and statistical relationships between measured points(Krige,1966). The OK estimate is a linear weighted average of the available non-observations defi ned in Equation(12)as:
| $Z\left( s \right)=\sum\limits_{i=1}^{n}{{{\lambda }_{i}}z\left( {{s}_{i}} \right)}$ | (12) |
where Z(s)is the OK estimate at location s,λi is the OK weight,and si are the observation locations.
The weight of different locations is based on their spatial relationship. Kriging uses the semi-variogram as a measure of dissimilarity between observations. The semi-variogram is a function of both distance and direction,so it can account for direction-dependent variability(Yavuz and Erdoğan,2012).
However,Kriging methods not only provide predictions,but also quantify the prediction error. In this study,the performance comparison of different samples was made using a cross-validation procedure.
The root mean squared error(RMSE)is an accuracy performance measure that is frequently used as a measure of magnitude of errors(Equation(13))(Lloyd,2005):
| $RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left( Z\left( s \right)-z\left( {{s}_{i}} \right) \right)}^{2}}}}$ | (13) |
where Z(s)is the predicted value; z(si)is the observed value at the sampling point si; and n is the number of sample points.
The root mean square standardized error(RMSSE)is a measure of the goodness of the assessment of the prediction error. If the prediction error variance is correctly assessed,then the ratio should on average be close to 1(Equation(14))(Bostan et al.,2012):
| $RMSSE=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\frac{\left( Z\left( s \right)-z\left( {{s}_{i}} \right) \right)}{\sigma _{PE}^{2}\left( {{s}_{i}} \right)}}^{2}}}$ | (14) |
where $\sigma _{PE}^{2}$ is the prediction error variance at location si.
2.4 Data sourceThe precipitation data were downloaded from the China Meteorological Data Sharing Service System. The average annual precipitation data of 155 meteorological stations in Northwest China were used for sample analysis and comparison. The distribution of these sites is shown in Figure 1.
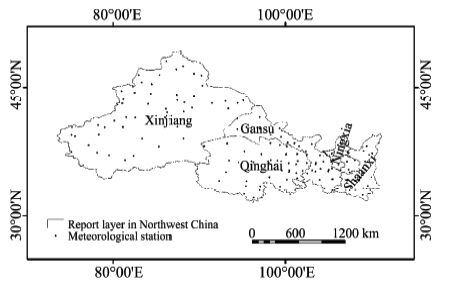
|
| Figure 1 The distribution of meteorological stations and partition of report layer |
Space stratification takes samples of the small variances in the inner layer and large variances among the different layers,and makes the spatial elements have relatively approximate attribute values in the same layer. According to Tobler's first law of geography(Tobler,1970,2004),the closer distance of objects,the higher their degree of similarity,so the objects in space are continuous wholes. Thus,precipitation in the study area was comprehended as being larger in the southeast and smaller in the Northwest,and the southern Xinjiang and northern Gansu provinces were found to be the most arid regions in the area. We divided the whole Northwest China area into five parts based on prior knowledge from local people to guarantee that the precipitation differences were small inside each layer and large among the other layers,and all of the layers were spatially continuous. This stratification was called the knowledge layer(Wang et al.,2002). The first strata included the southern region of Shaanxi Province and a small region in the southwest part of Qinghai Province; the second strata included the middle area of Shaanxi,the southern region of Gansu,and the southwestern region of Qinghai; the third strata included the northern region of Shaanxi,the southern region of Ningxia,the middle areas of both Gansu and Qinghai,and a small part of the northeast region of Xinjiang; the fourth strata included northern Ningxia,the middle Gansu and Qinghai,and the northern Xinjiang; and the fifth strata included the northern regions of both Gansu and Qinghai.
Sandwich sampling joins the report layer and solves the sampling problem of multiple report units. It can divide the whole layer into report layers according to the user's needs,and deduce the average and variance of every report unit. The administrative layer was carried as the report layer in this paper,shown in Figure 1. The knowledge layer is shown in Figure 2.
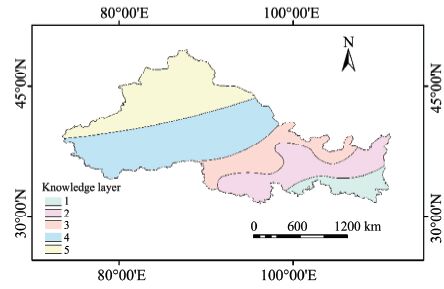
|
| Figure 2 The partition of the knowledge layer |
In this paper,Moran's I coefficient method was used to measure the spatial autocorrelation level of regional precipitation by ArcGIS 10.2. The result showed the I index as approximately 0.75,P<0.01,and the Z score was approximately 17.2. It indicated that there was an observable positive autocorrelation of precipitation in the study area at the 99% confidence level,and showed the state of aggregation in the space.
Each station had a higher regional representation if the high and low values of precipitation were aggregated in space rather than having a random distribution. Sampling of the original stations could thus determine which station was highly representative of the region.
3.2 Sampling resultsIn this paper,the pure random sampling method proposed by Cochran was used to determine the sample c apacity. The formula is:
| $n=\frac{\left( t\cdot {{S}_{\text{td}}} \right)}{{{d}^{2}}}$ | (15) |
where n is the capacity of sample; t is the standard normal deviation according to significance level α; Std is the standard deviation of the samples; and d is the product of the sample mean and the relative error.
The Std was 217.7 and the sample mean was 305.5. The t values were 1.6449,1.9600,and 2.5758 at the confidence levels of 90%,95%,and 99%,respectively. According to actual conditions,the relative error and the confidence level were set at 60% and 99%,respectively. Eighty-five sample points were chosen to compare the spatial sampling.
The software sampling package was used to sample the 155 stations by spatial random sampling,spatial stratified sampling,and spatial sandwich sampling. The confidence interval,spatial autocorrelation coefficient,population variance,and absolute error of the spatial random sample were set 0.05,0.4,217.7,and 16,respectively. The confidence interval of the spatial stratified sampling was set 0.05 and the variances of each layer were,respectively,138,102,95,20,and 109. The parameters of the sandwich sampling were the same as the stratified sampling,but with added report hierarchical information. The sampling results are shown in Table 1.
| Knowledge layer | All stations | Spatial random sampling | Spatial stratified sampling | Spatial sandwich sampling | |||||||
| Amount | Percentage | Amount | Percentage | Amount | Percentage | Amount | Percentage | ||||
| 1 | 21 | 0.1355 | 10 | 0.1176 | 16 | 0.1882 | 16 | 0.1882 | |||
| 2 | 47 | 0.3003 | 27 | 0.3176 | 27 | 0.3176 | 27 | 0.3176 | |||
| 3 | 28 | 0.1806 | 15 | 0.1765 | 15 | 0.1765 | 15 | 0.1765 | |||
| 4 | 20 | 0.129 | 12 | 0.1412 | 3 | 0.0353 | 3 | 0.0353 | |||
| 5 | 39 | 0.2516 | 21 | 0.2471 | 24 | 0.2824 | 24 | 0.2824 | |||
Ordinary Kriging was utilized to interpolate the regional value of annual precipitation with all of the stations and sampling results. The interpolation results are shown in Figures 3a-d.
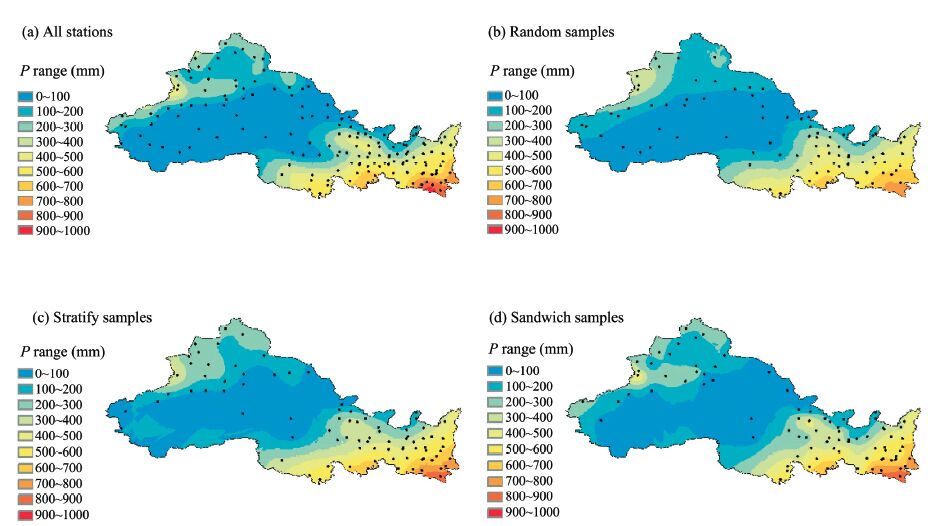
|
| Figure 3 The ordinary Kriging interpolation of precipitation under different distributions of the sampling methods |
According to these results,the interpolation by spatial sandwich samples had the best result compared to the spatial random and spatial stratified samples. All three of the sampling types estimated that there was more precipitation in the southeast,less in the northwest,and least in the middle area. The interpolation result of the spatial random samples was gradually and thinly distributed,but could not reflect the extreme values of the whole area,such as northwestern Xinjiang,southern Shaanxi,and central Gansu. The interpolation of the spatial stratified samples gave better estimates in southern Shaanxi,whereas the spatial random samples gave worse estimates. However,only the spatial sandwich samples estimated the extreme values in northwestern Xinjiang and central Gansu.
3.4 Report informationThe three kinds of sampling methods could all report the precipitation information of the study area. The spatial random sampling method could only report the mean value and the standard deviation of precipitation of the samples in whole area. The spatial stratified sampling method could report more information,such as the mean value of each knowledge layer. And the spatial sandwich sampling method could not only report the information of the knowledge layers,but also of the report layers. In the analysis of regional annual precipitation with spatial sandwich sampling,we could obtain the information of different report layers,such as watershed layers,raster layers,and administration layers. The mean interpolated values of Xinjiang,Qinghai,Gansu,Ningxia and Shaanxi were 118.07,394.98,291.59,336.46,and 526.72,respectively,compared with observed values of 143.39,368.45,297.49,251.75,and 612.23. The mean value of Ningxia had the largest deviation because only 4 samples from 10 stations in Ningxia were selected in the spatial sandwich sampling.
3.5 Error analysisWe used cross-validation of the annual precipitation interpolation of all 155 stations and the three sampling methods to produce an error analysis and evaluate the accuracy of the samples. The results are shown in Table 2.
| Sampling methods | ME | MSE | RMSSE | RMSE | ASE | |RMSE−ASE| |
| All stations | 0.0323 | 0.0027 | 1.0062 | 76.46 | 85.3 | 8.84 |
| Spatial random sampling | −2.0870 | −0.0165 | 0.8714 | 94.64 | 111.78 | 17.14 |
| Spatialst ratified sampling | −0.3505 | −0.0050 | 1.1035 | 105.81 | 98.15 | 7.66 |
| Spatial sandwich sampling | 0.1513 | −0.0036 | 1.0397 | 95.91 | 101.84 | 5.93 |
Comparing the errors of the three types of sampling results of annual precipitation,the mean error(ME)of the spatial sandwich sampling was 0.1513,the nearest to 0; the −2.0870 error of the spatial random sampling was the largest,indicating that the arithmetic mean of all the prediction errors of the spatial random samples was the minimum. According to RMSE,ASE and |RMSE−ASE|,the interpolation result of the spatial sandwich samples was closest to the real level. The mean standardized error(MSE)of the spatial sandwich samples was closest to 0,followed by stratified samples and spatial random samples; this indicated that in the spatial sandwich sampling,the degree of difference between the sample mean and the population mean was the lowest. Standardization of root mean square standardized error(RMSSE)indicated the effectiveness of the standard deviation of the prediction value. If the standard error of prediction is valid,RMSSE should be close to 1. If RMSSE is greater than 1,then the prediction of variability is underestimated,and if RMSSE less than 1,then the predicted variability is overestimated. Here,the RMSSE of the spatial sandwich sampling was 1.0397,which was closest to 1,indicating that its predicted variability was the most valid.
Considering the capacity of all the stations,the optimal error index of all the stations showed the highest prediction accuracy. The interpolation prediction accuracy of the spatial random samples was the optimal,followed by spatial stratified sampling; spatial random sampling had the worst result.
The predicted values of the 155 stations interpolated by the 85 different samples were compared with the observed annual precipitation values at the 155 stations. Figure 4 is scatter diagram of the observed values and predicted values; three abnormal values were discarded. The regression coefficient and the correlation efficient of the spatial random sampling were 0.893 and 0.9437,respectively,indicating that the spatial random samples had the highest prediction accuracy.
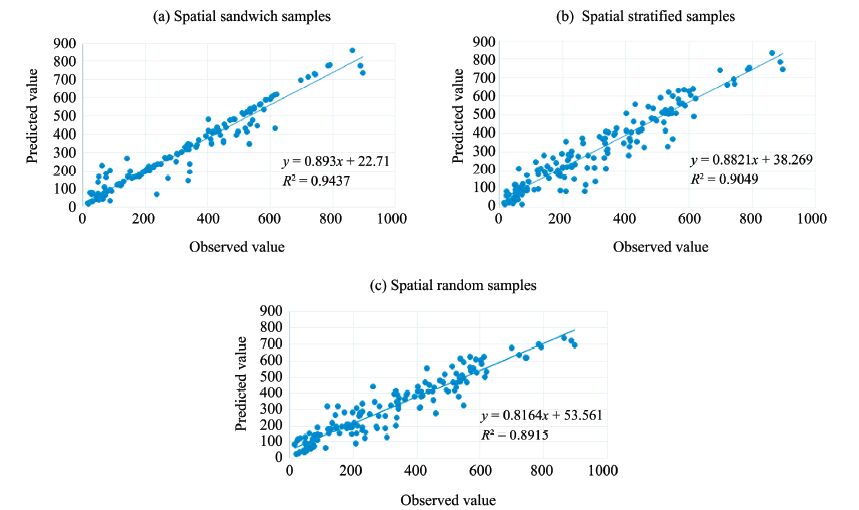
|
| Figure 4 Scatter diagram of observed values and predicted values at 152 stations |
According to the interpolation error calculation method of leave-one-out cross-validation,and the scatter diagram of predicted values and observed values,the correlation efficiency of the spatial sandwich samples was 0.9437,which was closer to 1 than were the spatial stratified samples and the spatial random samples. Thus,the spatial sandwich samples had greater representativeness than the two other types.
In order to verify the precipitation interpolation of the sample stations in rainy years and dry years,the sample stations were used to interpolate surface precipitation in a rainy year(2007) and a dry year(2008). The interpolation results and error of cross-validation are shown in Table 3 and Figure 5,respectively. The spatial random samples estimated well in the middle area of moderate precipitation,but performed badly in the southeast in 2007 and in both the southeast and northwest in 2008. Spatial stratified samples performed better in the southeast than did spatial random samples in both rainy years and dry years,but worse in the middle area in 2008. Spatial sandwich samples estimated the high values in both the southeast and northwest in the rainy year(2007) and dry year(2008),but did not perform better than spatial random samples at southern Xinjiang,northern Qinghai,and northeastern Gansu which had the least precipitation. Generally speaking,the spatial sandwich samples performed better than the other two methods in both the north and the south.
| Sampling methods | ME | MSE | RMSSE | RMSE | ASE | |RMSE−ASE| |
| All stations (2007) | 0.0682 | 0.002 | 0.9598 | 103.17 | 114.55 | 11.38 |
| Spatial random sampling | 0.2548 | −0.0053 | 0.9245 | 110 | 125.59 | 15.59 |
| Spatial stratified sampling | 0.0703 | 0.0036 | 1.0516 | 118.4 | 112.67 | 5.73 |
| Spatial sandwich sampling | 0.4035 | −0.0003 | 1.0751 | 115.43 | 111.71 | 3.72 |
| All stations (2008) | −0.8634 | −0.0063 | 0.9274 | 84.17 | 97.77 | 13.6 |
| Spatialrandomsampling | 0.1825 | 0.0003 | 0.8422 | 93.22 | 113.65 | 20.43 |
| Spatial stratified sampling | −0.9075 | −0.0015 | 0.9059 | 108.87 | 122.95 | 14.08 |
| Spatial sandwich sampling | −0.1510 | 0.0017 | 0.909 | 102.63 | 116.64 | 14.01 |
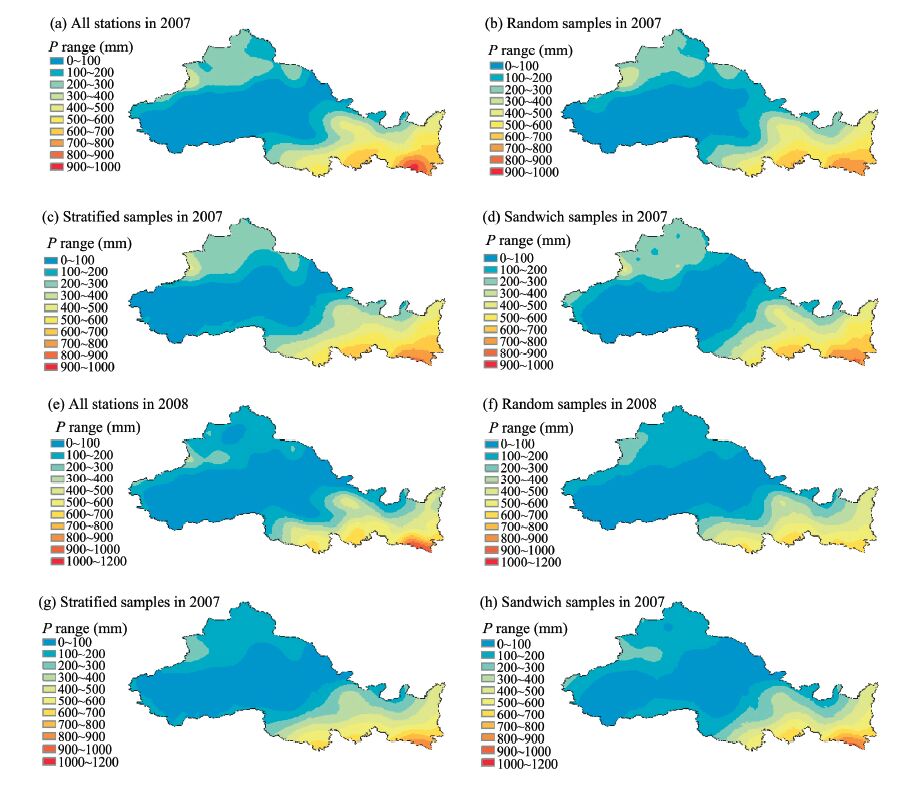
|
| Figure 5 The ordinary Kriging interpolation of precipitation under different distributions of sample points in 2007 (rainy year) and 2008 (dry year) |
However,according to the error of cross-validation,the spatial sandwich samples did not perform much better than spatial random samples in the dry year(2008). Therefore,we think spatial sandwich samples gave a better estimation of annual precipitation and performed well regarding extreme values among the average years,dry years,and rainy years.
4 ConclusionIn the sampling investigation of regional annual precipitation,the spatial random sampling method,the spatial stratified sampling method,and the spatial sandwich sampling method were set at the same sample size,and the sampling efficiency was measured by evaluating the precision of ordinary Kriging interpolation. We found that the spatial sandwich sampling method had the highest sampling efficiency,followed by the spatial stratified sampling method,and the spatial random sampling method did the worst. The spatial sandwich sampling and spatial stratified sampling fully considered the prior knowledge of people in the study area,while the spatial sandwich sampling imported the report layer,making the sampling results adjust to the report layer. Also,spatial sandwich sampling could report the information in the report layer according to the user's need.
The alpine zone of northwestern China is cold and sparsely populated,making it difficult to collect precipitation data and do other scientific research. Therefore,when we set up the rain gauges in the glacier basin,we cut down the number of gauges and the representativeness was improved by adopting the spatial sandwich sampling method. This suggests that optimization of the existing meteorological stations,for example,by using 85 representative spatial sandwich samples,performed better than other groupings. There are,however,some problems in this study. For example,the acquisition of the knowledge layer was difficult,and it will be necessary to acquire additional information and visit the study site to increase awareness of the study area. The spatial sandwich sampling only showed its superiority in the estimation of regional annual precipitation.
Acknowledgments:This research was conducted within the National Major Scientific Research Project(No. 2013CBA01806),the National Natural Science Foundation of China(No. 41271085),and the National Scientific and Technological Support Project(No. 2013BAB05B03). The precipitation data were downloaded from the China Meteorological Data Sharing Service System(http://www.cma.gov.cn/). We thank the National Climate Center of China for its data support.
| Alvarez O, Guo Q, Robert CK, et al, 2014. Comparison of elevation and remote sensing derived products as auxiliary data for climate surface interpolation. International Journal of Climatology, 34: 2258–2268. doi: 10.1002/joc.3835 |
| Ashiq MW, Zhao C, Ni J, et al, 2010. GIS-based high-resolution spatial interpolation of precipitation in mountain-plain areas of Upper Pakistan for regional climate change impact studies. Theoretical and Applied Climatology, 99: 239–253. doi: 10.1007/s00704-009-0140-y |
| Bostan PA, Heuvelink GBM, Akyurek SZ, 2012. Comparison of regression and Kriging techniques for mapping the average annual precipitation of Turkey. International Journal of Applied Earth Observation and Geoinformation, 19: 115–126. doi: 10.1016/j.jag.2012.04.010 |
| Cao ZD, Wang JF, Li LF, et al, 2008. Strata efficiency and optimization strategy of stratified sampling on spatial population. Progress in Geography, 27(3): 152–160. |
| Chen D, Ou T, Gong L, et al, 2010. Spatial interpolation of daily precipitation in China: 1951-2005. Advances in Atmospheric Sciences, 27(6): 1221–1232. doi: 10.1007/s00376-010-9151-y |
| Chen FX, Dai H, Hu YM, et al, 2012. Study on regional soil spatial sampling method. Geography and Geo-Information Science, 28(6): 53–56. |
| Chu SL, Zhou ZY, Yuan L, 2008. Study on spatial precipitation interpolation method: A case of Gansu province. Pratacultural Science, 25(6): 19–23. |
| Cochran WG, 1977. Sampling Techniques, 3rd edition. New York: Wiley,. |
| Fang SM, Qian ZT, Li YP, 2005. Comparison of four precipitation spatial interpolation methods in Gansu. Journal of Arid Land Resources and Environment, 19(3): 47–50. |
| He Y, Fu DP, Zhao ZM, et al, 2008. Analysis of spatial interpolation methods to precipitation based on GIS in Xinjiang. Research of Soil and Water Conservation, 15(6): 35–37. |
| Jiang CS, Wang JF, Cao ZD, 2008. A review of geo-spatial sampling theory. Acta Geographica Sinica, 64(3): 368–380. |
| Johnston K, VerHoef JM, Krivoruchko K, et al, 2001. Using ArcGIS Geostatistical Analyst- GIS by ESRI. United States of America Johnston,. |
| Kong YF, Tong WW, 2008. Spatial exploration and interpolation of the surface precipitation data. Geographical Research, 27(5): 1098–1108. |
| Krige DG, 1966. Two dimensional weighted moving average trend surfaces for ore-evaluation. Journal of the South African Institute of Mining and Metallurgy, 66: 13–38. |
| Liu XF, Pan YZ, Zhang JS, et al, 2013. Spatiotemporal variation patterns of potential evapotranspiration in five provinces of Northwest China in 1960-2011. Chinese Journal of Applied Ecology, 24(9): 2564–2570. |
| Lloyd CD, 2005. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. Journal of Hydrology, 308: 128–150. doi: 10.1016/j.jhydrol.2004.10.026 |
| Meng XJ, Zhang SF, Zhang YY, 2012. The temporal and spatial change of temperature and precipitation in Hexi Corridor in recent 57 years. Acta Geographica Sinica, 67(11): 1482–1492. |
| Moran PAP, 1948. The interpretation of statistical maps. Journal of the Royal Statistical Society (B), 37: 243–251. |
| Moran PAP, 1950. Notes on continuous stochastic phenomena. Biometrika, 37: 17–33. doi: 10.1093/biomet/37.1-2.17 |
| Rui XF, 2004. Principles of Hydrology. Beijing: China Water Power Press. |
| Shen YJ, Li S, Chen YN, et al, 2013. Estimation of regional irrigation water requirement and water supply risk in the arid region of Northwestern China 1989-2010. Agricultural Water Management, 128: 55–64. doi: 10.1016/j.agwat.2013.06.014 |
| Shi YF, Shen YP, Hu RJ, 2002. Preliminary study on signal impact and foreground of climatic shift from warm-dry to warm-humid in Northwest China. Journal of Glaciology and Geocryology, 24(3): 219–226. |
| Sun Y, Kang S, Li F, et al, 2009. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of Northwest China. Environmental Modelling & Software, 24: 1163–1170. doi: 10.1016/j.envsoft.2009.03.009 |
| Tobler WR, 1970. A computer movie simulating urban growth in the Detroit region. Economic Geography, 46(20): 234–240. doi: 10.2307/143141 |
| Tobler WR, 2004. On the first law of geography: A reply. Annals of the Association of American Geographers, 94(2): 304–310. doi: 10.1111/j.1467-8306.2004.09402009.x |
| Wang JF, Jiang CS, Li LF, 2009. Spatial Sampling and Statistical Inference. Beijing: Science Press. |
| Wang JF, Rui HN, Liu TJ, et al, 2013. Sandwich spatial estimation for multi-unit reporting on a stratified heterogeneous surface. Environment and Planning A, 45(10): 2515–2534. doi: 10.1068/a44710 |
| Wang JF, Zhuang DF, Li LF, 2002. Spatial sampling design for monitoring the area of cultivated land. International Journal of Remote Sensing, 13(2): 263–284. doi: 10.1080/01431160010025998 |
| Wang QX, Fan XH, Qin ZD, et al, 2012. Change trends of temperature and precipitation in the Loess Plateau Region of China, 1961-2010. Global and Planetary Change, 92-93: 138–147. doi: 10.1016/j.gloplacha.2012.05.010 |
| Wang S, Huang GH, Lin QG, et al, 2014. Comparison of interpolation methods for estimating spatial distribution of precipitation in Ontario, Canada. International Journal of Climatology, 34: 3745–3751. doi: 10.1002/joc.3941 |
| Wei H, Lia JL, Liang TG, 2005. Study on the estimation of precipitation resources for rainwater harvesting agriculture in semi-arid land of China. Agricultural Water Management, 71: 33–45. doi: 10.1016/j.agwat.2004.07.002 |
| Yavuz H, ErdoğanS, 2012. Spatial analysis of monthly and annual precipitation trends in Turkey. Water Resource Management, 26: 609–621. doi: 10.1007/s11269-011-9935-6 |
| Zhang JL, Zhang Y, 2011. The research of spatial sampling method of forest land area. Journal of Shandong Forestry Science and Technology, 2(6): 14–17. |
| Zhang SL, Zhang K, 2007. Comparison between general Moran's index and Getis-Ord general G of spatial autocorrelation. Acta Scientiarum Naturalium Universitatis Sunyatseni, 46(4): 93–97. |
 2016, 8
2016, 8


