Article Information
- ZhongQiong Zhang, QingBai Wu, Peng Zhang, SiRu Gao . 2016.
- Calculation method for thickness of discontinuous boundary layer of engineering pavement
- Sciences in Cold and Arid Regions, 8(6): 461-466
- http://dx.doi.org/10.3724/SP.J.1226.2016.00461
Article History
- Received: June 12, 2016
- Accepted: August 17, 2016
2. Beiluhe Observation Station of Frozen Soil Environment and Engineering, Northwest Institute of Eco-environment and Resources, Chinese Academy of Sciences, Lanzhou, Gansu 730000, China
The boundary layer,mainly below the ground surface,is attached to the ground surface and within it the vertical hydrothermal change is discontinuous (Zhu,1988). The thickness of the boundary layer is usually several tens of centimeters. Hydrothermal changes in this layer have direct effects on the change of water and heat in the active layer and permafrost(Jiang et al.,2012,2015; Li et al.,2013). In addition,the boundary layer thickness and temperature increment have very important influences on permafrost temperature analysis(Bai et al.,2015),especially in long-term permafrost temperature field studies(Cao et al.,2014).
> In previous permafrost thermal study procedures, the boundary layer was simplified into a thin layer, while the water and heat presented discontinuities in the cross section. Given measured ground temperature data,the temperature at 50-cm below the surface is usually considered as the stability hydrothermal bound,and this depth is often used for analyzing the temperature field(Wang et al.,2003; Dong et al., 2014). The complex hydrothermal changes in the boundary layer are generally not considered,and the scope of the boundary layer is,in fact,not fixed. Scholars have analyzed the thickness and ground temperature changes of the boundary layer from a theoretical perspective,continuously(i.e.,assuming no discontinuities in the cross section). Based on engineering thermal physics and harmonic theory,Zhu,(1988)determined that the thicknesses of the Boundary Layer Below Surface(BLBS)under asphalt pavement and dried sand-gravel soil were 35 cm and 30 cm,respectively(Zhu,1988). This result provided a relatively stable thermal boundary and improved the analysis accuracy(Woo et al.,2004). Then,based on energy balance law and the thermal transfer regime between the boundary layer and permafrost discontinuous interface,Li et al.(2006)applied the integral principle and integral median theorem to derive the joining condition of the thermal discontinuous interface. In order to obtain the dynamic boundary,scholars researched equivalent thermal diffusivity and derived formulae on the thickness and bottom temperature increment of the boundary layer(Bai et al.,2015); they then achieved good results in long-term, one-dimensional field temperature simulations. Therefore,a more accurate description of the boundary layer thickness will improve the accuracy of permafrost thermal state analysis.
By the atmospheric boundary layer and heat transfer theory,we established a calculation method for the boundary layer thickness,and discussed its rationality. The main contents are:(1)calculation of the thickness of the Boundary Layer Above Surface (BLAS)and explanation of its variation over a year; (2)our proposed average temperature attenuation coefficient (α)and calculation of the thickness of the BLBS,and explanation of its variation over a year; and (3)a discussion of the rationality of this method.
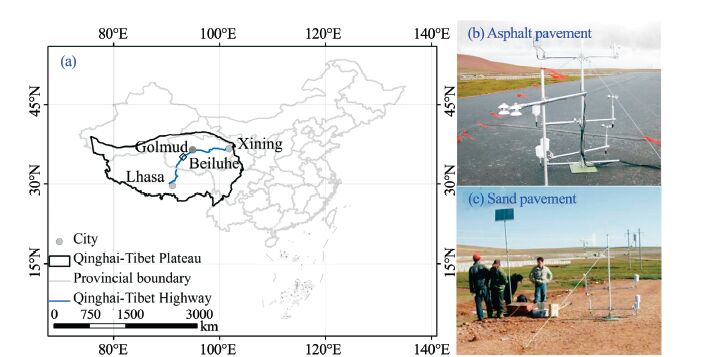
2 Data and methods 2.1 Data measurementsThe data were obtained from two engineering pavement(asphalt and sand pavement)sites in the southern Beiluhe Basin(34.82°N–34.85°N, 92.92°E–92.93°E)on the Qinghai-Tibet Plateau(Figure 1). Generally,the soil in the basin begins to thaw in April or May,and freezes in October or November, frozen period was about 5~6 months in a year. The test embankment we studied was 13 m wide and 3 m in height,and the asphalt pavement was 0.09 m thick, including 0.04 m of AC-13 fine-grain-modified asphalt mixture and 0.05 m of AC-16 modified asphalt mixture.The sand pavement was covered by coarse sand; there was no surface layer structure.
|
| Figure 1 Schematic of observation points |
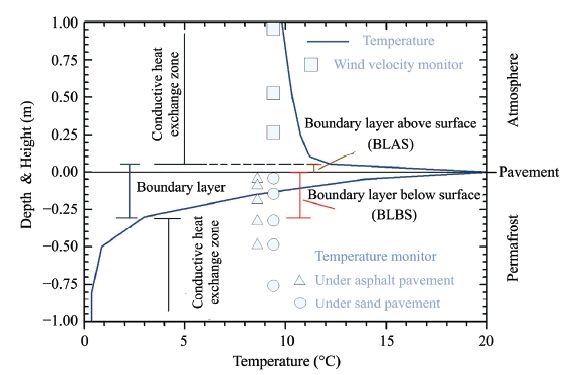
The data used in this study included soil temperature, wind velocity,and soil heat flux. Wind velocity was measured with a 010C/034B sensor(Met One Co., Oregon,U.S.A.),installed at heights of 0.25,0.50,and 1.00 m above the pavement surface(Figure 2). The sensor had a solution of 0.1 m/s and was used to calculate the BLAS. The soil temperature was tested with thermistors made by the State Key Laboratory of Frozen Soil Engineering,Chinese Academy of Sciences (SKLFSE),with sensitivity of ±0.05 ℃. Temperature sensors were installed at depths of 0.05,0.15,0.30, 0.50,and 0.80 m under the sand pavement,and 0.05, 0.10,0.15,0.20,0.30,0.50 m under the asphalt pavement (Figure 2). Soil heat flux was tested with an HFP01SC-10 heat flux sensor(Hukseflux Co.,Delft, The Netherlands),having a self-calibration function and resolution of ±3%. It was used to analyze the BLBS.
|
| Figure 2 Schematic of boundary layer and observation points |
A CR3000 data logger(Campbell Co.,Logan, U.S.A.)was used to collect and store the data; every 30 min the machine automatically generated a set of average values. Monitored data recorded from January 2014 to December 2014 were used in this paper.
2.2 Calculation method 2.2.1 The BLAS thickness The BLAS thickness is 1.18 times of the laminar layer height(Lykov,1961). According to the atmospheric boundary layer theory(Bagnold,1981),the laminar layer height was calculated by Equation(1)as below. The wind velocity at different heights could be fitted by the logarithmic function to get coefficients a, b,and obtain the laminar layer height(Z0); then the BLAS thickness could be obtained.| $\left\{ \begin{align} & {{u}_{t}}=a+\ln z \\ & {{Z}_{0}}=\exp \left( -a/b \right) \\ \end{align} \right.$ | (1) |
| $\frac{\partial T}{\partial t}=k\frac{{{\partial }^{2}}T}{\partial {{t}^{2}}}+\frac{{{C}_{w}}}{{{C}_{g}}}w\theta \frac{\partial T}{\partial z}$ | (2) |
| $\begin{align} & T\left( z,t \right)=\bar{T}\left( z \right)+A\exp \left[ -M\left( z-{{z}_{1}} \right) \right]\times \\ & \sin \left[ \omega t+{{\varphi }_{1}}-N\left( z-{{z}_{1}} \right) \right] \\ \end{align}$ | (3) |
| $\begin{align} & T\left( z,t \right)=\bar{T}\left( z \right)+A\exp \left[ -M\left( z-{{z}_{1}} \right) \right]\times \\ & \sin \left[ \omega t+{{\varphi }_{1}}-N\left( z-{{z}_{1}} \right) \right] \\ & M=\frac{W}{2k}+\frac{\sqrt{2}}{4k}\sqrt{{{W}^{2}}+\sqrt{{{W}^{4}}+16{{k}^{2}}{{\omega }^{2}}}} \\ & N=\frac{\sqrt{2}\omega }{\sqrt{{{W}^{2}}+\sqrt{{{W}^{4}}+16{{k}^{2}}{{\omega }^{2}}}}} \\ \end{align}$ |
|
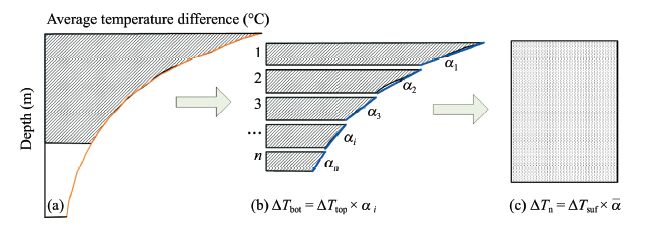
| Figure 3 Calculation schematic of the average attenuation coefficient (α) |
| $T\left( z \right)=\bar{T}\left( z \right)A\bar{\alpha }$ | (4) |
| $\bar{\alpha }={{A}_{1}}\exp \frac{z}{{{t}_{1}}}+{{y}_{0}}$ | (5) |
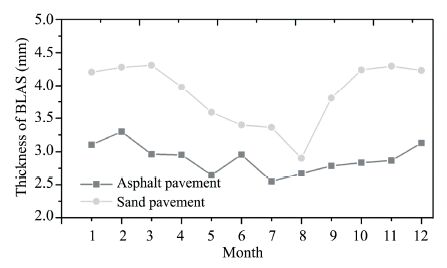
The BLAS thickness was calculated through the wind velocity. Figure 4 shows the monthly changes of the BLAS thickness; it was relatively thick in the cold season and thin in the warm season. The BLAS thickness of the sand pavement was greater than that of the asphalt pavement. For the asphalt pavement,the minimum was 2.55 mm in July and the maximum was 3.29 mm in February,with an average of 2.9 mm. For the sand pavement,the minimum was 2.9 mm in August and the maximum was 4.31 mm in March,with an average of 3.88 mm. In the warm season,the surface convection was greater than in the cold season,because turbulence easily formed above the bare surface. Meanwhile,the laminar layer thickness was reduced and the hydrothermal exchange rate within the layer was increased correspondingly. This directly affected the BLBS temperature and thickness(Sec. 3.2).
|
| Figure 4 Changes in the BLAS thickness |
Using the measured soil temperature data,we calculated the average monthly temperature amplitude and BLBS thickness. The average monthly temperature amplitude varied between 4.10~13.01 ℃ under the sand pavement,and 21.7~36.7 ℃ under the asphalt pavement. Figure 5 shows the changes in the BLBS thickness. The BLBS was thin in the cold season and thick in the warm season,and that of the asphalt pavement was greater than that of the sand pavement. For the asphalt pavement,the minimum was 28.2 cm in March and the maximum was 43.6 cm in July,with an average of 37.2 cm. For the sand pavement,the minimum was 15.8 cm in April and the maximum was 41.7 cm in July,with an average of 27.6 cm. The minimum generally appeared during the thawing process(March or April)and the freezing process(October or November), while the greatest thickness was reached between May and September. The soil phase change process(from solid to liquid,liquid to solid)consumed considerable energy; when the energy involved in the heat transfer was reduced,the BLBS was relatively reduced. In the thawing stage,when solar radiation had great intensity and transported much heat into the soil, the BLBS was increased. Because the thermal conductivity of frozen soil is about twice that of thawed soil,the BLBS would also increase.
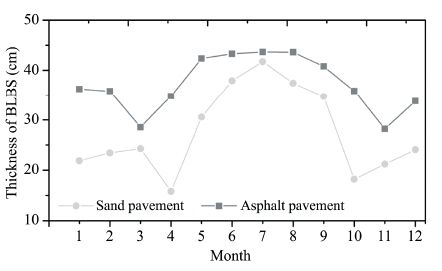
|
| Figure 5 Changes in the BLBS thickness |
The daily cycle is an important property of the boundary layer. The temperature peak and trough can occur in one day,with little change in time interval. Figure 6 shows the daily distribution of the daily maximum and minimum ground temperatures at the study site.
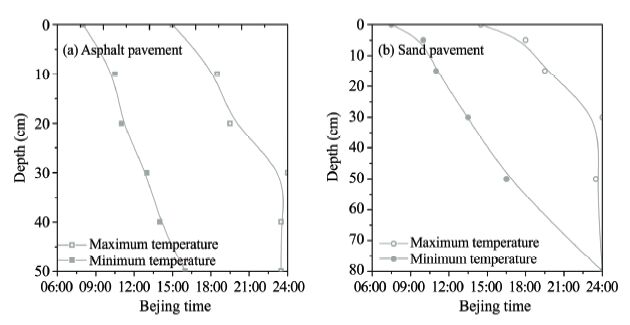
|
| Figure 6 Daily distribution of maximum and minimum ground temperatures under the pavements |
For asphalt pavement,the maximum and minimum temperatures appeared at 15:00 and 08:00,respectively, at the surface; the time span was 7 hours. At the 30-cm depth,the maximum temperature appeared at 23:30–24:00,and the minimum temperature was at 12:30–13:00. At the 50-cm depth,the maximum temperature appeared at 23:30–24:00,and the minimum temperature was at 16:00–16:30. For sand pavement, the maximum temperature appeared at 14:30 and the minimum temperature appeared at 07:00–07:30. At the 30-cm depth,the maximum and minimum appeared at 23:30–24:00 and 13:00–13:30,respectively. The appearing time of the maximum and the minimum were similar at the depth of 78 cm. As the depth increased beyond 30 cm,the temperature symmetry with the daily cycle gradually disappeared. When it was completely free from the influence of solar radiation,the BLBS thickness was less than 50 cm. So these results were quite reasonable.
4.2 The boundary layer and heat fluxThe boundary layer thickness may reflect the intensity of heat transfer. The thicker the BLAS is,the greater the turbulence intensity and sensible heat flux are. Compared with sand pavement,there were smaller changes in latent heat flux on the asphalt pavement over a year,and the total amount was also smaller.
Figure 7 shows the relationship between soil heat flux and soil temperature at the 5-cm depth below the pavement surface. Soil heat flux and temperature showed a linear relationship under the asphalt pavement; when the temperature rose by 2 ℃,the soil heat flux increased by about 0.94 W/m2. In contrast,soil heat flux and temperature showed a secondary polynomial relationship under the sand pavement. When the temperature rose by 2 ℃,the soil heat flux increased by about 3.74 W/m2. The average net radiation flux(Rn)values were 86.4 and 75.9 W/m2 above the asphalt and sand pavement,respectively(Zhang et al., 2016). Soil heat flux at the bottom of BLBS was small, less than 0.05 times of Rn. Thus,we concluded that this method can provide a more stable upper boundary for the temperature field analysis.
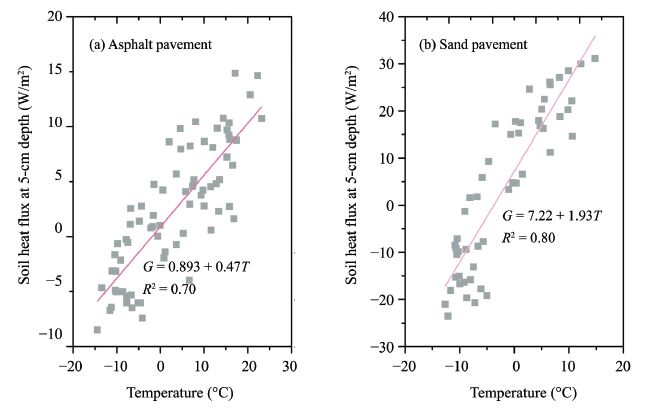
|
| Figure 7 The relationship between soil heat flux (G) and temperature (T) at 5-cm depth under pavements |
Based on continuous in-situ monitoring data on soil temperature,wind velocity,and soil heat flux,the thicknesses of BLAS and BLBS were calculated by a novel method proposed in this paper. The method was based on atmospheric boundary layer theory and the heat transfer theory. The BLAS was thick in the cold season and thin in the warm season. The BLBS was thin in the freezing and thawing processes but was relatively thicker in the freezing stage; the maximum thickness appeared in the thawing stage. For asphalt pavement,the BLAS thickness varied between 2.90 and 4.31 mm and the BLBS varied between 28.00 and 45.38 cm. For sand pavement,the BLAS thickness varied between 2.55 and 3.29 mm and the BLBS varied between 15.00 and 46.44 cm. Regarding daily cycles and soil heat flux,analysis of ground temperature changes revealed that the Soil heat flux at the bottom of BLBS was less than 0.05 times to that of Rn. The symmetry of the heat flux and the daily temperature cycle disappeared at depths beyond 30 cm. The boundary layer thickness calculation method presented in this paper can thus provide a more stable upper boundary for temperature field analysis.
Acknowledgments:This research was supported by the Natural Science Foundation of China(41330634 and 41301071),and the Independent Research Project of State Key Laboratory of Frozen Soil Engineering(SKLFSE-ZQ-19). We would like to express our sincerest gratitude to the anonymous reviewers for providing us with constructive and insightful comments and suggestions.
| Bagnold RA, 1981. The Physics of Blown and Desert Dunes. New York: Methuen: 85-95. |
| Bai QB, Li X, Tian YH, 2015. Upper boundary conditions in long-term thermal simulation of subgrade. Chinese Journal of Geotechnical Engineering, 37(6): 1142–1149. |
| Cao YB, Sheng Y, Wu JC, et al, 2014. Influence of upper boundary conditions on simulated ground temperature field in permafrost regions. Journal of Glaciology and Geocryology, 36(4): 802–810. |
| Dong YH, Pei WS, Liu G, et al, 2014. In-situ experimental and numerical investigation on the cooling effect of a multi-lane embankment with combined crushed-rock interlayer and ventilated ducts in permafrost regions. Cold Regions Science and Technology, 104-105: 97–105. doi: 10.1016/j.coldregions.2014.05.003 |
| Gao ZQ, 2005. Determination of soil heat flux in a Tibetan short-grass prairie. Boundary-Layer Meteorology, 114: 165–178. doi: 10.1007/s10546-004-8661-5 |
| Jiang Y, Zhuang Q, O'Donnell JA, 2012. Modeling thermal dynamics of active layer soils and near-surface permafrost using a fully coupled water and heat transport model. Journal Geophysical Research, 117(D11): 90–100. doi: 10.1029/2012JD017512 |
| Jiang Y, Rocha AV, O'Donnell JA, et al, 2015. Contrasting soil thermal responses to fire in Alaskan tundra and boreal forest. Journal of Geophysical Research Earth Surface, 120: 363–378. doi: 10.1002/2014JF003180 |
| Li NS, Hu WW, Wu QB, et al, 2006. Disposal of discontinuous thermal interface in calculation of temperature field of permafrost. Journal of Tongji University (Natural Science), 34(8): 1011–1015. |
| Li R, Zhao L, Ding YJ, et al, 2013. Study on soil thermodynamic characteristic at different underling surface in northern Qinghai-Tibet Plateau. Acta Energiae Solaris Sinica, 34(6): 1076–1084. |
| Lykov AV, 1961. Minsk: The Belarusian Academy of Sciences Press. : 56-59. |
| Wang TH, Hu CS, Li N, et al, 2003. Science in China (Series E). : 655-662. |
| Williams PJ, Smith MW, 1989. The Frozen Earth: Fundamentals of Geocryology. Cambridge, New York: Cambridge University Press: 306. |
| Woo MK, Arain MA, Mollinga M, et al, 2004. A two-directional freeze and thaw algorithm for hydrologic and land surface modeling. Geophysical Research Letters, 31(12): 261–268. doi: 10.1029/2004GL019475 |
| Zhang ZQ, Wu QB, Xun XY, 2016. Radiation and energy balance characteristics of asphalt pavement in permafrost regions. Environment Earth Science, 75(3): 1–19. doi: 10.1007/s12665-015-4975-5 |
| Zhu LN, 1988. Study of the boundary layer on different types of ground in permafrost regions on the Qinghai-Xizang Plateau. Journal of Glaciology and Geocryology, 10(1): 35–39. |
 2016, 8
2016, 8


