Article Information
- JunJun Yang, ZhiBin He, WeiJun Zhao, Jun Du, LongFei Chen, Xi Zhu. 2016.
- Assessing artificial neural networks coupled with wavelet analysis for multi-layer soil moisture dynamics prediction
- Sciences in Cold and Arid Regions, 8(2): 116-124
- http://dx.doi.org/10.3724/SP.J.1226.2016.00116
Article History
- Received: June 24, 2015
- Accepted: September 2, 2015
2. Academy of Water Resources Conservation Forests in Qilian Mountains of Gansu Province, Zhangye, Gansu 734000, China;
3. College of Forestry, Gansu Agricultural University, Lanzhou, Gansu 730070, China
1 Introduction
Soil moisture is an essential prediction variable in global climate change research because it affects the flow of energy,greenhouse gases, and water among the atmosphere,vegetation, and soils(Wofsy et al., 1993; Kokaly and Clark, 1999; Klemas et al., 2014). In semi-arid ecosystems,dynamic information on soil moisture is critical to the underst and ing of hydrological processes for research application in meteorology,soil hydrology, and ecology(He et al., 2012), and for water management operations including estimation of groundwater recharge and monitoring of drought conditions(Dumedah et al., 2014). Hence,accurate simulations of the spatial and temporal dynamics of soil moisture conditions are critical to arid ecological systems at regional and local spatial scales.
Estimation of soil moisture can be accomplished in two ways. The first approach uses distribution or two-dimensional models,including physical-based process models(Chen et al., 2014) and remote sensing retrieval models(Qin et al., 2009). Physical models need substantial inputs of spatial parameters and sequential meteorological data. Remote sensing is prohibitively expensive and can only estimate near-surface soil moisture at low spatial resolutions(Al-Hamdan and Cruise, 2010); therefore,it is not practical to simulate multilayer soil moisture at small spatial scale. The second approach may be data-driven and uses forecasting tools such as the ensemble particle filter(Yu et al., 2012),with no physical infrastructure; it is easy to achieve. Unlike the data-driven approach,process-based models require sequential climate factors, and parameters of spatial soil properties and vegetation(Wu and Jansson, 2013). Therefore,these are not easy to use due to the need for acquisition of required parameters and continuity of high quality field data.
The development of models for describing such complex phenomena as the highly stochastic nature of hydrological processes is a growing area of research. The use of machine learning in hydrology has steadily increased,attracting more scientists to develop new models to forecast the non-linear hydrological processes(Tiwari et al., 2013; Dumedah et al., 2014; He et al., 2014). Despite the usefulness and flexibility of artificial neural networks(ANNs)in modeling hydrological processes,they have significant drawbacks of non-stationary response and lack of input/output data pre/post-processing. Therefore,coupling of models can comprise an important improvement. Presently,wavelet-transformation plays a vital role in data pre-procedure, and can reliably improve ANNs shortcomings in dealing with non-stationary behavior of input data.
A few studies have evaluated soil moisture using meteorological variables with data-driven models. Modeling of complex soil moisture dynamics for three reconstructed soil covers at three soil depths indicated that modeling of soil moisture using ANNs is challenging but achievable(Elshorbagy and Parasuraman, 2008). Deng et al.(2011)compared various nonlinear stochastic models(least-squares-support vector machine and ANN)in their ability to simulate soil moisture and chaotic time series analysis methods(wavelet decomposition methods)for pre-processing of original chaotic soil water signals; their results show that wavelet transformation had a low effect on the embedding dimension and that appropriate wavelet tendency information can improve the predicting capacity. Yu et al.(2012)used one year of meteorological data to estimate multi-layer soil moisture by coupling ensemble particle filter(EnPF)algorithm and support vector machines(SVMs); their study confirmed the usefulness of data assimilation technique(EnPF)in soil moisture prediction.
Semi-arid mountain regions have spatially-heterogeneous soil moisture and data quality is compromised by lack of stability and continuity. Therefore,an enhanced underst and ing of soil moisture temporal dynamics, and an improved ability to forecast are urgently needed to offset limited observations. Soil water is widely recognized as a resource capable of maintaining highly diverse and rich ecosystems in mountainous regions. Variations in soil water are mainly concentrated in the 0-200 cm depth,where bulk of plant roots is also distributed. Thus,accurate simulations of soil moisture dynamics in this zone are vital for predicting vegetation growth.
In this study,we tested the use of a developed coupled model(WA-ANN)of wavelet analysis(WA) and artificial neural network(ANN)for forecasting of multilayer soil moisture based only on multi-meteorological factors including temperature,net solar radiation,wind speed, and precipitation. Wavelet analysis had been set up to remove the noise(r and om variations) and inaccuracies of information, and to decompose non-stationary signal and produce estimates of unknown variables that tend to be more precise than the input data. The main objective of this study was to develop a simple daily soil moisture model WA-ANN to optimize the prediction capacity of ANN in soil water and heat simulation; we did this by coupling wavelet and ANN.
2 Methods 2.1 Artificial neural networkA neural network is a parallel-distributed processor consisting of simple processing units called neurons,which are nonlinear,parameterized,bounded functions that store experimental data and render them available for use(Haykin,1999; Dreyfus,2005); neural network may be viewed as an adaptive approach. Back-propagation,widely-used since its development by Rumelhart et al.(1986),minimizes error by comparing simulated outputs with observed values using a gradient-descent algorithm. Each unit's computation is divided into two components. First,the summation function calculates the weighted sum of the inputs. Second,nonlinear activation transforms the weighted sums to the final value.
The network is fully connected,that is,a neuron in any one layer of the network is connected to all the nodes in the other layers. Signal flow through the network is bidirectional; the function signals(weight/bias)transmit forward, and the error signals can propagate backward. The function signal is the input signal that enters at the input terminal of the network,propagates forward, and appears at the output terminal. An error signal generated at the output terminal transmits backward through the network,layer by layer.
Hidden neurons(layers between the input and the output layer that do not have any interaction with the environment are known as hidden neurons)are not part of the input or output of the network, and there are two computations involved. First,the function signal is computed,which is a continuous nonlinear function of the input signal, and synaptic weights associated with the neuron. Second,an estimate is computed as the gradient vector,needed for the backward pass through the network.
The error signal at the output of neuron i at iteration n can be defined as:
| ${e_i}(n) = {d_i}(n) - {y_i}(n) $ | (1) |
| $ \varepsilon (n) = \frac{1}{2}\sum\limits_{i = C} {e_i^2(n)} $ | (2) |
If we set N to denote the total number of patterns contained in the training set,the average squared error energy is acquired by summing ε(n)over all n and then normalizing with respect to the set size N,we may thus write
| ${\varepsilon _{av}} = \frac{1}{N}\sum\limits_{n = 1}^N {\varepsilon (n)} $ | (3) |
One of the main advantages of neural networks is the possibility of using multiple sources of data; this is because neural networks do not assume a statistical distribution of the input data(Brown et al., 2008).
2.2 Coupling of wavelet analysis and ANNWavelet analysis is widely applied because of its capacity to elucidate time-series characteristics both in frequency and temporal domains(Sang,2012). Noise in the observation series is generated from different environments and from physical mechanisms,so it varies in characteristics. The observation series and noise can be separated by using the wavelet method. As a combination,WA-ANN can reduce or remove noise,or the r and om and uncertain natural factors as well as the subjective factors in the input meteorological factors, and ANN can obtain a more accurate and reliable time series results for the input factors and the multi-layer soil water content. Just like other transformation techniques(e.g.,Fourier),the wavelet transformation also has its own critical factors. Two key issues,in particular,need attention in wavelet application; first is the choice of mother functions, and second is the choice of proper time scale levels(Sang et al., 2009).
Because the observation time series data are usually discrete,we chose a total of 54 wavelets,among them haar,daubechies,symlets,coiflets,biorthogonal,reverse biorthogonal, and meyer,as the optional functions(name of the functions are family members of wavelet,details can be found at Product Help document of Matlab R2010b). Biorthogonal(bior) and reverse-biorthogonal spline wavelet filter(rbio)mother-wavelet functions were screened for the optimal de-noising methodology. Both wavelet functions have some common characteristics,so they can compactly support biorthogonal spline wavelets for which symmetry and exact reconstruction are possible with FIR filters. The decomposition level had been determined by the maximum wavelet decomposition level function from the wavelet library function of Matlab R2010b for each wavelet(Sang and Wang, 2008). The heursure algorithm is one of the de-noising methods of synthesis version,based on both,the universal threshold and Stein's unbiased estimate of risk; detailed information can be found in Messer et al.(2001).
The task of the coupling is three-fold: first,noise of the observation series is removed through the wavelet, and the de-noised data are prepared as the input data; second,determine the optimal number of hidden layers and delay days using trial- and -error in sequence; third,simulate soil moisture and temperature based on the optimized parameters of ANN. The flow chart of the input data is depicted in Figure 1.
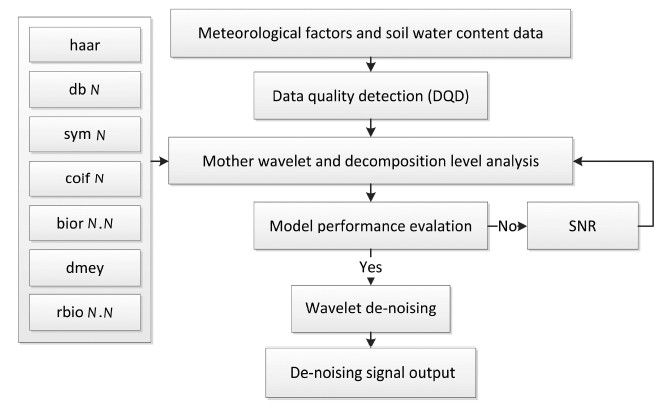
|
| Figure 1 Flow chart of the wavelet de-noising system. Note: haar (haar wavelet), db (daubechies wavelets), sym (symlets), coif (coiflets), bior (biorthogonal wavelets), dmey (discrete approximation of meyer wavelet), and rbio (reverse biorthogonal wavelets) |
The accuracy of the de-noised signal was evaluated by root mean square error(RMSE')(4) and signal to noise ratio(SNR)(5). SNR is an index used to compare the levels of a desired signal and the background noise. The greater the ratio,the lesser the noise, and the more easily it can be filtered out. In this study,we used SNR to choose a reasonable wavelet function by comparing the analysis results of the following wavelet functions:
| $ RMSE' = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({d_i} - {x_i})}^2}} } $ | (4) |
| $ SNR = 10.ln\left[ {\frac{{\sum\limits_{i = 1}^n {x_i^2} }}{{\sum\limits_{i = 1}^n {{{({d_i} - {x_i})}^2}} }}} \right] $ | (5) |
To avoid overlooking of useful predictors,we evaluated model performances in this study with five different types of st and ard statistical criteria(Latt and Wittenberg, 2014). These were coefficient of determination(R2)(6),root mean square error(RMSE)(7),mean absolute relative error(MARE)(8),the relative percent deviation to RMSE(RPD)(9) and Nash-Sutcliffe efficiency coefficient(NSE)(10).
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{({W_s} - {W_f})}^2}} }}{{\sum\limits_{i = 1}^n {{{({W_s} - {{\bar W}_s})}^2}} }} $ | (6) |
| $ RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{({W_o} - {W_s})}^2}} }}{n}} $ | (7) |
| $ MARE = \frac{{\sum\limits_{i = 1}^n {\left| {\frac{{{W_s} - {W_f}}}{{{W_s}}}} \right|} }}{n} $ | (8) |
| $ RPD = \frac{{{D_s}}}{{RMSE}},{D_s} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{({W_s} - {{\bar W}_s})}^2}} }}{{n - 1}}} $ | (9) |
| $ NSE = 1 - \frac{{\sum\limits_{i = 1}^n {{{[{{({W_o})}_i} - {{({W_s})}_i}]}^2}} }}{{\sum\limits_{i = 1}^n {{{[{{({W_o})}_i} - {{({{\bar W}_s})}_i}]}^2}} }} $ | (10) |
The NSE can range from −∞ to 1,with 1 meaning a perfect match of modeled signal to observed signal data; essentially,the closer the efficiency is to 1,the more accurate the model is. This index has been recommended for two major reasons: first,it is recommended by Legates and McCable(1999), and second it is commonly used(Moriasi et al., 2007). Further,the temporal dynamic of soil moisture plots was used as another way to analyze the effectiveness of the two techniques. Finally,to obtain clearly distinctive changes in precipitation,we used a cumulative precipitation of the real time series instead of the event rainfall.
3 Case study 3.1 Study areaData for this study were taken from the Pailugou catchment in the Qilian Mountains,located near Zhangye,Gansu Province,China(38°33'17"N,100°17'09"E)(Figure 2). The catchment has a total area of 2.91 km2. The main vegetation is a Picea crassifolia forest. Mean annual precipitation and temperature are 375.5 mm and 0.5 °C,respectively, and elevation is 2,700 m. Mean height of grasses is about 25 cm, and mean plant cover is about 90%(He et al., 2012). Two types of soil are prevalent in the area. The montane chestnut soil is distributed mainly on sunny exposures at elevations 2,720-3,000 m,with mean soil depth of about 40 cm,pH 8.0-8.5, and organic fraction of the surface soil of 2%-4%. The mountain forest grey brown soil is distributed mainly on shady exposure at elevations between 2,600 and 3,770 m,with mean soil depth of about 67 cm,pH 7.0-8.0,grass height of 20-30 cm, and organic fraction of the surface soil of 10%-25%. The shady(north-facing) and semi-shady(northwest-facing or northeast-facing)slopes are covered with P. crassifolia forest,while the sunny(south-facing) and semi-sunny(southwest-facing or southeast-facing)slopes are mainly occupied by grasses.
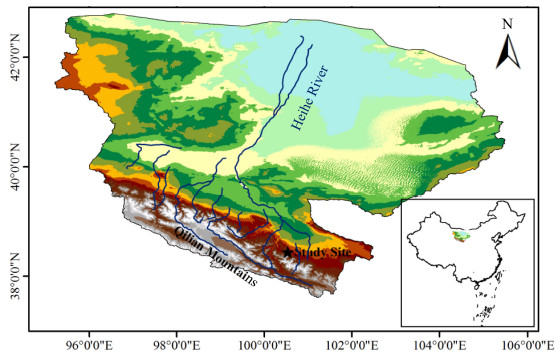
|
| Figure 2 Map of the study site. Background picture is Shuttle Radar Topography Mission (SRTM) DEM of Heihe River Basin |
Meteorological factors(air temperature,l and surface temperature,relative humidity,atmosphere pressure,wind speed,solar radiation and precipitation)are well known to affect soil water content, and they are typically used as the input variables in soil moisture prediction models. Input meteorological data for this study were obtained from IMKO's comprehensive weather station at half hour intervals. Soil water content data were obtained using time domain reflectometry(TDR)over the observation period, and recorded in half-hour intervals. Input meteorological and multi-layer soil water content data were de-noised with an appropriate wavelet function. Six probes were inserted horizontally in the middle of each soil layer:(a)20,(b)40,(c)60,(d)80,(e)120, and (f)160 cm. All data used were collected from January 20,2010 to November 30,2011. Data were preprocessed to daily values for this study,checked for any human or machine-caused errors, and submitted for the de-noising procedure. Observational period was separated as follows: training period from January 20 to December 31 in 2010, and validation period from January 1 to November 31 in 2011. All calculations were accomplished using Matlab R2010b(The Mathworks,Inc.,Natick,MA).
3.3 Model developmentANN coupled with the wavelet technique was used for daily estimation of soil moisture in six different soil layers,as described above. To be consistent with meteorological factors,the multi-layer soil water content had been de-noising before use. Before ANN simulation,the optimum number of neurons in the hidden layer and feedback delays was determined by a trial- and -error approach in a successive manner. The pre-defined range of hidden neurons was sampled from 2 to 20, and the feedback delays were searched between 1 and 20. The Leverberg-Marquardt(LM)method was used for the multi-layer perceptron in this study because it has been proven to be the fastest in training moderate-size feed-forward neural networks(Karul et al., 2000). Maximum NSE was used as the cross-validation method to select the most probable situation for the validation. The execution process of WA-ANN is depicted in Figure 3.
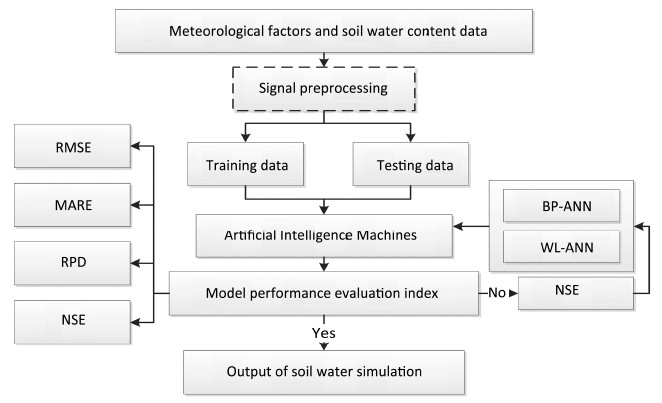
|
| Figure 3 The flow chart of soil water content prediction system. Note: RMSE (error of mean square), MARE (mean absolute relative error), RPD (relative percent deviation), NSE (nash-sutcliffe efficiency coefficient) |
The wavelet function,value of hidden neurons, and days of feedback delays are given in Tables 1 and Table 2. Based on different discrete wavelet transfer(DWT)functions,the same composition level 1 had been selected for the maximum SNR objective function using the trial- and -error experiments in input signal de-noising. The output signals tracked the observation data extremely closely. Differences were observed only at the inflection points of the curve of the observation data.
| Factor | Temperature mean 1.5 m | Land surface temperature | Humidity 1.5 m | Global radiation | Atmospheric pressure | Wind speed | Precipitation |
| Wavelet function | bior1.5 | rbio3.3 | bior1.3 | bior3.3 | bior3.3 | bior1.3 | rbio3.3 |
| Item | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | |
| Wavelet function | bior1.3 | bior1.5 | bior1.5 | rbio3.3 | bior3.3 | bior3.3 | |
| Number of the hidden neurons | 2 | 17 | 3 | 5 | 11 | 14 | |
| Number of feedback delay days | 11 | 2 | 9 | 7 | 5 | 5 | |
| Note: number of the hidden neurons and feedback delay days determined in ANN modeling for different soil. | |||||||
NSEs of training were all very close to 1(NSE > 0.995),hence we focused our attention on the validation results. Statistical indices of model validation of ANN and WA-ANN are summarized in Table 3.
| Function | Soil layer | R2 | RMSE | MARE | RPD | NSE |
| ANN | Layer 1 | 0.992 | 0.764 | 0.027 | 10.085 | 0.990 |
| Layer 2 | 0.998 | 0.400 | 0.011 | 21.069 | 0.998 | |
| Layer 3 | 0.999 | 0.162 | 0.006 | 53.547 | 0.999 | |
| Layer 4 | 0.991 | 0.665 | 0.025 | 10.570 | 0.991 | |
| Layer 5 | 0.999 | 0.123 | 0.004 | 21.120 | 0.998 | |
| Layer 6 | 0.965 | 0.623 | 0.010 | 1.855 | 0.856 | |
| WA-ANN | Layer 1 | 0.995 | 0.593 | 0.018 | 13.050 | 0.994 |
| Layer 2 | 0.997 | 0.488 | 0.018 | 17.233 | 0.997 | |
| Layer 3 | 0.999 | 0.254 | 0.008 | 34.066 | 0.999 | |
| Layer 4 | 0.995 | 0.474 | 0.018 | 14.812 | 0.995 | |
| Layer 5 | 0.999 | 0.082 | 0.004 | 33.087 | 0.999 | |
| Layer 6 | 0.989 | 0.314 | 0.007 | 4.398 | 0.962 |
These properties coincided with multidimensional non-stationary meteorological time series; the features of the wavelet itself was the key factor in the choice of the mother-wavelet selection, and these results were similar to those of Sang and Wang(2008). The decomposition level was 2,indicating that the wavelet functions had dealt with the noise of the input signal and ,at the same time,the post-processing series retained raw information to the highest possible(Coifman and Wickerhauser, 1992). The range of the decomposition level was determined between 1 and the maximum depending on the mother-wavelet, and the amount of the input time series. The method for confirming the decomposition level was more scientific and acceptable than what was proposed by the author's subjective attitude(Sang et al., 2009). Thus,we concluded that the de-noising results corresponded to time-series data, and this indicated the appropriateness of the method. Compared to the processed time series,the original observation sequence showed little noise with,r and om characteristics,most likely due to the continuity in the observation time series and equipment stability.
Once the reasonable mother-wavelet function and corresponding decomposition level had been identified,we investigated the statistical results of model validation to determine whether or not the de-noising technology was effective in the prediction of soil moisture. Subjected to the natural of ANN(each simulation of ANN is an independent and stochastic behavior),the hidden neurons were determined for the various soil water content layers(Table 1).
By comparing analysis results of the two stochastic prediction technologies ANN and WA-ANN,we detected the same trend in the validation results(Figure 4 and Table 3). First,ANN simulated the actual soil moisture time series with NSEs in most cases(Table 3), and the simulation curve coincided well with the observation line. This indicated applicability of ANN as one of the data-assimilation methods. We compared our results with Elshorbagy and Parasuraman(2008) and Sang et al.(2009). Second,some singular points(micro-mutations)were detected in the simulation line at the inflection points of the original time series,indicating that the model exaggerated these fluctuations and exhibited an adaptive process in the simulation(Figure 4). Here,ANN performed worse than WA-ANN, and this phenomenon was not replicated in the scatter plots(Elshorbagy and Parasuraman, 2008; Yu et al., 2012). This was an example of over-fitting phenomenon,in which ANN was too complex(too many hidden neurons) and reacted by amplifying the noise of the input data. Another explanation may be that the ratio of training to testing was not sufficient. We concluded that the reason was the ratio of model training to validation. The best way to avoid over-fitting is to have more training data(30 times more than the training series),but in practice,it is almost impossible to achieve so many observations in a time series. Nevertheless,we recommend extending the training time series to the maximum possible. Third,the two methods exhibited some differences in the simulations of soil water content in the deepest layer(160 cm),especially in the low-value interval. Here,both approaches performed greater than actual soil moisture values; these results were unlike those of Yu et al.(2012)who found no differences in the multi-layer's soil moisture prediction. The mostly likely reason for the differences of the two studies was greater precipitation observed at Yu et al.(2012)study site located in Jiangsu Province,with a corresponding strong response of soil moisture at the deepest layer to meteorological factors. The dynamics of soil moisture at the deepest soil layer(160 cm)in our study presented a relatively weak link with meteorological environmental factors because of small rainfall typical of our site. Thus,deep soil moisture in our study was not only affected by climate but also possibly by other factors,such as bed rock or frozen soil. Bedrock can stop the vertical transfer of soil moisture and frozen soil can redistribute heat and change the direction of transfer and the form of water simultaneously.
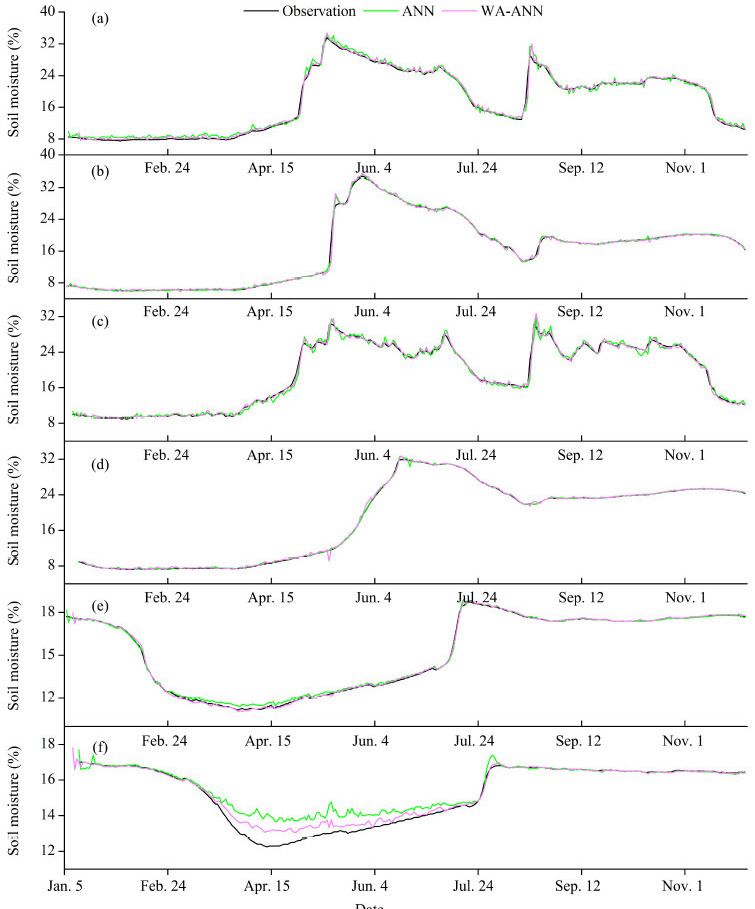
|
| Figure 4 Validation results of soil water content by ANN and WA-ANN from January 6, 2011 to November 31, 2011 |
The performance of the simulation at different soil depths may be used as an index of the depth at which meteorological factors interact with soil heat and water processes. Based on this,soil moisture at different soil depths should be independently processed in the simulation. WA-ANN performed better than ANN at the low value of the curve(its inflection point).
The aim of the de-noising technology is to reduce the noise as best as possible and ,at the same time,retain useful information of the original time series to the highest extent possible. We strove for the optimization of the prediction results without compromising the original time series; therefore,we chose to preserve raw information by using the assembly of maximum SNR and the one-dimensional automatic de-noising process of one-dimensional signal which uses heuristic variant of the threshold selection rule('heursure'). Based on the results of this study,we conclude that de-noising of the meteorological time series data was reasonable and accurate, and the new method used here is effective and feasible.
6 ConclusionsPrediction of soil moisture,especially in the root zone has attracted a great deal of interest all over the world. It is a major requirement in the ability to effectively predict hydrological processes such as flow and climate studies. In this study,we investigated the performance of ANN and WA-ANN, and optimized the related controlling parameters.
In prediction processes,heursure algorithms and wavelet decomposition were applied to preprocess the original time series signal. The maximum SNR was used for the evaluation of the de-noising algorithm, and the hidden neurons and delay-days of ANN were optimized with the trial- and -error method before model estimation. The over-fitting(singular point)phenomenon of ANNs should be resolved by redistributing the period of training and validation of the input data. In summary,the ensemble wavelet analysis and artificial neural networks can improve the predictive ability for multi-layer soil moisture.
Our main findings were as follows:(1)The ANN model performed very well in simulating soil moisture in the root zone and in the deepest soil layer,demonstrating the ability of ANNs to predict soil water content in a semi-arid region;(2)Wavelet de-noising technology showed high effectiveness in the simulation; WA-ANN improved the performance especially in the deepest soil layers.
Acknowledgments: We thank the reviewers for their helpful suggestions on improving this manuscript. This work was supported by funding from the Major Research Plan of National Natural Science Foundation of China(Grant No. 91225302). Furthermore,we acknowledge Wei Zhang for the improvements of the original program code. Special thanks go to Kathryn Piatek and XiaoHu Wen for revisions to this manuscript.| Al-Hamdan OZ, Cruise JF, 2010. Soil moisture profile development from surface observations by principle of maximum entropy. Journal of Hydrologic Engineering, 15(5):327-337. DOI:10.1061/(asce)he.1943-5584.0000196. |
| Brown ME, Lary DJ, Vrieling A, et al., 2008. Neural networks as a tool for constructing continuous NDVI time series from AVHRR and MODIS. International Journal of Remote Sensing, 29(24):7141-7158. DOI:10.1080/01431160802238435. |
| Chen M, Willgoose GR, Saco PM, 2014. Spatial prediction of temporal soil moisture dynamics using HYDRUS-1D.Hydrological Processes, 28(2):171-185. DOI:10.1002/hyp.9518. |
| Coifman RR, Wickerhauser MV, 1992. Entropy-based algorithms for best basis selection. IEEE Transactions on Information Theory, 38(2):713-718. DOI:10.1109/18.119732. |
| Deng JQ, Chen XM, Du ZJ, et al., 2011. Soil water simulation and predication using stochastic models based on LS-SVM for red soil region of China. Water Resources Management, 25(11):2823-2836. DOI:10.1007/s11269-011-9840-z. |
| Dreyfus G, 2005. Neural Networks Methodology and applications.ESPCI, Laboratoire d'Electronique 10 rue Vauquelin 75005 Paris, France. |
| Dumedah G, Walker JP, Chik L, 2014. Assessing artificial neural networks and statistical methods for infilling missing soil moisture records. Journal of Hydrology, 515:330-344. DOI:10.1016/j.jhydrol.2014.04.068. |
| Elshorbagy A, Parasuraman K, 2008. On the relevance of using artificial neural networks for estimating soil moisture content.Journal of Hydrology, 362(1-2):1-18. DOI:10.1016/j.jhydrol.2008.08.012. |
| Haykin S, 1999. Neural networks:A Comprehensive Foundation(2nd Edition). Sai PrintoPack Pvt. Ltd., Pearson Education(Singapore) Pte. Ltd., Indian Branch, 482 F. I. E. Patparganj, Delhi 110092, India. |
| He ZB, Wen XH, Liu H, et al., 2014. A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. Journal of Hydrology, 509:379-386. DOI:10.1016/j.jhydrol.2013.11.054. |
| He ZB, Zhao WZ, Liu H, et al., 2012. The response of soil moisture to rainfall event size in subalpine grassland and meadows in a semi-arid mountain range:A case study in northwestern China's Qilian Mountains. Journal of Hydrology, 420:183-190. DOI:10.1016/j.j.hydrol.2011.11.056. |
| Karul C, Soyupak S, Cilesiz AF, et al., 2000. Case studies on the use of neural networks in eutrophication modeling. Ecological Modelling, 134(2-3):145-152. DOI:10.1016/s0304-3800(00)00360-4. |
| Klemas V, Finkl CW, Kabbara N, 2014. Remote sensing of soil moisture:An overview in relation to coastal soils. Journal of Coastal Research, 30(4):685-696. DOI:10.2112/jcoastres-d-13-00072.1. |
| Kokaly RF, Clark RN, 1999. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sensing of Environment, 67(3):267-287. DOI:10.1016/s0034-4257(98)00084-4. |
| Latt ZZ, Wittenberg H, 2014. Improving flood forecasting in a developing country:A comparative study of stepwise multiple linear regression and artificial neural network. Water Resources Management, 28(8):2109-2128. DOI:10.1007/s11269-014-0600-8. |
| Legates DR, McCabe GJ, 1999. Evaluating the use of "goodness-of-fit" measures in hydrologic and hydroclimatic model validation. Water Resources Research, 35(1):233-241.DOI:10.1029/1998wr900018. |
| Messer SR, Agzarian J, Abbott D, 2001. Optimal wavelet denoising for phonocardiograms. Microelectronics Journal, 32(12):931-941. DOI:10.1016/s0026-2692(01)00095-7. |
| Moriasi DN, Arnold JG, Van Liew MW, et al., 2007. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Transactions of the ASABE, 50(3):885-900. |
| Qin J, Liang SL, Yang K, et al., 2009. Simultaneous estimation of both soil moisture and model parameters using particle filtering method through the assimilation of microwave signal. Journal of Geophysical Research-Atmospheres, 114:D15103. DOI:10.1029/2008jd011358. |
| Rumelhart DE, Hinton GE, Williams RJ, 1986. Learning representations by back-propagating errors. Nature, 323(6088):533-536. |
| Sang YF, 2012. A practical guide to discrete wavelet decomposition of hydrologic time series. Water Resources Management, 26(11):3345-3365. DOI:10.1007/s11269-012-0075-4. |
| Sang YF, Wang D, 2008. Wavelets selection method in hydrologic series wavelet analysis. Journal of Hydraulic Engineering, 39(3):295-300, 306. |
| Sang YF, Wang D, Wu JC, et al., 2009. Entropy-based wavelet de-noising method for time series analysis. Entropy, 11(4):1123-1147. DOI:10.3390/e11041123. |
| Tiwari MK, Song KY, Chatterjee C, et al., 2013. Improving reliability of river flow forecasting using neural networks, wavelets and self-organising maps. Journal of Hydroinformatics, 15(2):486-502. DOI:10.2166/hydro.2012.130. |
| Wofsy SC, Goulden ML, Munger JW, et al., 1993. Net exchange of CO2 in a midlatitude forest. Science, 260(5112):1314-1317.DOI:10.1126/science.260.5112.1314. |
| Wu SH, Jansson PE, 2013. Modelling soil temperature and moisture and corresponding seasonality of photosynthesis and transpiration in a boreal spruce ecosystem. Hydrology and Earth System Sciences, 17(2):735-749. DOI:10.5194/hess-17-735-2013. |
| Yu ZB, Liu D, Lu HS, et al., 2012. A multi-layer soil moisture data assimilation using support vector machines and ensemble particle filter. Journal of Hydrology, 475:53-64. DOI:10.1016/j.jhydrol.2012.08.034. |
 2016, 8
2016, 8


