Article Information
- AiPing Tang, AnPing Zhao, AiHua Wen. 2015.
- Vibration characteristics of frozen soil under moving track loads
- Sciences in Cold and Arid Regions, 7(4): 414-420
- http://dx.doi.org/10.3724/SP.J.1226.2015.00414
Article History
- Received: February 26, 2015
- Accepted: May 18, 2015
2. School of Civil Engineering, Heilongjiang University, Harbin, Heilongjiang 150080, China;
3. China Academy of Architecture and Building, Beijing 100035, China;
4. School of Science, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
1 Introduction
The rapidly developing track transportation system in the frozen regions of northern and western China has brought not only environmental problems, but also damage risk to frozen soils, particularly in permafrost. Frozen soil damage has become an important issue affecting traffic safety and its sustainable development in cold regions. Generally speaking, frozen soil subsidence and large deformations are typical hazards due to track vibration loads, especially for express track systems. Soil vibration characteristics and responses arefundamental problems in soil deformation and subsidence mechanisms trigged by traffic vibration. Although research on traffic vibration mechanism and its action on soil and structure have a long history, very few studies involve soil dynamic response of movingtraffic loads under railways(Sheng et al., 1999; Hall, 2003; Takemiya, 2003;Zhang, 2007). In order to explore the vibration characteristics of frozen soil and assess the potential hazard due to moving track load, the seismic observation array technique(SOA) and finite element analysis(FEA)are presented in this paper to provide vibration signals and simulate frozen soil dynamic response under moving traffic load. Based on SOA and FEA, the relationship betweensoil dynamic characteristic with traffic vibration frequency and moving velocity was analyzed. The vibration attenuation characteristics was also studied, which may be helpful for foundation design to resist traffic vibration damage and environmental protection in cold regions, particularly for the rapidly developing railway system in Qinghai Province, Tibet and Northern Heilongjiang Province.
2 Vibration characteristics based on seismic observation arraySeismic observation array technology(SOA)is a common tool in monitoring seismic waves and its propagation during earthquakes or micro tremors. In general, SOA consists of at least five sets of seismographs, installed according to signal capturing requirements. In this paper, a linear and rectangular SOA were set up to monitor vibration signals of frozen soil along the Daqing-Harbin Railway line, perpendicular and parallel to the track line, respectively(Figure 1). The linear array was used to study the relationship of vibration characteristics at a remote distance from the track line. The rectangular array was applied to explore the vibration field of frozen soil when the train entered and exited the array. Typical vibration signals are presented in Figures 2a, b. According to field observation tests, one can get a sense of how vibration characteristics and it spatial distribution in frozen soils operate.
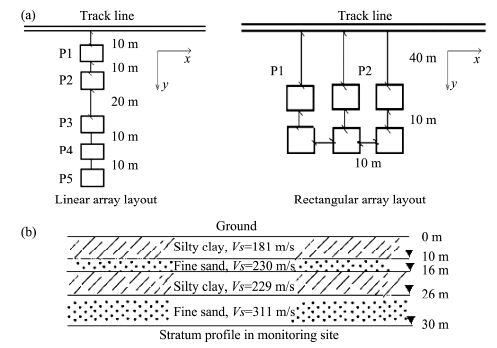 |
| Figure 1 Layout of SOA for vibration monitoring(a) and site stratum profile(b) |
Based on acceleration power spectrum analysis, the vibration frequency changes from 10 to 80 Hz, the predominant frequency is 15-60 Hz(Figure 2c), herein, the frozen soil temperature is −2 °C, and train velocity is about 60 km/h. In linear SOA, vibration characteristics are different in space, not only the amplitude, but also wave form, and the vibration has an obvious attenuation with increasing distance from the track line(Figure 2a). Based on the 20 time-history in the linear array, the maximum acceleration amplitudes in the three directions have obvious attenuation tendency(Table 1). However along the track line or perpendicular to track line, from track line to 20 m, the acceleration attenuation in the vertical direction is more rapid decreasing than that in the horizontal surface. From 20 to 50 m, the acceleration has a similar propagation attenuation rate, but from 50 to 60 m, the acceleration has a small increasing and the attenuation is much slower. The predominant frequency is 54 Hz(P1), 34 Hz(P2), 46 Hz(P3), 26 Hz(P4) and 22 Hz(P5), respectively. Thus, the number of high frequency vibrations increases closer to the track line. The SOA test has also detected that the weight of train has effect on the vibration due to the running track, including the acceleration and frequency of vibration in vertical and horizontal directions(Figure 3). Overall, train velocity, frozen soil temperature and water content, and stratum structure of the soil have a dramatic effect on vibration characteristics.
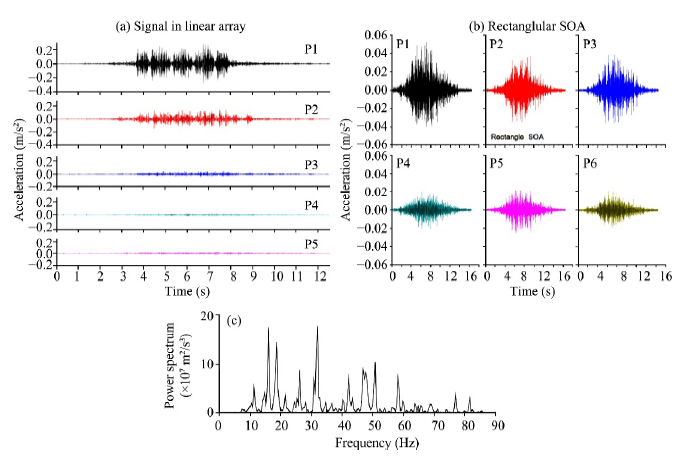 |
| Figure 2 Typical vibration histories in SOA.(a)acceleration history in linear array;(b)acceleration histroty in rectangular array;(c)typical power spectrum characteristics |
| Distance from the track line(m) | z(vertical direction; m/s2) | x(parallel to track line in horizon surface; m/s2) | y(perpendicular to track line in horizon surface; m/s2) |
| 10 | 0.2168 | 0.1071 | 0.0894 |
| 20 | 0.1400 | 0.0972 | 0.0749 |
| 40 | 0.0500 | 0.0300 | 0.0303 |
| 50 | 0.0262 | 0.0195 | 0.0180 |
| 60 | 0.0299 | 0.0241 | 0.0258 |
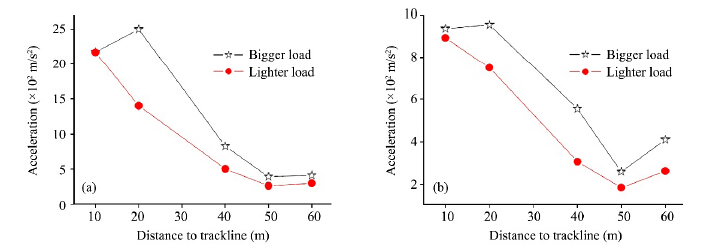 |
| Figure 3 The relationship between train weight and acceleration amplitudes.(a)relationship of vertical acceleration in vertical direction, load and distance to trackline;(b)relationship of vertical acceleration in direction of perpendicular to trackline, load and distance to trackline |
Based on 50 observation tests and 813 records, considering train velocity, unevenness of track and foundation, bump of the train, wheel weight, and referring to models of Volberg(1983), Pan(1994), and Yoshioka(2000), the train vibration load model can beconstructed:
| $\begin{array}{l} F(t) = {k_1}{k_2}{F_0}(t)\\ = {k_1}{k_2}({P_0} + {P_1}\sin {\omega _1}t + {P_2}\sin {\omega _2}t + {P_3}\sin {\omega _3}t) \end{array}$ | (1) |
| ${P_i} = {M_0}{a_i}\omega _i^2$ | (2) |
| ${\omega _i} = 2{\rm{\pi }}v/{L_i}$ | (3) |
There are numerous studies that explored the dynamic response mechanism of soil under track loads. Volberg(1983) and the Japan Railway Technique Institute(Yoshioka, 2000)provided several formulations for non-frozen soil dynamic characteristics under train-induced ground vibration. Hall(2003)studied a method based on two- and three-dimensional calculations to analyze train-induced ground vibration. Hanazato et al.(1991)analyzed traffic-induced ground vibrations based on a 3D simulation. Krylov(1997)analyzed the spectra of low-frequency ground vibrations generated by high-speed trains on layered ground. Takemiya(1997)studied a formula for predicting ground vibration induced by high-speed train operation. Volberg(1983)studied the propagation characteristics of ground vibration near railway tracks. Xia et al.(2005)performed numerous experiments to study train-induced vibrations on the environment and nearby buildings. These studies have shown that soil vibration induced by moving track load was is mainly related to soil characteristics, train velocity and train weight etc.. To simulate the dynamic response of frozen soil, train velocity and its vibration frequency, temperatures were selected herein and a numerical analysis was performed based on the ABAQUS platform. The soil parameters are listed in Table 2, and the Mohr-Coulomb model was selected to describe the stress-strain relationship. The boundary was simulated by a viscos-elastic element.
| Soil classification | Temperature(°C) | Density(kg/m3) | Elastic modulus, E(MPa) | Poisson's ratio, υ | C(MPa) | Friction angle(°) |
| Foundation filling soil | −5 −7 −10 −12 >0 | 2, 000 | 200.39 | 0.32 | 0.50 | 18.75 |
| 231.13 | 0.30 | 0.70 | 20.25 | |||
| 271.94 | 0.28 | 1.00 | 22.50 | |||
| 296.32 | 0.27 | 1.20 | 24.00 | |||
| 61.00 | 0.35 | 0.03 | 15.00 | |||
| Silt clay | −5 −7 −10 −12 >0 | 1, 920 | 99.01 114.67 135.46 147.88 28.00 | 0.36 0.34 0.32 0.30 0.40 | 0.60 0.80 1.00 1.20 0.15 | 17.00 18.20 20.00 21.20 14.00 |
| Strong weathered rock | −5 −7 −10 −12 >0 | 2, 000 | 424.04 486.68 569.84 619.52 140.00 | 0.23 0.22 0.21 0.20 0.25 | 1.30 1.80 2.50 3.00 0.10 | 24.50 26.30 29.00 30.80 20.00 |
| Source: Li et al., 2008; Gu, 2009. | ||||||
The model based on ABAQUS is listed in Figure 4. Here, x is parallel to the track line, z is the vertical direction perpendicular to the surface, and y is the direction perpendicular to the track line in the horizon.
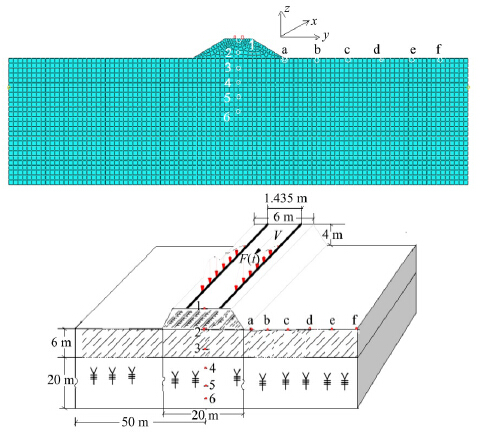 |
| Figure 4 Model based on ABAQUS for simulating the dynamic response of frozen soil under track loads.(a)a FEA model for simulating dynamic response of the subgrade soil under moving track load;(b)subgrade soil profile, foundation and moving track load |
Numbers 1-6 are points below the sleeper with the distance from the surface of 0, 4, 8, 12, 16, 20 m, letters a-f are points along the surface perpendicular to and at a distance away from the sleeper of 5, 10, 20, 30, 40 m, train velocity is 40, 60, 80, 100, 120 km/h, temperature fields of subgrade and foundation is 0, −5, −7, −10, −12 °C, respectively. The acceleration time history in vertical and horizontal directions was calculated and the results are illustrated in Figure 5(temperature is −5 °C).
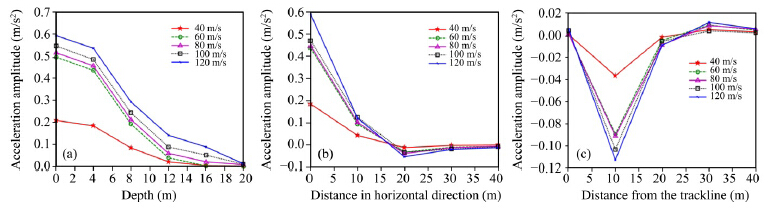 |
| Figure 5 Acceleration attenuation of different velocities in relation to depth and horizontal distance from the track line(temperature is −5 °C).(a)relationship of vertical acceleration in z-direction and train velocity in different depth;(b)relationship of vertical acceleration in y-direction and train velocity in horizontal direction;(c)relationship of horizontal acceleration in y-direction and train velocity in horizontal direction |
According to our simulation, the distinct vertical acceleration response in the z direction is strongly related to train velocity. However, for depth, vertical acceleration has a rapid attenuation, and was propagated only about 20 m. For horizontal direction, the attenuation of vertical acceleration and horizontal acceleration in the y direction was also rapid within 20 m, but their propagation lasted until 40 m distance from the track line. The frozen soil temperature is also a key factor which affects the dynamic response of frozen soils. Dynamic response of five frozen soils with temperatures of 0, −5, −7, −10, −12 °C were analyzed of which are illustrated in Figure 6(train velocity is 60 km/h).
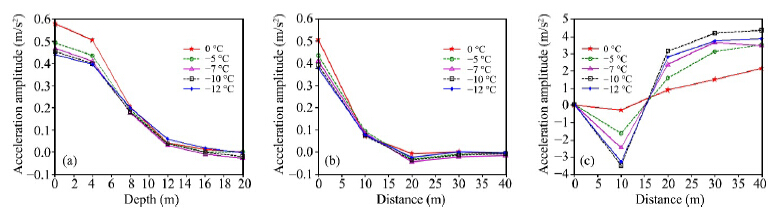 |
| Figure 6 Relationship on acceleration attenuation of different frozen soils and depth and horizontal distance from the track line.(a)relationship of vertical acceleration in z-direction and frozen soil temperuture in different depth;(b)relationship of vertical acceleration in y-direction and frozen soil temperuture in different distance;(c)relationship of horizontal acceleration in y-direction and frozen soil temperuture in different distance |
These results show an obvious temperature relationship on dynamic response of frozen soil in a limited spatial range. For horizontal direction, vertical acceleration within only 10 m had a strong relation to frozen temperature, but horizontal acceleration was more dependent on temperature. For depth, the more shallow the depth, the larger the vertical acceleration within 8 m, however the temperature changed. Over 8 m, the temperature had minimal effect on the dynamic response of frozen soil.
For train vibration source frequency relationship on dynamic response of soil and frozen soil, some studies have provided valuable conclusions that this source frequency had a great effect on the soil dynamic response(Cui, 2009; Gu, 2009; Zhu, 2009; Wang, 2011; Wei, 2011). This paper analyzed the dynamic response of frozen soil under train vibration source with different frequencies based on the aforementioned conclusions, inversion of SOA experiment, and in-situ test. Because the train vibration source frequency varied with the change of unevenness characteristics of track and foundation, the frozen soil temperature, train velocity and weight, and track-sleeper-subgrade structure, the range of vibration source frequency was widely distributed. Compared with non-frozen soil, the range of vibration source frequency in frozen soil was relatively narrow, its main frequency was 40-80 Hz when the frozen soil temperature was below −3 °C and −5 °C, the lower the temperature, the higher the frequency, and nearly 80% energy was concentered in 60-80 Hz(Figure 7). The natural frequency of subgrade was 30-50 Hz in winter and 30-40 Hz in summer, respectively(Figure 8). Thus, the dynamic response of frozen soil in winter is smaller than in summer, because the resonance of train vibration source and subgrade is easily transmitted in summer.
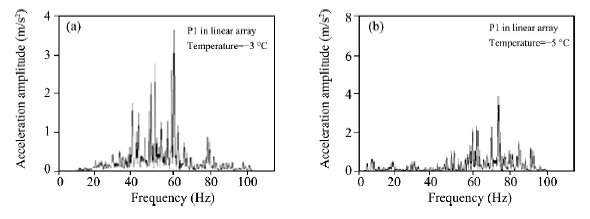 |
| Figure 7 Acceleration Fourier spectra amplitude in different soil tempratures.(a)vibration source predominant frequency in −3 °C frozen soil;(b)vibration source predominant frequency in −5 °C frozen soil |
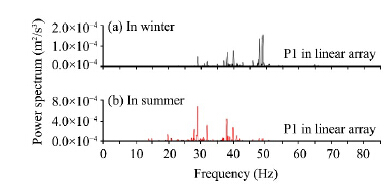 |
| Figure 8 Power Fourier spectra in summer and winter |
Vibration response characteristics of frozen soil under moving train loads was analyzed in this paper. The vibration signal in a frozen soil field can be successfully captured by use of the seismic observation array(SOA), which is a powerful tool in exploring the vibration of frozen soil. Based on SOA, a train vibration load model was constructed, considering train velocity, unevenness of track and foundation, bump of the train, and wheel weight.
The numerical simulation aimed at the parameter analysis for controlling the dynamic response characteristics of frozen soil. Our simulation shows that the vertical acceleration amplitude is the main vibration component and has the main energy, which means that vertical acceleration is the main factor for frozen soil damage. The train velocity, train vibration source frequency and temperature of frozen soil are three important factors that control the dynamic response of frozen soil under moving track loads, but only in a limited spatial range with an obvious temperature relationship on dynamic response of frozen soil.
Acknowledgments: This research is supported by the National High Technology Research and Development Program of China(863, 2008AA11Z104). Many thanks for colleague comments on this manuscript, kind and careful jobs from the editors of this journal, which make this paper perfect.| Cui GH, 2009. On environmental vibration induced by urban rail transit and virtual inversion for track irregularity spectrum's parameters. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China. |
| Gu HD, 2009. Numerical analysis of frozen soil foundation under traffic dynamic loads. Master Thesis of Harbin Institute of Technology, Harbin,China. |
| Hall L, 2003. Simulations and analyses of train-induced ground vibrations in finite element models. Journal of Soil Dynamics and Earthquake Engineering, 23(5): 403-413.DOI:10.1016/S0267-7261(02)00209-9. |
| Hanazato T, Ugai K, Mori M, et al.,1991. Three-dimensional analysis of traffic-induced ground vibrations. Journal of Geotechnical Engineering, ASCE, 117(8): 1133-1151.DOI: http://dx.doi.org/10.1061/(ASCE)0733-9410(1991)117:8(1133). |
| Krylov VV, 1997. Spectra of low-frequency ground vibrationsgenerated by high-speed trains on layered ground. Journal ofLow Frequency Noise, Vibration and Active Control, 16(4): 286-290. |
| Li SY, Zhang MY, Zhang SJ, et al., 2008. Analysis of the dynamic response of Qinghai-Tibetan railway embankment in permafrost regions under train load. Journal of Glaciology and Geocryology, 30(5): 860-867. |
| Pan CS, 1994. A FEA of dynamic response for tunnel in Yellow soil. Journal of Civil Engineering, 17(4): 19-28. |
| Sheng X, Jones CJC, Petyt M, 1999. Ground vibration generated by a load moving along a railway track. Journal of Sound and Vibration, 228(1): 129-156. DOI: 10.1006/jsvi.1999.2406. |
| Takemiya H, 1997. Prediction of ground vibration induced by high-speed train operation. In: 18th Sino-Japan Technology Seminar, Taipei, Taiwan. |
| Takemiya H,2003.Simulation of track-ground vibrations due to a high-speed train: the case of X-2000 at Ledsgard. Journal of Sound and Vibration, 261(3): 503-526.DOI: 10.1016/S0022-460X(02)01007-6. |
| Volberg G, 1983. Propagation of ground vibration near railway tracks. Journal of Sound and Vibration, 87(2): 371-376. DOI: 10.1016/0022-460X(83)90576-X. |
| Wang FT, 2011. Inversion of ground vibration source by urban railway traffic in frequency domain. Ph.D. Dissertation of Harbin Institute of Technology, Harbin, China. |
| Wei H, 2011. Study on near-field barrier isolation of train-induced vibration in frozen field. Master thesis of Harbin Institute of Technology, Harbin, China. |
| Xia H, Zhang N,Cao YM, 2005. Experimental study of train-induced vibrations of environments and nearby buildings. Journal of Sound and Vibration, 280(3-5): 1017-1029. DOI: 10.1016/j.jsv.2004.01.006. |
| Yoshioka G, 2000. Basic Characteristics of Shinkansen-induced Ground Vibration and Its Reduction Measures.Bochum, Germany:Proceeding of WAVE 2000International Workshop: Wave Propagation,Moving load,Vibration Reduction, BalkemaPublishers,pp. 219-239. |
| Zhang JQ, 2007. Simulation of soil dynamic response under moveable track traffic loads. Master Thesis of Harbin Institute of Technology, Harbin, China. |
| Zhu ZY, 2009. Train-induced vibration response and subsidence prediction of permafrost subgrade along Qinghai-Tibet railway. Ph.D. Dissertation of Harbin Institute of Technology, Harbin,China. |
 2015, 7
2015, 7


