Article Information
- XiaoLiang Yao, MengXin Liu, Fan Yu, JiLin Qi. 2015.
- Evaluation of creep models for frozen soils
- Sciences in Cold and Arid Regions, 7(4): 392-398
- http://dx.doi.org/10.3724/SP.J.1226.2015.00392
Article History
- Received: February 10, 2015
- Accepted: April 16, 2015
2. School of Civil and Transportation Engineering, Beijing University of Architecture and Civil Engineering, Beijing 100044, China
1 Introduction
In the past decades, large scale permafrost degradation has been observed due to global warming and increased infrastructure activities in cold regions. With the degradation of permafrost, successive and large creep settlement of foundations have often been observed(Tsytovich, 1975; Qi et al.,2007). To get a better underst and ing of the creep behavior of frozen soils, a lot of experimental work has been carried out since the 1980s(Ladanyi, 1983; Zhu and Carbee, 1983; Vyalov, 1986). It was shown that, with increase of time three stages can be defined as primary, secondary and tertiary stages(Ladanyi, 1972; Zhu and Carbee, 1983). Based on this, some empirical fitting equations taking account of the effect of stress level, ice content and temperature were proposed(Vyalov, 1962; Goughnour and Andersl and , 1968; Ting and Martin, 1979; Assur, 1980; Ting, 1983). The experimental studies provide a great help in underst and ing the complicated creep behaviors of frozen soils, but cannot be extended to problems with more complicated conditions.
To describe the creep behaviors of frozen soils in more general stress and strain states, theoretical models are often employed. As far as the authors know, three kinds of models can be classified. The first is the microscopic model, which incorporates thermodynamics and damage mechanics to reflect microscopic changes during creep of the geomaterials(Miao et al.,1995; He et al.,1999). These models reasonably describe the creep mechanism from the microscopic point of view. However, the variables in these models are difficult to determine in the laboratory which restrains their application in engineering. The second is the theory of hypoplasticity. Since the 1980s, this theory has been derived from the theory of thermodynamics to model the stress-strain relationships of geomaterials(Dafalias, 1986; Wu and Kolymbas, 1990; Wu and Niemunis, 1996). In this theory, without the hypothesis of plastic potential, plastic flow rule, hardening rule and yield surface, the simple mathematical relationship between stress rate and strain rate were given directly. Based on this, Xu(2014)further developed a hypoplasctic creep model for frozen soil, with which, the stress-strain relationships can be well described when large plastic deformation of soil occurs. The third is so called elastic-visco-plastic model, which is widely used in conventional soil mechanics. Due to the advantage of clear physical meaning and numerical convenience of conventional elemental rheological models, researchers developed different kinds of creep models for frozen soil by incorporating the yield criteria, hardening, plastic flow rules and long term strength of frozen soils(Yang et al.,2010; Li et al.,2011; Wang et al.,2014). Besides the elementary rheological models, a kind of soft soil creep model has recently been well developed(Kutter and Sathialingam, 1992; Den Haan, 1996; Vermeer and Neher, 1999). This model is based on the isotache and modified Cam-Clay models, and shows a good linear relationship between strain and time in semilog coordinates(Buisman, 1936; Bjerrum, 1967; Garlanger, 1972). According to the test results of frozen soil(Ma et al.,1994; Wu and Ma, 1994), the development of creep strain obeys the same law as well. Furthermore, all the parameters required in the soft soil creep model can be obtained directly from conventional tests, which makes it easier to apply this model to frozen soil. As mentioned, there are three models(i.e., hypoplastic creep, elementary rheological and soft soil creep)that can be conveniently applied in frozen soil engineering problems. However, due to lack of evaluation on the applicability of each model, engineers are not certain about the model selection according to engineering conditions. It is therefore important to evaluate these models.
In this paper, the prediction accuracy of three models(elementary rheological, soft soil creep and hypoplastic creep)is examined by comparing a series of uniaxial shear test results. Other factors affecting the prediction accuracy of the three models are also analyzed. Based on these results, the conditions for applicability of each model are estimated.
2 Creep models descriptionsIn the following all stresses refer to effective stresses.
2.1 Hypoplastic creep modelFollowing the framework of Wu and Kolymbas(1990), Xu(2014)proposed a creep model for frozen soils as follows
| $\begin{array}{l} {{\dot \sigma }_{ij}} = {c_1}[tr({\sigma _{ij}} - s)]{{\dot \varepsilon }_{ij}} + {c_2}\frac{{tr[({\sigma _{ij}} - s){{\dot \varepsilon }_{ij}}]}}{{tr({\sigma _{ij}} - s)}}({\sigma _{ij}} - s) + \\ \quad \quad f({{\dot \varepsilon }_{ij}})\left[ {{c_3}{{({\sigma _{ij}} - s)}^2} + {c_4}({\sigma _{ij}} - s)_d^2} \right] \end{array}$ | (1) |
| ${({\sigma _{ij}} - s)_d} = ({\sigma _{ij}} - s) - \frac{1}{3}(tr({\sigma _{ij}} - s)){\delta _{ij}}$ | (2) |
In Equation (1), $f({\dot \varepsilon _{ij}})$ is a scalar function regarding deformation, which can be expressed as
| $\lg [f({\dot \varepsilon _{ij}})] = {c_5}[\lg (l) + {c_6}] + \frac{{{c_7}}}{{\lg (l) + {c_6}}} + {c_8}$ | (3) |
Due to the clear physical meaning and numerical convenience in programing, the elementary rheological models were used to describe the 1-D creep behaviors of frozen soils(Vyalov, 1986; Li et al.,2011). Based on the hypothesis of the effect of spherical and deviatoric stresses, some models were proposed to predict the creep behavior in 3-D conditions(Yang et al.,2010; Wang et al.,2014). Here, a frozen soil elementary rheological model with parabolic yield criterion is expressed as follows(Wang et al.,2014),
| $\left\{ \begin{array}{l} {\varepsilon _{ij}} = \frac{{{\sigma _{ij}}}}{{2{G_M}}} + \frac{{{\sigma _{ij}}}}{{2{H_M}}}t + \\ \frac{{{\sigma _{ij}}}}{{2{G_K}}}\left[ {1 - {\rm{exp}}\left( { - \frac{{{G_K}}}{{{H_K}}}t} \right)} \right]\left( {\phi {\rm{(}}F{\rm{)}} \le 0} \right)\\ {\varepsilon _{ij}} = \frac{{{\sigma _{ij}}}}{{2{G_M}}} + \frac{{{\sigma _{ij}}}}{{2{H_M}}}t + \frac{{{\sigma _{ij}}}}{{2{G_K}}}\left[ {1 - {\rm{exp}}\left( { - \frac{{{G_K}}}{{{H_K}}}t} \right)} \right]\\ + \frac{1}{{2{H_N}}}\left\langle {\phi \left( F \right)} \right\rangle \frac{{\partial Q}}{{\partial \left\{ \sigma \right\}}}t\left( {\phi {\rm{(}}F{\rm{)}} > 0} \right) \end{array} \right.$ | (4) |
| $\phi (F) = \left\langle {\frac{F}{{{F_0}}}} \right\rangle $ | (5) |
| $F = \sqrt {3{J_2}} - s - {\sigma _m}\tan \varphi + \frac{{\tan \varphi }}{{2{p_m}}}\sigma _m^2$ | (6) |
In this model the rheological parameters, i.e., GK, GM, HK, HM and HN can be fitted by the least square method while the strength parameters, i.e., s, φ and pm are obtained from the shear test results on the same material.
2.3 Soft soil creep modelBefore discussing the 3D soft soil creep model, it is better to introduce the conception of 1D isotache model(Den Haan, 1996)which is the basis of the 3D model. In this isotache model, the total strain is obtained by adding the elastic strain(εe) and viscoplastic strain(εvp), i.e.,
| ${\varepsilon _e} = a\ln (\frac{\sigma }{{{\sigma _0}}})$ | (7) |
| ${\varepsilon _{vp}} = b\ln (\frac{\sigma }{{{\sigma _p}}}) + c\ln (\frac{\tau }{{{\tau _p}}})$ | (8) |
| ${\dot \varepsilon _e} = a\frac{{\dot \sigma }}{\sigma }$ | (9) |
| ${\dot \varepsilon _c} = \frac{c}{\tau }$ | (10) |
Subtract Equation (7) from (8) at σ0=σp and substitute Equation (10) into (8), the creep strain rate can be written as
| ${\dot \varepsilon _c} = \frac{c}{{{\tau _1}}}{e^{ - {\varepsilon _c}/c}}{(\frac{\sigma }{{{\sigma _p}}})^{(b - a)/c}}$ | (11) |
Equation (11) can further be expressed as
| ${\dot \varepsilon _c} = \frac{c}{{{\tau _1}}}{(\frac{\sigma }{{{\sigma _c}}})^{(b - a){\rm{/}}c}}$ | (12) |
| ${\sigma _c} = {\sigma _p}{e^{{\varepsilon _c}/(b - a)}}$ | (13) |
To extend the 1D model to general states of stress and strain, Equations (12) and (13) can be written as
| ${\dot \varepsilon _{cv}} = \frac{c}{{{\tau _1}}}{(\frac{{{p_{eq}}}}{{{p_c}}})^{(b - \alpha ){\rm{/}}c}}$ | (14) |
| ${p_c} = {p_0}{e^{{\varepsilon _{cv}}/(b - \alpha )}}$ | (15) |
| $\left\{ \begin{array}{l} {p_{eq}} = p + \frac{{{q^2}}}{{{M^2}p}}\\ p = \frac{1}{3}({\sigma _{11}} + {\sigma _{22}} + {\sigma _{33}})\\ q = \frac{1}{{\sqrt 2 }}\sqrt {{{({\sigma _{11}} - {\sigma _{22}})}^2} + {{({\sigma _{11}} - {\sigma _{33}})}^2} + {{({\sigma _{22}} - {\sigma _{33}})}^2}} \end{array} \right.$ | (16) |
| $M = \frac{{6\sin \varphi }}{{3 - \sin \varphi }}$ | (17) |
Equation (16) was proposed for cohesionless material. In the presence of cohesion, p can be replaced with p' as
| $\left\{ \begin{array}{l} p' = p + \cot (\varphi )s\\ p = \frac{1}{3}({\sigma _{11}} + {\sigma _{22}} + {\sigma _{33}}) \end{array} \right.$ | (18) |
To obtain the creep strain rate in a general stress state, an associated flow rule is employed as
| ${\left( {{{\dot \varepsilon }_c}} \right)_{ij}} = \lambda \frac{{\partial {p_{eq}}}}{{\partial {\sigma _{ij}}}}$ | (19) |
in which peq is taken as plastic potential function. According to Equation (19), εcv can be further expressed as
| ${\dot \varepsilon _{cv}} = \lambda (\frac{{\partial {p_{eq}}}}{{\partial {\sigma _{11}}}} + \frac{{\partial {p_{eq}}}}{{\partial {\sigma _{22}}}} + \frac{{\partial {p_{eq}}}}{{\partial {\sigma _{33}}}})$ | (20) |
Substitute Equations (14) and (20) into (19), Equation (19) can be rewritten as
| ${\left( {{{\dot \varepsilon }_c}} \right)_{ij}} = \frac{c}{{{\tau _1}}}{(\frac{{{p_{eq}}}}{{{p_c}}})^{(b - \alpha )/c}}\frac{{\partial {p_{eq}}}}{{\partial {\sigma _{ij}}}}$ | (21) |
With Equation (21), the creep strain rate in a general stress state can be calculated.
3 Calculating results and analysisA series of uniaxial compression(σ22=σ33=0)creep tests results on frozen Karlsruhe medium s and conducted by Orth(1986)are used here to verify the applicability of the three models. The prepared samples have a dry unit weight of 17.2 kN/m3 and water content of 18%. In these tests, axial stresses(σ11)range from 1 to 10 MPa and the testing temperature is −10 °C. According to Sections 2.1-2.3, the parameters needed for each models are listed in Tables 1-3.
| s(kPa) | c1 | c2 | c3(kPa−1·s−1) | c4(kPa−1·s−1) | c5(kPa) | c6(kPa) | c7(kPa) | c8(kPa) |
| 3, 061.9 | −68.82 | −673.56 | 0.0768 | −0.0256 | 0.066σ1−1.076 | 0.034σ1−0.462 | 0.652σ1−14.520 | 0.522σ1−8.883 |
| GM(MPa) | GK(MPa) | HK(MPa·h) | HM(MPa·h) | HN(MPa·h) | S(MPa) | φ(°) | pm(MPa) |
| 52.8 | 60.0 | 200 | 1, 246 | 15 | 3.06 | 30.1 | 10.1 |
| a | b | c | τ1(min) | p0(kPa) | S(MPa) | φ(°) | v |
| 0.0001 | 0.0018 | 0.0019 | 120 | 350 | 3.06 | 30.1 | 0.3 |
Figures 1-3 are the calculated and tested results of axial strain and strain rate versus time at different stress levels. It can be seen from the test results that, for lower stress levels(σ11 <6 MPa), the primary creep stage can be observed, and the strain rate decreases continuously. For the higher stress levels(σ11 ≥6 MPa), all three creep stages can be observed, and developing of strain rate shows a tendency of decreasing at first, then essentially remains constant and finally increases. Comparing the test results and calculated results, it is clear that the hypoplastic creep model shows good agreement with the test results with both the creep strain and strain rate at different stress levels. As far as the three creep stages are concerned, there is a structural deterioration and localized damage developing(Assur, 1980; Ting, 1983; Zhu and Carbee, 1983). Considering the effect of structural deterioration on creep deformation, two terms of the deformation function are employed to describe the creep strain at different stages(Equation (3)). In this way, it can be seen that the conversion process between different creep stages can be simulated as smoothly as the tested results(Figure 1). It can be said that this model is applicable in engineering problems with a wide range of mechanical conditions.
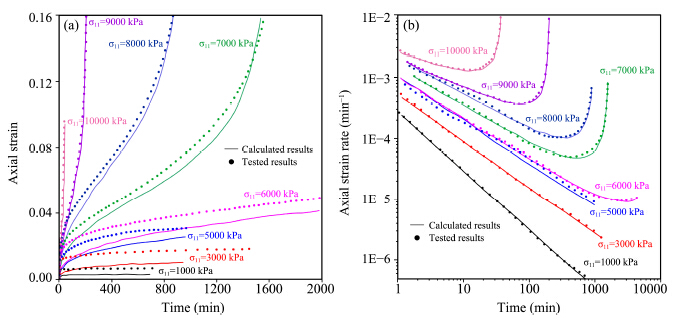 |
| Figure 1 Changes in axial strain(a) and strain rate(b)versus time(Hypoplastic creep model) |
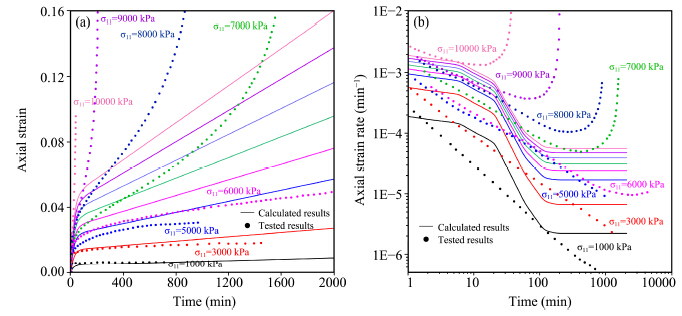 |
| Figure 2 Changes in axial strain(a) and strain rate(b)versus time(Elementary rheological creep model) |
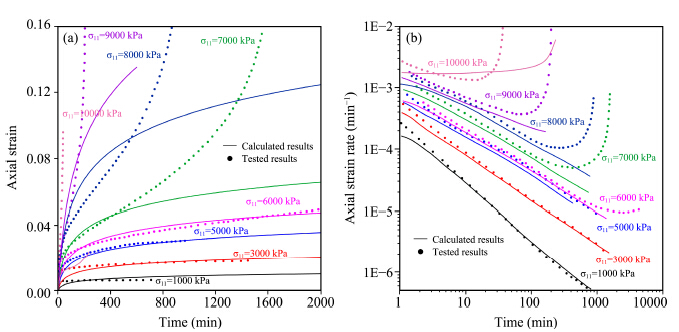 |
| Figure 3 Changes in axial strain(a) and strain rate(b)versus time(Soft soil creep model) |
For the elementary rheological creep model, it can be seen that the calculated results match well with the test results at low stress levels of the creep strain(Figure 2). For the strain rate, the calculated results show a totally different change tendency with the test results, i.e., strain rate decreases nonlinearly at first and then essentially remains constant. The tertiary creep stage cannot be captured by this model, which is caused by the mathematical construction of this model. With the Maxwell and Kelvin terms(Equation (4)), the decrease and constant creep stages of strain rate can be simulated. For the third stage, the Bingham term with the parabolic yield criterion(Equation (4))is used to calculate plastic strain. Obviously, this term is linearly correlated with time and cannot reflect the nonlinear increase of strain rate when shear failure occurs. It can be concluded that this model can only be used for the development of creep strain at low stress levels. It has a low accuracy for the simulating of strain rate.
As for the soft soil creep model(Figure 3), it can be seen that this model shows a fairly good prediction accuracy at low stress levels(1-6 MPa)in both creep strain and strain rate. For the higher stress levels(>6 MPa), the simulation accuracy decreases with the increase of stress level. Below 9 MPa, the calculated results on both of creep strain and strain rate show similar changes, i.e., the strain rate decreases continuously. It is a strain hardening process. Once the stress level is larger than 9 MPa, only an increase in the calculated strain rate can be observed. Obviously, with the soft soil creep model, the progressive development from primary to secondary and tertiary stages cannot be captured. The soft soil creep model is deduced from modified Cam-Clay model, which was originally developed for the strain hardening and shear failure behavior for unfrozen soils. For frozen soils, the change from second to tertiary stages is actually induced by the structural deterioration with time(Assur, 1980; Ting, 1983; Zhu and Carbee, 1983). Therefore, to describe the three creep stages reasonably, this feature of frozen soil should be taken into consideration. However, considering the accuracy at low stress levels, the soft soil creep model still can be used when the tertiary stage is not involved.
4 ConclusionsIn this paper, the prediction performance of three creep models was examined using a series of uniaxial creep tests at different stress levels. The applicability of each model was analyzed. The following can be concluded:
1)Three creep stages can be observed at high stress levels caused by the development of frozen soil structural deterioration and localized damage. This should be taken into consideration to describe the three creep stages comprehensively.
2)The hypoplastic creep model can describe the three creep stages reasonably and can be used in engineering problems with a wide range of mechanical conditions. By incorporating a deformation scalar function, the effects of structural deterioration and localized damage on creep deformation can be well captured.
3)The elementary rheological creep model can only be used for the predicting of creep strain at low stress levels. It has a low accuracy for the strain rate which is due to the restraint of its mathematical construction.
4)The soft soil creep models cannot capture the progressive development process from primary to secondary and tertiary stages. It is applicable at low stress levels with a high prediction accuracy on creep strain and strain rate.
Acknowledgments: This work was supported in part by the National Natural Science Foundation of China(No. 41201064 and No. 41172253) and the National Key Basic Research(973)Program of China(Grant No. 2012CB026106).| Assur A, 1980. Some promising trends in ice mechanics in Physics and Mechanics of ice. International Symposium, Copenhagen, Springer-Berlin. |
| Bjerrum L, 1967. Engineering geology of Norwegian normally consolidated marine clays as related to settlements of buildings. Geotechnique, 17(2): 81-118. DOI: 10.1680/geot.1967.17.2. 83. |
| Buisman AS, 1936. Results of long duration settlement tests. In: Proc. 1st Int. Conf. Soil Mech., Found. Engng, Cambridge, 1, pp. 103-107. |
| Dafalias YF, 1986. Bounding surface plasticity, I: Mathematical foundation and hypoplasticity. Engineering Mechanics, ASCE, 112(9): 966-987. DOI: http://dx.doi.org/10.1061/(ASCE)0733-9399(1986)112:9(966). |
| Den Haan EJ, 1996. A compression model for non-brittle soft clays and peat. Géotechnique, 1: 1-16. DOI: 10.1680/geot.1996. 46.1.1. |
| Fish AM, 1980. Kinetic nature of the long-term strength of frozen soils. In: Proc. 2nd Int. Symp. on Ground Freezing, Norwegian Institute of Technology, Trondheim, pp. 95-108. |
| Garlanger JE, 1972. The consolidation of soils exhibiting creep under constant effective stress. Geotechnique, 22(1): 71-78. DOI: 10.1680/geot.1972.22.1.71. |
| Goughnour RR, Andersland OB, 1968. Mechanical properties of a sand-ice system. ASCE Journal of Soil Mechanics and Foundation Division Proceedings, 94(SM 4): 923-950. |
| He P, Cheng GD, Zhu YL, 1999. Constitutive theories on viscoelastoplasticity and damage of frozen soil. Science of China (Ser. D), 42(1): 38-43. DOI: 10.1007/BF02878851. |
| Kutter BL, Sathialingam N, 1992. Elastic-viscoplastic modelling of the rate-dependent behaviour of clays. Geotechnique, 42(3): 427-442. DOI: 10.1680/geot.1992.42.3.427. |
| Ladanyi B, 1972. An engineering theory of creep of frozen soils. Canadian Geotechnical Journal, 9(1): 63-80. DOI: 10.1139/ t72-005. |
| Ladanyi B, 1983. Shallow foundations on frozen soil creep settlement. Journal of Geotechnical Engineering, 109(11): 1434-1448. DOI: 10.1061/(ASCE)0733-9410(1983)109:11 (1434). |
| Li DW, Fan JH, Wang RH, 2011. Research on visco-elastic-plastic creep model of artificial frozen soil under high confining pressures. Cold Regions Science and Technology, 65(2): 219-225. DOI: 10.1016/j.coldregions.2010.08.006. |
| Li GX, 2004. Advanced Soil Mechanics. Beijing: Tsinghua University Press. |
| Ma W, Wu ZW, Sheng Y, 1994. Strength and creep of frozen soil. Journal of Glaciology and Geocryology, 16(2): 113-118. |
| Miao TD, Wei XX, Zhang CQ, 1995. Creep of frozen soil by damage mechanics. Science of China (Series B), 25(3): 309-317. |
| Orth W, 1986. Gefrorener Sand als Werkstoff: Elementversuche und Materialmodell. Publication Series of the Institute of Soil Mechanics and Rock Mechanics, Karlsruhe University, No. 100. |
| Qi JL, Sheng Y, Zhang JM, et al., 2007. Settlement of embankments in permafrost regions in the Qinghai-Tibetan Plateau. Norwegian Journal of Geography, 61(2): 49-55. DOI: 10.1080/00291950701409249. |
| Ting JM, Martin RT, 1979. Application of the Andrade equation to creep data for ice and frozen soil. Cold Regions Science and Technology, 1(1): 29-36. DOI: 10.1016/0165-232X(79) 90016-8. |
| Ting JM, 1983. Tertiary creep model for frozen sands. Journal of Geotechnical and Geoenvironmental Engineering, 109(7): 932-945. DOI: 10.1061/(ASCE)0733-9410(1983)109:7(932). |
| Tsytovich NA, 1975. The Mechanics of Frozen Ground. McGraw-Hill, Scripta Book Company, Washington D.C.. |
| Vermeer PA, Neher HP, 1999. A soft soil model that accounts for creep. In: Proceedings of the international symposium 'Beyond 2000 in Computational Geotechnics', Amsterdam, pp. 249-261. |
| Vyalov SS, 1962. Strength and creeo of frozen soils and calculations in ice-soil retaining structures. USACRREL translation, pp. 76. |
| Vyalov SS, 1986. Rheological Fundamentals of Soil Mechanics. Elsevier, Amsterdam. |
| Wang SH, Qi JL, Yin ZY, et al., 2014. A simple rheological element based creep model for frozen soils. Cold Regions Science and Technology, 106-107: 47-54. DOI: 10.1016/j.coldregions. 2014.06.007. |
| Wu W, Kolymbas D, 1990. Numerical testing of the stability criterion for hypoplastic constitutive equations. Mechanics of Materials, 9(3): 245-253. DOI: 10.1016/0167-6636(90)90006-2. |
| Wu W, Niemunis A, 1996. Failure criterion, flow rule and dissipation function derived from hypoplasticity. Mechanics of Cohesive-Frictional Materials, 1(2): 145-163. DOI: 10.1002/(SICI) 1099-1484(199604)1:23.0.CO;2-9. |
| Wu ZW, Ma W, 1994. Strength and Creep of Frozen Soil. Lanzhou, China: Lanzhou University Press. |
| Xu GF, 2014. Hypoplastic constitutive models for frozen soil. University of Natural Resources and Life Sciences, Vienna, No. 30. |
| Yang YG, Lai YM, Chang XX, 2010. Experimental and theoretical studies on the creep behavior of warm ice-rich frozen sand. Cold Regions Science and Technology, 63(1-2): 61-67. DOI: 10.1016/j.coldregions.2010.04.011. |
| Zhu YL, Carbee DL, 1983. Creep behavior of frozen silt under constant uniaxial stress. In: Proc., 4th Int. Conf. Permafrost, Fairbanks, Alaska, pp.1507-1512. |
 2015, 7
2015, 7


