Article Information
- QingBo Bai, Xu Li, YaHu Tian. 2015.
- A method used to determine the upper thermal boundary of subgrade based on boundary layer theory
- Sciences in Cold and Arid Regions, 7(4): 384-391
- http://dx.doi.org/10.3724/SP.J.1226.2015.00384
Article History
- Received: February 26, 2015
- Accepted: May 15, 2015
2.Qinghai Research and Observation Base, Key Laboratory of Highway Construction & Maintenance Technology in Permafrost Regions, Ministry of Transport, Xining, Qinghai 810001, China
1 Introduction
The simulation of subgrade temperature field is the foundation of the thermal stability analysis of subgrade in permanent and seasonal permafrost regions. In the numerical simulation of long-term subgrade temperature fields, it is difficult to accurately simulate the daily fluctuations of solar radiation and atmosphere temperature. By long-term observation, Zhu(1988)put forward the "boundary layer theory" as the upper thermal boundary to calculate the subgrade temperature field. The boundary layer theory assumes that the effect of daily solarradiation and air temperature are negligible at the bottom of the boundary layer; thus, soil temperature at the bottom of the boundary layer is equal to the atmosphere temperature plus a temperature increment.
Based on the boundary layer theory, boundary layer thickness and temperature increment are two major parameters involved in the upper boundary of subgrade in the numerical simulation of long-term temperature fields. Based on theoretical derivation, Bai et al.(2015)set up the theoretical solution of the boundary layer thickness and summarized the factors affecting the temperature increment.
Based on the typical designs of highway or railway, this paper sketches the design formulae of boundary layer thickness and the empirical equation of temperature increment. First, the subgrade pavement structures of typical roads are summarized, such as highway and railroad. Second, the boundary layer thicknesses are calculated and listed. Third, the main factors impacting the temperature increment are collected. Lastly, a numerical simulation is performed for the temperature field of a Qinghai-Tibet Highway embankment. The results are further comparedwith monitored data in the field.
2 The boundary layer theory of thermal conduction problem in pavement 2.1 The boundary layer theory of thermal conduction problemThe boundary layer theory was first introduced in hydromechanics and used to describe that laminar flow will be present when water has a critical distance d from the boundary. A similar phenomenon is observed in the thermal conduction problem of subgrade where the daily variation of temperature at a certain depth beneath ground surface is negligible. Such phenomenon is first termed as the "boundary layer theory" by Zhu(1988). Soil strata can be divided into three layers from top to bottom: convection heat exchange, radiation heat transfer, and heat-conduction; the radiation heat transfer layer is called "the boundary layer"(Zhu, 1988). Yan(1984)indicated that the boundary layer thickness is soil depth without the daily effect of solar radiation and air temperature.
The soil temperature at the bottom of the boundary layer(du)could be described by the equation:
| $T(t) = {T_a} + {T_i} + {\varepsilon _d}\sin ({\omega _d}t + \varphi )$ | (1) |
At a certain depth(du), ed is ignored as a small amount, meaning that the soil temperature is irrespective to the daily effect of solar radiation and air temperature. Therefore, the soil temperature at a certain depth(du)could be regarded as the upper thermal boundary in the numerical simulation of a long-term subgrade temperature field, and the valueof ed is set to zero to simplify the upper thermal boundary. The phenomena of boundary layer in subgrade could be described in Figure 1; the daily temperature amplitude in deeper soil is smaller, and the soil temperature is higher than air temperature.
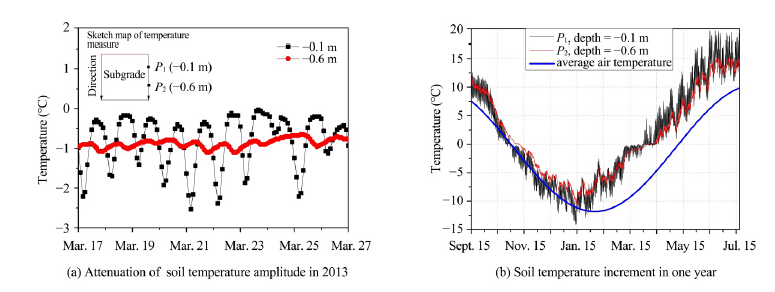 |
| Figure 1 Temperature of monitoring points |
Based on the boundary layer theory, boundary layer thickness(du) and temperature increment(Ti)are two major parameters in determining the upper thermal boundary.
2.2 Conversion parameters in the boundary layer theoryIn this paper, the criteria selecting boundary layer thickness is expressed with the equation:
| $\frac{{{\varepsilon _d}}}{{{A_s}}} \le 5\% $ | (2) |
The temperature amplitude in soil is smaller when the soil depth is larger. Bai et al.(2015)put forward the attenuation of temperature amplitude in m layers of soil which could be expressed with the equation:
| ${\upsilon _m} = \frac{{{A_s}}}{{{\varepsilon _d}}} = \exp (\xi ){\rm{ = }}\exp (\sum\nolimits_{i = 1}^m {{\xi _i}} )$ | (3) |
| ${\xi _i} = {\delta _i}\sqrt {\frac{{{\omega _d}}}{{2{\alpha _i}}}} $ | (4) |
| ${\alpha _i} = k/(C \cdot \rho )$ | (5) |
Based on Equation (4), xcould be expressed with the equation:
| $\xi = \sqrt {\frac{{{\omega _d}}}{{2\hat \alpha }}} \cdot \sum {{\delta _i} = \sum\nolimits_{i = 1}^m {{\delta _i}} } \sqrt {\frac{{{\omega _d}}}{{2{\alpha _i}}}} $ | (6) |
| $\hat \alpha = {(\frac{{\sum {{\delta _i}} }}{{\sum {({\delta _i}/\sqrt {{\alpha _i}} )} }})^2}$ | (7) |
The equivalent thermal diffusivity can reflect the attenuation degree of temperature amplitude through m layers of soil.
3 The calculation method and typical values of the boundary layer thickness 3.1 Theoretical solution of the boundary layer thicknessBased on the criteria of boundary layer thickness(Equation (4)), um is equal to 20 and xb is equal to 2.996. When the mth layer of soil in subgrade meets the conditions:
| $\sum\nolimits_{i = 1}^{m - 1} {{\xi _i}} {\rm{\& }}1t;{\xi _b}\;;\;\;\sum\nolimits_{i = 1}^m {{\xi _i} \ge {\xi _b}} $ | (8) |
The bottom of the boundary layer is in the mthlayer of soil and is hb distant from the top of the mth layer of soil. hb could be expressed in the equation:
| ${h_b} = ({\xi _b} - \sum\nolimits_{i = 1}^{m - 1} {{\xi _i}) \cdot \sqrt {\frac{{2{\alpha _m}}}{{{\omega _d}}}} } $ | (9) |
The boundary layer thickness($\delta _u $)could be expressed in the equation:
| ${\delta _u} = {h_b} + \sum\nolimits_{i = 1}^{m - 1} {{\delta _i}} $ | (10) |
Based on Equation (6), the boundary layer thickness corresponds to the equivalent thermal diffusivity. The numerical range of the equivalent thermal diffusivity of soil and cushion in subgrade is 2.5×10−7-1.05×10−6 m2/s(Xu et al., 2001); the numerical range of the equivalent thermal diffusivity of asphalt pavement is 4.3×10−7-8.7×10−7 m2/s(Lei, 2011;Zhang et al., 2011). Thus, the relationship between boundary layer thickness(du) and equivalent thermal diffusivity(α)could be expressed in Figure 2.
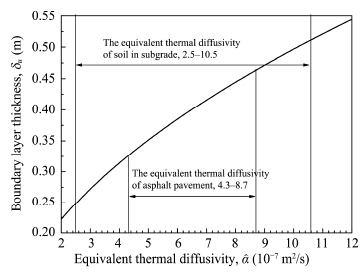 |
| Figure 2 Relationship between $\delta _u $ and $\hat \alpha $ |
The typical road includes highway and railroad; the highway pavement structure includes asphalt pavement and cement concrete pavement; the railroad pavement structure includes ballasted roadbed and ballastless roadbed. Based on the design codes and engineering practices(Wang, 2005; Zhang, 2012), four typical embankment structures are widely used in the construction of railway or highway in China, as illustrated in Figure 3. The equivalent thermal diffusivity and the boundary layer thickness of the embankment structures in typical roads is calculated and listed in Table 1.
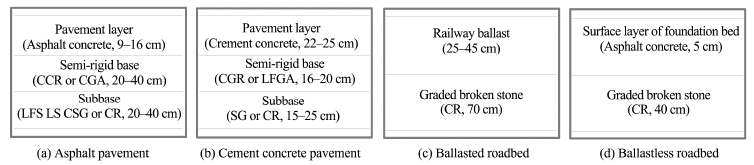 |
| Figure 3 Statistics of embankment structures |
| Pavement structure | Asphalt pavement | Cement concrete pavement | Ballasted roadbed | Ballastless roadbed |
| $\hat \alpha $(×10−7 m2/s) | 3.65-8.95 | 5.55-6.16 | 6.81 | 4.15-4.96 |
| $\delta _u $(m) | 0.30-0.47 | 0.37-0.39 | About 0.41 | 0.32-0.35 |
The temperature increment is relevant to the boundary thickness. Bai et al.(2015)put forward that the decisive factor of temperature increment is the effective solar radiation, and the influencing factors of temperature increment are heat-transfer coefficient(B) and equivalent thermal diffusivity($\hat \alpha $). The temperature increment could be designed with the following equation:
| ${T_i} = \lambda {Q_e}$ | (11) |
| $\lambda = {\eta _B}{\eta _\alpha }{\lambda _c}$ | (12) |
| $\left\{ {\begin{array}{*{20}{c}} {{\eta _B} = 1 - 0.064(B - 8)}\\ {{\eta _\alpha } = 1 + 0.26 \times \lg (\frac{{\hat \alpha }}{{0.68}})} \end{array}} \right.$ | (13) |
Based on Equation (13), the design chart of the coefficient(l)could be described in Figure 4.
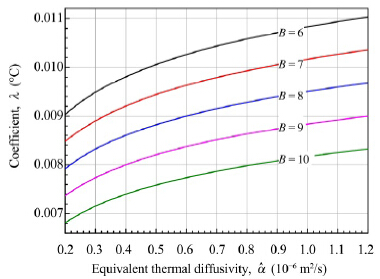 |
| Figure 4 Coefficient of temperature increment l |
Obviously, the factors affecting temperature increment include effective solar radiation, heat-transfer of air convection, pavement materials and pavement radiation. The equivalent thermal diffusivity($\hat \alpha $)reflects the impact of pavement materials and structure on temperature increment; and $\hat \alpha $ could be calculated by Equation (7) and referred in Table 1.
The heat-transfer coefficient(B)reflects the impact of heat-transfer of air convection on temperature increment. Based on the research of Yan(1984) and Mao et al.(2011), the value range of B is about 6 to 10 and the empirical formula of B could be expressed in the equation:
| $B = 5.5 + 1.6V$ | (14) |
in which V is wind-speed, m/s.
The effective solar radiation of one month(Qe)needs to consider the absorptivity of road surface, road trend and slope angle of road and could be expressed in the equation:
| ${Q_e} = Q \cdot \alpha \cdot \eta $ | (15) |
| Pavement materials | Asphalt concrete | Cement concrete | Ballastless roadbed |
| h | 0.9 | 0.5-0.7 | 0.9 |
The coefficient of slope angle(a)could be expressed in the equation(Wang, 2001):
| $\alpha = \left\{ {\begin{array}{*{20}{c}} {(ctg{\alpha _1} - ctg\beta \cdot \left| {\cos {\delta _1}} \right|)\sin {\alpha _1}\quad {\rm{shady}}}\\ {(ctg{\alpha _1} + ctg\beta \cdot \left| {\cos {\delta _1}} \right|)\sin {\alpha _1}\quad {\rm{sunny}}} \end{array}} \right.$ | (16) |
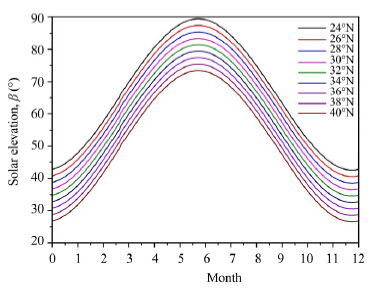 |
| Figure 5 Solar elevation(β) |
When the variety of solar radiation in each month is small, Q could be regarded as a constant; or Q could be described in the equation(Weng, 1986; Cha, 1996):
| $Q = {Q_0} + {Q_a} \cdot \sin ({\omega _a}t + {\varphi _2})$ | (17) |
in which Q0 is the average value of solar radiation of each month in a year; Qa is the amplitude of solar radiation of each month in oneyear; with the measured solar radiation in one month, Q0 and Qa could be obtained by fitting the least squares principle; wa is the angular frequency, equal to 2p/365d.
When there is a lack of the measured solar radiation, Q0 and Qa could be obtained by referring to He and Xie(2010); the solar radiation of one month could be designed with the equation:
| $Q = {Q_A} \cdot (0.213 + 0.569 \cdot S)$ | (18) |
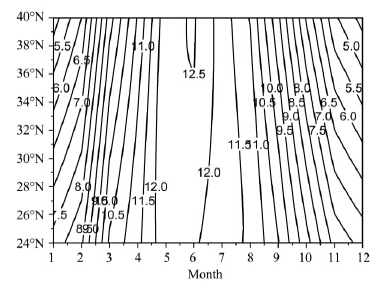 |
| Figure 6 Solarradiation(QA)of one month in Qinghai-Tibet Plateau(×100 MJ) |
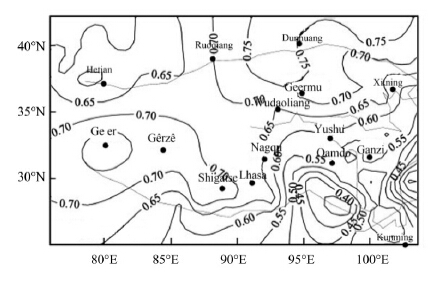 |
| Figure 7 Percentage of sunshine(S)in Qinghai-Tibet Plateau |
In a case of the Qinghai-Tibet Highway, subgrade width is 9 m and subgrade height is 2.5 m; the slope angle is p/4 and the geometry model of roadbed is presented in Figure 8. Soil thermodynamic parameters are presented in Table 3(Cao et al.,2014).
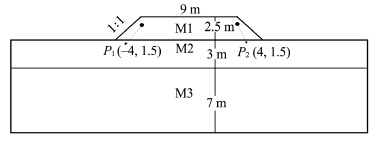 |
| Figure 8 Geometric model |
| Soil | r(kg/m3) | C(J/(kg×°C)) | k(W/(m×°C)) |
| M1 | 1, 870 | 1, 102 | 1.68 |
| M2 | 1, 708 | 1, 440 | 0.95 |
| M3 | 1, 050 | 2, 063 | 0.39 |
The boundary layer thicknesses are listed in Table 4 based on pavement structure and soil layers.
| Variable | Pavement | Roadbed slope | Natural ground |
| $\hat \alpha $(m2/s) | 6.2E−07 | 8.2E−07 | 3.9E−07 |
| $\delta _u $(m) | 0.39 | 0.45 | 0.31 |
In Beiluhe, Qinghai-Tibet Plateau, the latitude is 34.9°N and the longitude is 92.9°E, thus, solar radiation could be designed based on Figures 6 and 7. The absorptivity of pavement, subgrade slope and natural ground are 0.9, 0.7 and 0.6, respectively. The slope angle(a1)is 45°; the angle of the road trend(d1)is 70.9°; so the coefficient of slope angle(a)could be designed according to Equation (16). The latent heat(Qw)of vaporization should be deducted from the effective solar radiation. The design of temperature increment(Ti)is expressed in Table 5.
| Parameter | Time(Month) | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| QA(MJ) | 572 | 682 | 944 | 1, 091 | 1, 245 | 1, 248 | 1, 177 | 1, 121 | 963 | 772 | 600 | 529 | |
| Q(MJ) | 330 | 394 | 545 | 630 | 719 | 720 | 679 | 647 | 556 | 445 | 346 | 305 | |
| b | 33.6 | 41.3 | 52.3 | 64.1 | 73.4 | 78.3 | 77.0 | 70.1 | 59.7 | 48.1 | 37.9 | 32.2 | |
| a | Shady | 1.05 | 0.97 | 0.89 | 0.82 | 0.78 | 0.76 | 0.76 | 0.79 | 0.84 | 0.91 | 1.00 | 1.07 |
| Sunny | 0.36 | 0.44 | 0.53 | 0.60 | 0.64 | 0.66 | 0.65 | 0.62 | 0.57 | 0.50 | 0.41 | 0.34 | |
| Qw(MJ) | 4 | 4 | 6 | 10 | 30 | 60 | 76 | 64 | 37 | 10 | 3 | 3 | |
| Qe(MJ) | Pavement | 297 | 354 | 490 | 567 | 647 | 648 | 611 | 582 | 500 | 401 | 312 | 275 |
| Shady slope | 240 | 264 | 332 | 351 | 360 | 320 | 286 | 294 | 290 | 275 | 241 | 226 | |
| Sunny slope | 79 | 118 | 195 | 252 | 291 | 272 | 235 | 218 | 185 | 145 | 97 | 69 | |
| Ground | 194 | 232 | 321 | 368 | 401 | 372 | 332 | 324 | 296 | 257 | 205 | 180 | |
| Ti(°C) | Pavement | 3.15 | 3.76 | 5.20 | 6.01 | 6.86 | 6.88 | 6.49 | 6.18 | 5.31 | 4.25 | 3.31 | 2.92 |
| Shady slope | 2.62 | 2.89 | 3.63 | 3.84 | 3.94 | 3.50 | 3.12 | 3.22 | 3.18 | 3.01 | 2.63 | 2.48 | |
| Sunny slope | 0.87 | 1.30 | 2.14 | 2.76 | 3.18 | 2.97 | 2.57 | 2.39 | 2.03 | 1.59 | 1.06 | 0.76 | |
| Ground | 1.95 | 2.34 | 3.22 | 3.70 | 4.03 | 3.74 | 3.33 | 3.26 | 2.98 | 2.58 | 2.06 | 1.81 | |
| Ta(°C) | −11.81 | −10.60 | −6.73 | −1.25 | 4.38 | 8.65 | 10.41 | 9.20 | 5.33 | −0.15 | −5.78 | −10.05 | |
Based on Equation (1), the upper boundary condition could be described in Equation (19):
| $T(t) = {T_0} + A \cdot \sin (\frac{{2{\rm{\pi }}}}{{365}} \cdot t + {\varphi _0})$ | (19) |
For different position, the parameters could be selected in Table 6.
| Parameter | Pavement | Shady slope | Sunny slope | Ground |
| Ta(°C) | 4.33 | 2.47 | 1.27 | 2.22 |
| A | 12.90 | 11.46 | 12.04 | 11.89 |
| j0 | 1.43 | 1.41 | 1.42 | 1.42 |
| The bottom condition of temperature field is constant, −2 °C. | ||||
The measured value and simulated value of soil temperature at a depth of 0.6 m are listed in Figure 9; and at five years after the subgrade was built, the temperature fields of subgrade in January and July are shown in Figure 10.
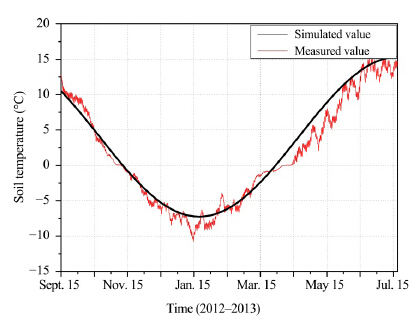 |
| Figure 9 Measured and simulated values of soil temperature at a depth of 0.6 m(in 2012-2013) |
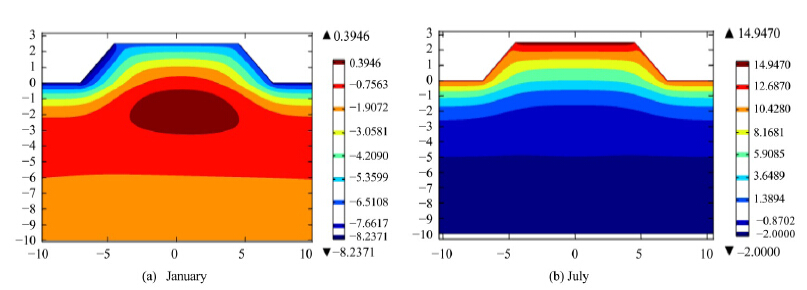 |
| Figure 10 Contour map of temperature field in subgrade(in the fifth year) |
As shown in Figure 10, in January, a warming area develops in the subgrade. Based on the comparison of Figure 9, simulated result of temperature field in the subgrade is accurate. According to Figures 8, 10 and 11, the asymmetry of temperature field is notevident and the difference value of temperature in points P1 and P2 is less than 2 °C. This is because the road trend is 70.9º. In fact, the temperatures in sunny and shady road slopes are related to the road trend. Varying the road trend and maintaining the other simulation settings in upper numerical test, the minimum temperatures of P1 and P2(occurring around January)are shown in Figure 11. In Figure 11, when the road trend is 0°, the temperature difference of P1 and P2 is the largest, about 5.1 °C.
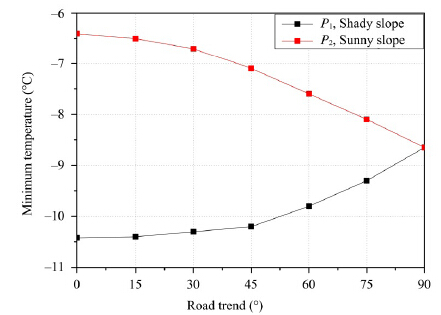 |
| Figure 11 Minimum temperatures of P1 and P2 in one year with diffident road trends |
Following the aforementioned procedure, the long term behavior of thermal conduction in any subgrade of highway or railway in permafrost region can be analyzed.
6 ConclusionsIn this paper, a method in the form of equations and design charts is proposed to determine the upper thermal boundary of subgrade where the daily fluctuation of temperature is negligible. The upper thermal boundary of subgrade is determined by two parameters, i.e., boundary layer thickness and the temperature increment. For typical designs of highway or railway, the boundary layer thicknesses are calculated and listed. Further, the empirical equation and design chart for determining the temperature increment are given in which the following factors are addressed, including solar radiation, equivalent thermal diffusivity and convective heat-transfer coefficient. Using these equations or design charts, the boundary layer thickness and temperature increment can be easily determined and used in the simulation of long-term temperature fields of subgrade.
An example is presented to demonstrate the selection process of the upper thermal boundary in detail and the results prove that the proposed method for determining the upper thermal boundary of subgrade is accurate and practical.
Acknowledgments: This research is supported by the National Natural Science Foundation of China(Nos. 51378057, 41371081, and 41171064) and the National Key Basic Research Program of China(973 Program, No. 2012CB026104).| Bai QB, LiX, Tian YH, 2015. Upper boundary conditions in the long-term thermal simulation of subgrade.Chinese Journal of Geotechnical Engineering (in press). |
| Cao YB, Sheng Y, Wu JC, et al., 2014. Influence of upper boundary conditions on simulated groundtemperature field in permafrost regions. Journal of Glaciology and Geocryology, 36(4): 802-809. |
| Cha LS, 1996.A study on spatial and temporal variation of solar radiation in China.ScientiaGeographicaSinica, 16(3): 223-237. |
| He QH, Xie Y, 2010.Research on the climatological calculation method of solar radiation in China. Journal of Natural Resources, 25(2): 308-319. |
| Lei XQ, 2011.Determination of specific heat capacity of material (Asphalt, Concrete) for plateau roadbed.Science and Technology, 3: 67-68. |
| Mao XS, Lu L, Hou ZJ,et al., 2011. Text and numerical simulation on subgrade temperature field of cement concrete pavement structure. Journal of Chang'an University(Natural Science Edition), 31(2): 1-5. |
| Qian BJ, Wu YW, Chang JF, et al., 1983.Heat Concise Manual. Beijing: ChinaHigher Education Press. |
| Wang LJ, 2005. The structure of pavement in west China.Master's Dissertation of Chang'an University,Xi'an, China. |
| Wang TX, 2001.Research on Calculation Principle and Critical Height of Subgrade in Permafrost Regions.Ph.D.Thesis ofChang'an University, Xi'an, China. |
| Weng DM, 1986. Climatical method for direct solar radiation calculation and its distribution over China.ActaEnergiaeSolaris Sinica, 7(2): 121-130. |
| Xu XZ, Wang JC, Zhang LX, 2001. Permafrost Physics. Beijing: Science Press. |
| Yan ZR, 1984. Analysis of the temperature field in layered pavement system.Journal of Tongji University, 3: 76-85. |
| Zhang HB, Zou L, Ji XP, 2011. Experimental study on the thermal conductivity of asphalt mixtures. Highway, 10:50-51. |
| Zhang XD, 2012. Railway Engineering. Beijing: China Railway Publishing House. |
| Zhu LN, 1988. Study of the adherent layer on different types of ground in permafrost regions on theQinghai-Xizang Plateau. Journal of Glaciology and Geocryology, 10(1): 8-14. |
 2015, 7
2015, 7


