Article Information
- SiWei He, ZhuoTong Nan, YuTing Hou. 2015.
- Accuracy evaluation of two precipitation datasets over upper reach of Heihe River Basin, northwestern China
- Sciences in Cold and Arid Regions, 7(2): 157-169
- http://dx.doi.org/10.3724/SP.J.1226.2015.00157
Article History
- Received: July 12, 2014
- Accepted: November 21, 2014
2. Civil and Architectural Engineering Department, University of Wyoming, Laramie, WY 82071, USA;
3. Shiyan Environmental Protection Monitoring Station, Shiyan, Hubei 442000, China
1 Introduction
Hehei River is the second largest inl and river of China, and plays an important role in sustaining the development of ecology, agriculture, industry, and animal husb and ry within the basin. A lot of research on economy(Zhou and Yang, 2006), ecology(Li et al.,2001; Ma and Frank, 2006; Feng et al.,2013; Wen et al.,2013), hydrology(Liu and Kotoda, 1998; Kang et al.,1999; Wang et al.,2009, 2013; Chen et al.,2013), and meteorology(Ma et al.,2010)have been performed in this basin. In order to further implement the hydrological and ecological research in the Heihe River Basin(HRB), a major research program was launched from the National Natural Science Foundation of China(NSFC), named Integrated Research of Ecological-Hydrological Processes in the Heihe River Watershed(Li et al.,2013). One important objective of this program is to study the water cycle and energy exchange in HRB with hydrological and l and surface models. The basic requirement of model application is accurate forcing data. As Cosgrove et al.(2003) pointed out, regardless of sophisticated description of l and processes in the model and accurate boundary and initial conditions provided, the model would not produce realistic simulation if the forcing data were not accurate.
The upper reach of HRB is the runoff yield area and is located in an alpine cold region. There are a limited number of hydrological and meteorological sites available for this area. Because of complex mountainous topography and high elevation, the meteorological forcing data, especially precipitation data, are insufficient to represent the entire area. The simple geo-statistical interpolation method generally adopted to extend site observations to areal coverage appeared poor in performance. Therefore, the main strategy in obtaining forcing data for the l and surface model(LSM)is to use reanalysis global datasets, such as the extensively used Global L and Data Assimilation System(GLDAS)forcing dataset, with proper downscaling methods to a desired resolution. The China Meteorological Forcing Dataset(hereafter ITP data)is an open dataset that covers the Chinese continent and was produced by merging a variety of data sources(Chen et al.,2010; He, 2010). This dataset currently covers the period of 1979-2010, with a spatial resolution of 0.1 degree and a temporal resolution of 3-hour. Chen et al.(2010) reported that over the Qinghai-Tibet Plateau, the simulation error of surface temperature could decrease by 2 K using ITP precipitation instead of GLDAS precipitation. GLDAS was developed by the National Aeronautics and Space Administration(NASA), coupling three alternative LSMs and merging ground and satellite observed data. GLDAS precipitation data got extensive worldwide uses(Gottschalck et al.,2005; Qian et al.,2006; Sheffield et al.,2006; Syed et al.,2008). However, for the arid basin such as HRB, the applicability of ITP and GLDAS precipitation data remains unclear. As precipitation is the main source of water in arid areas, accurate precipitation plays the most important role in a good simulation(Beven, 2001). A comprehensive evaluation of ITP and GLDAS precipitation is necessary before using them in models.
As-Syakur et al.(2011) compared TRMM multisatellite precipitation analysis(TMPA)products with daily and monthly gauge data over Bali and concluded that the data from TMPA were potentially usable to replace rain gauge data, especially for monthly data. In their study, the linear correlation coefficient, mean bias, root mean square error, and mean absolute error were used as evaluation metrics. Gourley et al.(2011) evaluated rainfall data that were estimated from NEXRAD, operational rain gauges, TRMM TMPA, and ERSIANN-CCS via a calibrated hydrologic model. In the study of Nan et al.(2010), six years of hourly and daily precipitation time series data from NEXRAD and NLDAS were investigated on their spatial similarities over a sub-region of the Ohio River Basin. In that study, three spatial metrics were used: Cohens Kappa coefficient, Forecast Quality Index(FQI), and displacement-based Forecast Quality Measure(FQM)respectively. Hou et al.(2013) compared the precipitation data calculated from WRF(Weather Research and Forecasting model)with GLDAS over the upper reach of the Heihe River Basin and confirmed that both datasets were able to capture precipitation spatial distribution. That study discovered that WRF produced annual precipitation were much closer to observations than GLDAS while producing higher correlation of GLDAS than that of WRF.
However, in terms of well serving hydrological and l and surface modeling, all these evaluation methods are not comprehensive. In order to fully evaluate precipitation data for hydrological and l and surface modeling purposes, the following aspects should be followed:(1)Evaluating data at varying time scales, as LSMs usually run at different time scales such as hourly, 3-hour, and daily;(2)In addition to magnitude, precipitation occurrence frequency and temporal distribution also need to be considered, as these aspects will impact heat and water fluxes; and (3)considering spatial distribution of precipitation that would have significant effects on internal hydrologic circulation.
In this paper, ITP and GLDAS precipitation data in the period of 2004-2009 were evaluated over the upper reach of Heihe River Basin, which is a typical cold mountainous area in an arid watershed. During the process, a comprehensive approach was proposed to take into account multiple scales, trend, magnitude, annual allocation, precipitation event matching, and spatial distribution. Meanwhile, the wavelet analysis was introduced to reveal the deviations of precipitation at varying frequency domains.
2 Study area and data 2.1 Study areaThe study area covers the upper reach area of Heihe River Basin(HRB)in northwestern China(Figure 1). The Heihe River is the second largest inl and river of China and flows through Qinghai, Gansu, and Inner Mongolia provinces. The basin is a typical arid watershed bounded between longitudes 98.56°E-101.16°E and latitudes 37.63°N-39.15°N. The HRB upper reach area, which is the runoff yield area of the entire watershed, covers an area of 10, 009 km2. There are two tributaries in the upper reach. The east tributary covers an area of 2, 452 km2 and is observed at the Qilian site(Figure 1), and the west tributary covers an area of 4, 589 km2 and is observed at the Zhamashike site(Figure 1). These two tributaries join at Huangzangsi and then discharge to the middle reach through the Yingluoxia site(Figure 1).
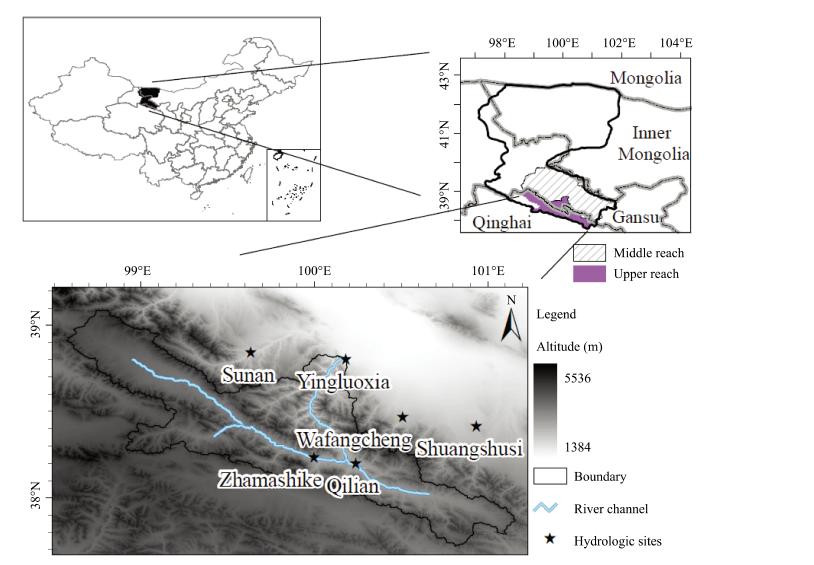
|
| Figure 1 Distribution of gauged hydrologic sites in and near the study area |
The ITP dataset st and s for the China Meteorological Forcing Dataset was produced by merging a variety of data sources, including observation records from China Meteorological Administration(CMA)stations, TRMM satellite precipitation analysis data(3B42), GLDAS precipitation data, GEWEX-SRB download shortwave radiation, and Princeton forcing data(Chen et al.,2010; He, 2010). Its spatial resolution is 0.1 degree and temporal resolution is 3-hour. The items included in this dataset are temperature, pressure, specific humidity, wind speed, downward shortwave and longwave radiation, and precipitation. This dataset currently covers the period of 1979-2010, and can be obtained from the Cold and Arid Regions Sciences Data Center at Lanzhou(http://westdc.westgis.ac.cn).
2.3 GLDAS datasetThe GLDAS-NOAH precipitation data, which are the result of merging Global Data Assimilation System(GDAS)data with NOAAs Climate Prediction Center Merged Analysis of Precipitation(CMAP)data, were used for this research. The GLDAS precipitation dataset was downloaded from ftp://hydro1.sci.gsfc.nasa.gov/data/s4pa/GLDAS_V1/. Its spatial resolution is 0.25 degree and temporal resolution is 3-hour. The precipitation amount was calculated by adding rainfall and snowfall rates. This precipitation data covers the period of 2004-2009(Hou, 2013).
Wang et al.(2011) drew a conclusion that GLDAS is of high quality for daily and monthly precipitation in the upper Second Songhua River Basin(USSP). However, according to the study of Yang et al.(2009), GLDAS precipitation data underestimated both precipitation occurrence and accumulated amount in M and al Govi of Mongolia. These studies show that the accuracy of GLDAS precipitation data may vary with region and an evaluation is necessary prior to use.
2.4 Observation dataThere are three hydrologic sites, Yingluoxia(YLX), Qilian(QL) and Zhamashike(ZM), within the upper reach of HRB and three other hydrologic sites, Sunan(SN), Wafangcheng(WFC) and Shuangshusi(SSS)nearby(Figure 1). The observed precipitation data in these sites were chosen as referenced values. The available record period of these sites were from 1990 to 2009.
2.5 Data pre-processingThe terrain in the study area is relatively complex, so the spatial resolution is set to 5 km to account for this heterogeneity. In this study, ITP and GLDAS precipitation data were identically downscaled into 5 km with the MicroMet model(Liston and Elder, 2006). The time period for evaluation is set to 2004 to 2009.
3 MethologyThe evaluation metrics in this paper can be classified into two categories. The first category is based on statistical indicators, while the second one is based on wavelet transform. Compared with previous studies on precipitation data accuracy evaluation, the proposed method in this study features four remarkable highlights.
1)Including frequently-used metrics in evaluating precipitation data accuracy, such as correlation coefficient, Nash-Sutcliffe efficiency coefficient(NSE), annual total precipitation and precipitation days, as well as considering precipitation variations at different time scales.
2)Adopting three weather forecasting indicators, namely, probability of detection(POD), false alarm ratio(FAR), and critical success index(CSI), which treat precipitation as a binary event.
3)Introducing wavelet transform to discompose precipitation time series and evaluating precipitation characteristics at different frequency domains.
4)Evaluating both magnitude and pattern of spatial distribution of precipitation.
3.1 Statistical metricsThe statistical metrics adopted are presented in Table 1. At the daily scale, ITP and GLDAS precipitation data were evaluated in terms of correlation with observation, predictive abilities, occurrence frequency, and temporal distribution features. In this process, the metrics were calculated for each year using daily comparisons of observations vs. GLDAS and ITP. At the same time, the average metrics of the six years were calculated. At the monthly scale, they were evaluated as per correlation with observation and magnitude. In this process, the metrics were not calculated for each year, but only the six years length using monthly comparisons of observations vs. GLDAS and ITP. At the yearly scale, annual precipitation error was used as the indicator. Apart from those, the spatial distribution on the upper reach of HRB was also investigated.
| Distribution | Period | Metrics |
| Temporal distribution | Yearly | Precipitation error |
| Monthly | Pearson correlation coefficient Nash-Sutcliffe efficiency coefficient | |
| Daily | Pearson correlation coefficient Nash-Sutcliffe efficiency coefficient Precipitation days Total precipitation between May and September Probability of detection(POD)False alarm ratio(FAR)Critical success index(CSI) | |
| Spatial distribution | Yearly | Spatial distribution of annual precipitation |
Owing to the ability of providing localized characteristics of non-stationary time series both in temporal and frequency domain, wavelet transform was widely used in hydrology and earth sciences(Daubechies, 1990; Foufoula-Georgiou and Kumar, 1994; Kumar and Foufoula-Georgiou, 1997; Sang, 2011). Sang et al.(2011) studied the factors influencing complexity of hydrologic series based on wavelet transform. Taking the El Nino-Southern Oscillation(ENSO)time series for example, a practical step-by-step guide of wavelet analysis to geoscience long-term data was given in the study authored by Torrence and Compo(1998). Through the wavelet transform, the precipitation data series can be decomposed by frequency, so that information at different frequency domains can be detected. This method can complement traditional statistical metrics(de Trad et al.,2002).
The following procedure is proposed. First, discrete wavelet transform was implemented on all three data series, namely, observed precipitation records, ITP precipitation, and GLDAS precipitation. Then, traditional metrics(Pearson correlation and NSE)were applied to decomposed series so as to discover data characteristics at various frequency domains.
4 Results 4.1 Statistical metrics 4.1.1 Daily scaleThe Pearson correlation coefficients(PCCs)are presented in Figure 2, where horizontal axes represent the study years from 2004 through 2009, and 6-year annual average of correlations, while vertical axes represent PCC. The dashed line indicates GLDAS data and solid line ITP data, respectively. Overall, all PCCs of GLDAS and ITP precipitation data against observations have no significant difference. However, the PCCs of ITP are slightly larger than those of GLDAS in the QL and ZM sites. Conversely, PCCs of GLDAS are slightly larger than those of ITP in the SSS site.
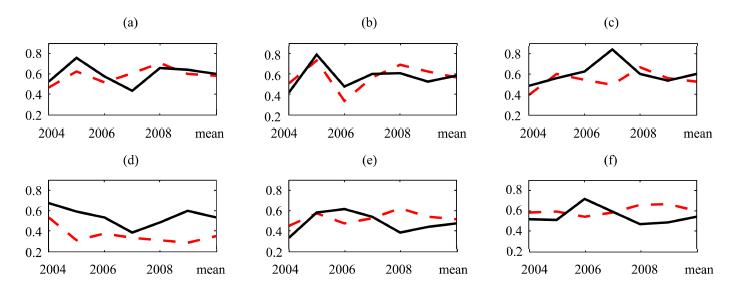
|
| Figure 2 Pearson correlation coefficients at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f); Dashed line indicates GLDAS and solid line indicates ITP |
The Nash-Sutcliffe efficiency coefficients(NSEs)are presented in Figure 3 where the horizontal axes are equivalent to those of Figure 2 and the vertical axes represent NSE. Figure 3 shows that NSEs present the same trends as PCCs at all six sites. However, since NSE takes into account not only change trend but also magnitude, NSEs hold relatively lower values. At the QL and ZM sites, NSEs of ITP are higher than those of GLDAS.
|
| Figure 3 Nash-Sutcliffe coefficients at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f); Dashed line indicates GLDAS and solid line indicates ITP |
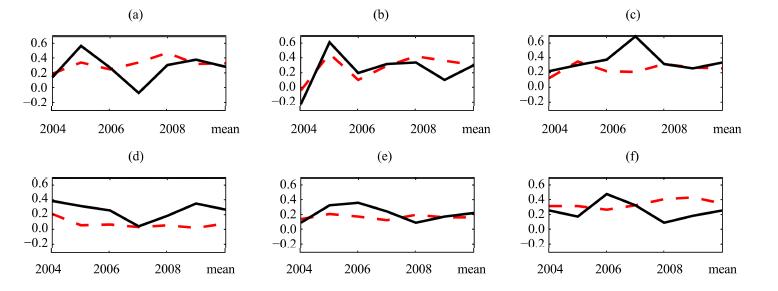
Precipitation days are the number of days that daily precipitation is greater than 0.1 mm. This metric reflects the agreement of precipitation temporal distribution. Figure 4 shows the relative errors of precipitation days of ITP and GLDAS against the observations. The horizontal axes are equivalent to those of Figure 2 while the vertical axes represent relative errors of precipitation days(%). In the calculating procedure, both positive and negative biases were taken into account. It can be seen that in all years, these two precipitation data have more precipitation days than observations, in particular the ITP data.
|
| Figure 4 Relative errors of precipitation days at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f). Dashed line indicates GLDAS and solid line indicates ITP |
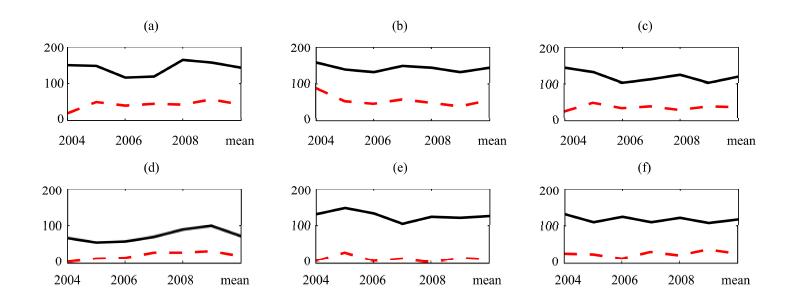
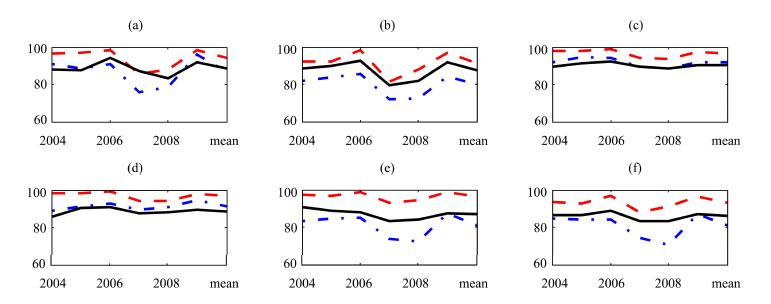
The temporal distribution of precipitation is non-uniform in the upper reach of HRB and precipitation is mainly concentrated in the months of May through September(Li et al.,2006). The proportion of precipitation amount in May through September in a whole year can also reflect the temporal feature of a dataset. Figure 5 presents the proportions of precipitation amount during May through September to annual precipitation, for ITP, GLDAS, and observations. In Figure 5, solid lines represent ITP, dashed lines represent GLDAS, and dash-dot lines represent observations. The horizontal axes are equivalent to those of Figure 2 and the vertical axes are the proportions(%). This reveals that ITP data are much closer to observation in terms of precipitation ratio during May through September, than GLDAS to observation, especially in the QL and ZM sites. The proportions with GLDAS are significantly larger and even up to 100% larger in some years.
|
| Figure 5 Proportions of precipitation amount during May through September in a whole year at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f); Solid line indicates ITP, dashed line for GLDAS and dashed-dot line for observation |
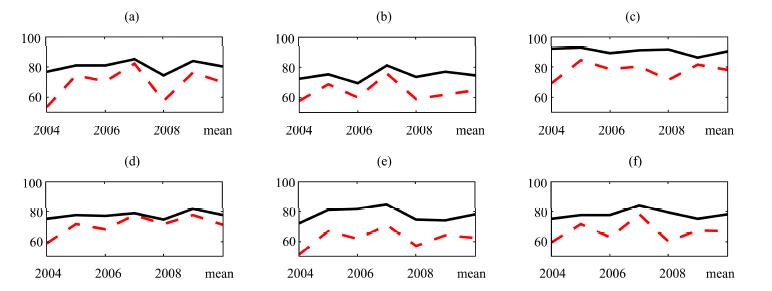
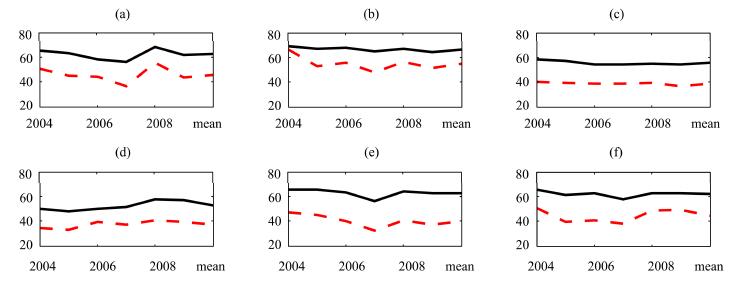
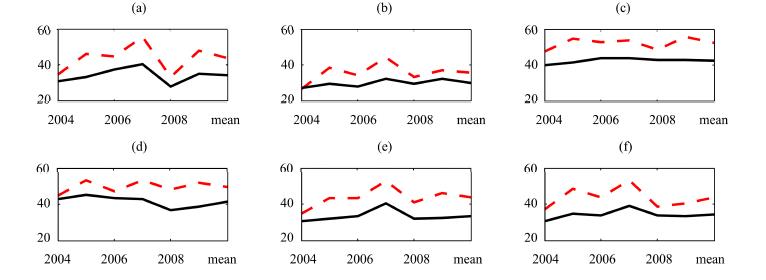
Probability of detection(POD), false alarm ratio(FAR), and critical success index(CSI)are three basic evaluation metrics that are often used in weather forecasting services. These metrics treat precipitation event as a binary event, that is, only two types, occurrence or nonoccurrence. POD is the percentage of all precipitation events which were warned for with a perfect score of 100%. FAR measures how often we issue false alarms and ideally we want this number to be 0.0%. It is obvious that over-prediction might achieve a high POD, but at the expense of a high FAR. Overall success can be expressed by CSI, which is a function of both POD and FAR. These three metrics were adopted in our method and the results are provided in Figures 6-8, respectively. The horizontal axes are equivalent to those of Figure 2 and the vertical axes represent POD(%), FAR(%), and CSI(%), respectively.
Based on Figures 6 and 7, it was found that both ITP and GLDAS showed over-prediction; moreover, compared with GLDAS, ITP has larger FAR, indicating ITP has serious over-prediction precipitation events. This finding is consistent with Figure 4, in which relative errors of precipitation days are positive and ITP has large relative errors than GLDAS. Figure 8 shows that GLDAS is much closer to observations than ITP is, if we ignore precipitation magnitude and treat precipitation as a binary event.
|
| Figure 6 Probabilities of detection at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f). Dashed line indicates GLDAS and solid line indicates ITP |
|
| Figure 7 False alarm ratios at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f). Dashed line indicates GLDAS and solid line indicates ITP |
|
| Figure 8 Critical success indices at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f). Dashed line indicates GLDAS and solid line indicates ITP |
In order to evaluate the accuracy of precipitation intensities at different levels, the data were divided into three categories, namely light(0.1-10 mm/day), moderate(10-25 mm/day), and heavy(>25 mm/day). According to the daily precipitation data from year 2004 to 2009, the annual average rain day of each level can be obtained(Table 2).
| Hydrologic site | Heavy(days) | Moderate(days) | Light(days) | ||||||||
| GLDAS | ITP | OBS | GLDAS | ITP | OBS | GLDAS | ITP | OBS | |||
| SN | 0.00 | 0.00 | 0.33 | 1.00 | 4.33 | 6.50 | 115.83 | 192.33 | 74.67 | ||
| YLX | 0.00 | 0.00 | 0.67 | 0.67 | 2.00 | 2.50 | 91.33 | 141.83 | 56.50 | ||
| QL | 0.00 | 0.00 | 1.00 | 2.67 | 5.00 | 10.00 | 128.50 | 205.00 | 85.33 | ||
| ZM | 0.00 | 0.00 | 1.17 | 2.00 | 4.50 | 11.17 | 126.83 | 181.17 | 94.50 | ||
| WFC | 0.00 | 0.00 | 1.50 | 1.33 | 2.83 | 13.33 | 107.17 | 217.00 | 82.33 | ||
| SSS | 0.33 | 0.33 | 2.00 | 3.17 | 6.17 | 8.83 | 121.67 | 208.00 | 88.00 | ||
From Table 2, it can be seen that both ITP and GLDAS underestimate rain days for heavy and moderate precipitation. However, the days of light precipitation are overestimated by both ITP and GLDAS. The difference in the moderate level is larger for GLDAS than ITP while the difference in the light level is smaller for GLDAS than ITP.
4.1.2 Monthly scaleNSE and PCC were selected as metrics at the monthly scale. In Figure 9, the horizontal axes indicate selected sites. Differing from what we did in the analysis of the daily scale, we calculated the metrics for the whole six years at the monthly scale instead of for each year. It can be seen from Figure 9a that at all sites, the PCCs of ITP against observations are larger than those of GLDAS except at the SSS site, where the two PCCs are almost identical. However, NSEs of ITP are larger than GLDAS without exception. It is also obvious that NSEs of ITP at the QL and ZM sites are larger than other sites.
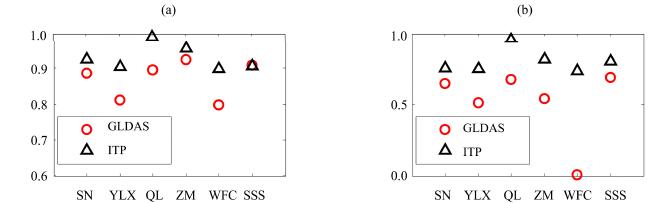
|
| Figure 9 Correlation coefficients at a monthly scale.(a)PCC and (b)NSE |
The yearly precipitation amount is an important indicator. In our method, it was evaluated via relative error of annual precipitation against observed. For each site, relative errors of annual precipitation are presented in Figure 10 where the horizontal axes are equivalent to those of Figure 2 and vertical axes represent relative errors(%). There is a distinct smaller relative error of annual precipitation of ITP than those of GLDAS. For all sites, GLDAS appeared significantly smaller than observations. ITP was much closer to the observed records at the QL site.
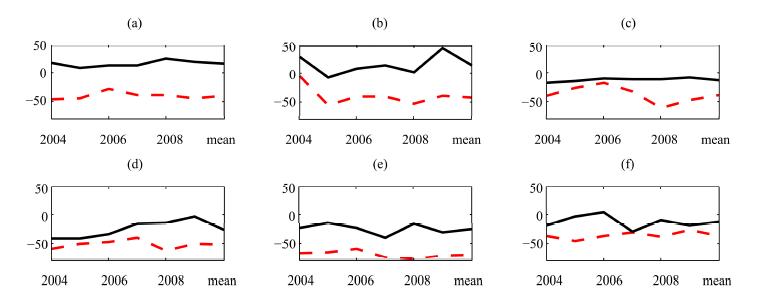
|
| Figure 10 Relative error of annual precipitation at observation sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f); Dashed line indicates GLDAS and solid line indicates ITP |
The wavelet transform with db4 wavelet function and four levels was implemented on observations, ITP, and GLDAS precipitation data, respectively. After the transform, a low-frequency and four high-frequency time series can be obtained. We compared ITP and GLDAS low-frequency series with observation low-frequency series and also for the four high-frequency series. Conventional statistical metrics such as NSE and PCC are used to those decomposed time series at various frequency levels. The results are displayed in Figure 11, where the horizontal axes represent frequencies while the vertical axes represent PCCs or NSEs as annotated. The a4 denotes the low-frequency part, d1-d4 denote the four high-frequency parts. As shown in the low-frequency part, the PCCs of ITP against observations and those of GLDAS are almost identical at all sites, while, the NSEs of ITP are slightly larger than those of GLDAS. In the high-frequency parts, the relationship is complex.
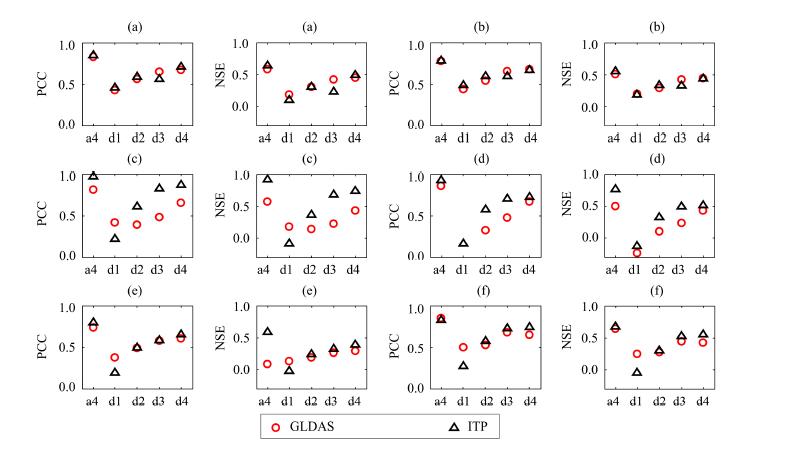
|
| Figure 11 Relationship of correlation coefficients versus observations at different sites. SN(a), YLX(b), QL(c), ZM(d), WFC(e), and SSS(f) |
Figure 12 presents the spatial distribution of annual precipitation from 2004 to 2009 as well as annual average. In order to show the relationship between spatial distribution and topography, the valley lines are also displayed. The following information can be concluded.
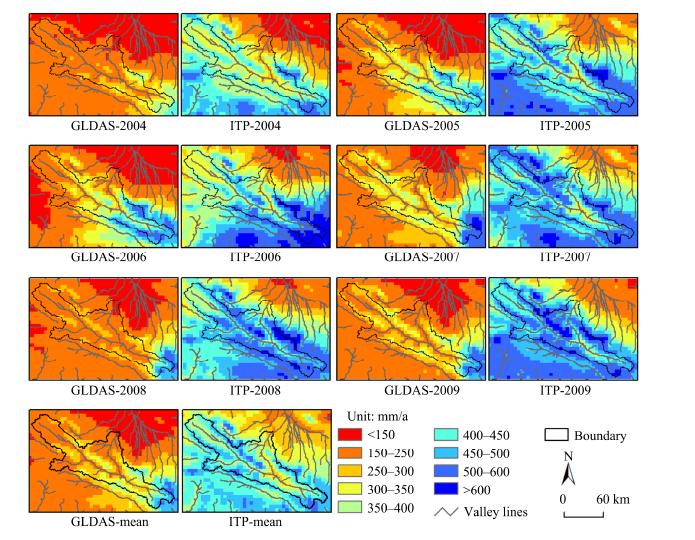
|
| Figure 12 Spatial distributions of annual and annual average precipitation |
1)The spatial distribution of precipitation in this region is uneven and varies remarkably. Both ITP and GLDAS precipitation data show that the source area of the Heihe River east tributary has abundant precipitation and precipitation declines from east to west. This is coincident with previous studies(Tang, 1985; Zhu and Wang, 1996; Ding et al.,1999; Zhang and Li, 2004; Li, 2008; Li et al.,2009).
2)It also depicted that terrain controlled precipitation distribution over the study area with both ITP and GLDAS. Low altitudes and river valley regions have less precipitation than high altitudes. This indicates that in the mountainous area, total precipitation amount increases along with altitude. A similar law was also discovered in previous studies(Tang, 1985; Zhu and Wang, 1996; Ding et al.,1999; Zhang and Li, 2004; Li, 2008; Li et al.,2009).However, the lapse rate of GLDAS is smaller than that of ITP.
3)In most regions, GLDAS has smaller annual precipitation than ITP. This phenomenon is also detected in Figure 10 which shows the relative errors of annual precipitation at individual sites.
5 DiscussionBased on a set of evaluation metrics, the characteristics of ITP and GLDAS precipitation data are presented in a more comprehensive and systematic way.
According to the comparison results of PCC and NSE(Figures 2 and 3), precipitation data of ITP and GLDAS have similar accuracy. However, in the QL and ZM sites, ITP has better quality than GLDAS because the QL site is a national weather site and the observations of QL was assimilated into the ITP data. The ZM site is near QL and its accuracy was also improved due to the interpolation process. This neighborhood effect is also reflected in both Figures 3 and 5. Compared with observations, the relative errors of precipitation days of ITP data are much larger than those of GLDAS(Figure 4). The occurrence of a precipitation event in ITP was determined by TRMM 3B42. Wu et al.(2013) evaluated coarse-resolution TRMM 3B42 in the HRB to some degree. In their study, only annual precipitation and correlation coefficient at the monthly scale were presented, however, precipitation days and the correlation coefficient at the daily scale were ignored. Therefore, their study cannot confirm the temporal distribution of TRMM 3B42 precipitation although its annual amount might be acceptable. Based on the findings from the ITP data, it implied that large deviations existed for TRMM 3B42 and observations in terms of temporal distribution. This study also confirms that precipitation in the Qilian mountainious region is mainly concentrated in the months of May through September as shown in Figure 5. Also, Figure 5 shows errors of both ITP and GLDAS in terms of temporal distribution compared with site observations; the errors are especially large with GLDAS. However, it should be noted that large errors in Figure 5 do not mean large biases of precipitation amounts because they are proportional which are not dependent on the actual amount of the annual total. POD(Figure 6), FAR(Figure 7), and CSI(Figure 8)show that the ITP precipitation is seriously over-predicted, and again verified that TRMM 3B42 has a large bias in representing the temporal distribution of precipitation over the upper reach of HRB.
The wavelet transform demonstrates that ITP and GLDAS are nearly identical in the low-frequency domain and the main differences occur in the high-frequency domains. This is because the precipitation series is with strong noises. The low-frequency domain represents the periodical changes, relatively steady and easy to predict. The high-frequency domains represent the details and have a great influence on the precipitation accuracy. Our experiment confirmed that both datasets had no problem in representing long term precipitation periodical changes.
Compared with the daily scale, the correlation coefficients of either ITP or GLDAS against observation were significantly improved(Figure 9)at a monthly scale. However, NSE of GLDAS at the WFC site is very small but its correlation is relatively good. This implies a well matched trend but the magnitude differed. Actually, the spatial pattern analysis confirmed that GLDAS precipitation is much smaller than observation in terms of amount. But because ITP assimilated site observations, it had a very good performance in the QL and ZM sites which are inside the upper reach.
The relative error of annual precipitation(Figure 10)discovered that GLDAS underestimated precipitation with large deviations. Meanwhile, ITP had relatively small biases with some positive and some negative. The ITP data had best accuracy in the QL site than other sites. This may attribute to the mergence of China Meteorological Administration site observations into the dataset.
In the upper reach of HRB, precipitation sites are very limited and hard to capture large spatial heterogeneity. As we know, topography and climate factors have effects on the spatial distribution of precipitation. Previous studies(Ding et al.,1999; Li et al.,2006)have pointed out that since the orographic uplift in the middle Qilian Mountains, this region received increased precipitation and formed a wet isl and in the arid area. By considering large-scale geographic factors, altitude, and local topographic factors, Tang(1985) depicted a contour map of annual precipitation distribution and concluded the characteristics of spatial distribution in this region on basis of precipitation records of many years. Li(2008) divided the Qilian Mountains into four zones based on precipitation, topography, and other weather conditions and summarized precipitation characteristics of each zone as per the theory of climatic regionalization. All these existing studies are from the perspective of meteorology and on the basis of observation records, taking many factors into consideration, and can be treated as credible evidence regarding the precipitation spatial distribution over the upper reach of HRB.
Our study shows that both ITP and GLDAS precipitation have some similar spatial distribution patterns. The abundant precipitation zone in the east tributary is near the Lenglong range, which is the area with most precipitation in the Qilian Mountains according to the climatological records. This area is not only of high altitude but also in the windward side of the plateau summer monsoon(Tang, 1985). The southwest and southeast monsoons impact precipitation not only in the Qilian Mountains but also as far as the upper reach of HRB. These monsoons produce abundant rainfall, but decrease from west to east. From the view of mountain precipitation formation, as the condensation level of convective precipitation is very high, most precipitation occurred at high altitudes(Tang, 1985). These main characteristics over the Qilian Mountains were captured by both ITP and GLDAS precipitation data.
In order to further quantitatively evaluate the spatial distribution of ITP and GLDAS precipitation in the study area, two previous studies were referenced. First, the spatial distributions of ITP and GLDAS were compared with the contour map of annual precipitation(Tang, 1985). This comparison shows that ITP was relatively reasonable while GLDAS underestimated annual precipitation in most regions. According to the study of Li(2008), the study area which is located in the east middle zone of the Qilian Mountains, is a semi-humid type with an annual precipitation around 377.6 mm. This is roughly matched by ITP while GLDAS is obviously smaller than the number in most parts of the study area except for the east tributary source area.
6 ConclusionsIn this paper, a comprehensive approach including multiple statistical metrics, multiple time scales, and wavelet transform was proposed and applied to assess the accuracy of ITP and GLDAS precipitation data(2004-2009)over the upper reach of Heihe River Basin(HRB). In addition, the spatial distribution of ITP and GLDAS precipitation was evaluated. Some conclusions can be drawn from this paper.
1)Both ITP and GLDAS precipitation data well represent the trend of precipitation over the upper reach of HRB. However, GLDAS underestimated precipitation in most regions of the study area except for the east tributary source area. In addition, the temporal distribution of ITP and GLDAS annual precipitation did not match the observations well; the proportions of total precipitation in May through September in a year were higher than observations. GLDAS represented the temporal distribution even worse.
2)The accuracy of ITP was improved for assimilating China Meteorological Administration(CMA)sites data. This was especially obvious in or near the grids where CMA sites are located. However, ITP precipitation data overestimated the precipitation days. The same phenomenon was also revealed by the weather forecast metrics. Considering the inheritance of ITP and TRMM 3B42, it implied that the TRMM 3B42 precipitation data cannot capture the actual precipitation events precisely.
3)Through wavelet transform, it is shown that both ITP and GLDAS can well match the observation at low frequency domain. At the high frequency domains, these two precipitation data varied with sites except for the same change trend.
4)Both ITP and GLDAS precipitation data reflected the basic characteristics of precipitation spatial distribution in the study area. This was verified with previous studies which were from the perspective of meteorology. Compared with previous studies, our study revealed that ITP precipitation data were more reasonable than GLDAS in terms of spatial pattern. Also, the original spatial resolution of ITP(0.1 degree)is much finer than that of GLDAS(0.25 degree).
The approach proposed in this paper can comprehensively characterize every important aspect of precipitation data such as trend, magnitude, annual allocation, event matching, frequency, and spatial distribution as well as assess from various scales such as daily, monthly, and yearly. The proposed approach can also be applied to evaluate the accuracy of precipitation over other regions. Although this study recommended the use of ITP precipitation in the upper reach of HRB, it is still necessary to develop more accurate precipitation data with new techniques to meet the requirement of high resolution l and surface modeling. For example, Pan et al.(2012) proposed a precipitation data assimilation method that merged Doppler radar data. Hopefully, these new methods may lead to new and better precipitation data for complex terrain areas.
Acknowledgments: This study was supported by NSFC(91125006) and partially by state key laboratory grant(SKLFSE201009). The China Meteorological Forcing Dataset used in this study was developed by Data Assimilation and Modeling Center for Tibetan Multi-spheres, Institute of Tibetan Plateau Research, Chinese Academy of Sciences. The author appreciates the efforts involved in the development of the dataset. We also thank the anonymous reviewers and editors of this journal for their constructive comments.| As-Syakur A, Tanaka T, Prasetia R, et al., 2011. Comparison of TRMM multisatellite precipitation analysis (TMPA) products and daily-monthly gauge data over Bali. International Journal of Remote Sensing, 32(24): 8969-8982. DOI: 10.1080/01431161.2010.531784. |
| Beven K, 2001. How far can we go in distributed hydrological modelling? Hydrology and Earth System Sciences, 5(1): 1-12. DOI: 10.5194/hess-5-1-2001. |
| Chen H, Nan Z, Wang S, et al., 2013. Simulating the water-heat processes on typical sites in the mountainous areas of the upper reaches of the Heihe River. Journal of Glaciology and Geocryology, 35(1): 126-137. |
| Chen Y, Yang K, Zhou D, et al., 2010. Improving the Noah land surface model in arid regions with an appropriate parameterization of the thermal roughness length. Journal of Hydrometeorology, 11(4): 995-1006. DOI: 10.1029/2011jd015921. |
| Cosgrove BA, Lohmann D, Mitchell K, et al., 2003. Real-time and retrospective forcing in the North American land data assimilation system (NLDAS) project. Journal of Geophysical Research-Atmospheres, 108(D22): 8842. DOI: 10.1029/2002jd003118. |
| Daubechies I, 1990. The wavelet transform time-frequency localization and signal analysis. IEEE Transactions on Information Theory, 36(5): 961-1005. DOI: 10.1109/18.57199. |
| de Trad C, Fang Q, Cosic I, 2002. Protein sequence comparison based on the wavelet transform approach. Protein Engineering, 15(3): 193-203. DOI: 10.1093/protein/15.3.193. |
| Ding Y, Ye B, Zhou W, 1999. Temporal and spatial precipitation distribution in the Heihe catchment, northwest China, during the past 40 a. Journal of Glaciology and Geocryology, 21(1): 42-48. |
| Feng Q, Liu W, Xi H, 2013. Comprehensive evaluation and indicator system of land desertification in the Heihe River Basin. Natural Hazards, 65(3): 1573-1588. DOI: 10.1007/s11069-012-0429-5. |
| Foufoula-Georgiou E, Kumar P, 1994. Wavelets in Geophysics (Vol. 4). Academic Press, pp. 373. |
| Gottschalck J, Meng J, Rodell M, et al., 2005. Analysis of multiple precipitation products and preliminary assessment of their impact on global land data assimilation system land surface states. Journal of Hydrometeorology, 6(5): 573-598. DOI: 10.1175/JHM437.1. |
| Gourley JJ, Hong Y, Flamig ZL, et al., 2011. Hydrologic evaluation of rainfall estimates from radar, satellite, gauge, and combinations on Ft. Cobb Basin, Oklahoma. Journal of Hydrometeorology, 12(5): 973-988. DOI: 10.1175/2011jhm1287.1. |
| He J, 2010. Development of a surface meteorological dataset of China with high temporal and spatial resolution. Thesis of Chinese Academy of Sciences. |
| Hou Y, 2013. Comparative evaluation of precipitation forcing data over the upper Heihe river basin and runoff responses using Noah LSM. Thesis of Lanzhou University, China. |
| Hou Y, Nan Z, Pan X, 2013. Comparative evaluation of wrf and gldas precipitation data over the upper Heihe River Basin. Journal of Lanzhou University (Natural Sciences), 49(4): 437-447. |
| Kang ES, Cheng GD, Lan YC, et al., 1999. A model for simulating the response of runoff from the mountainous watersheds of inland river basins in the arid area of northwest China to climatic changes. Science in China (Series D: Earth Sciences), 42: 52-63. DOI: 10.1007/bf02878853. |
| Kumar P, Foufoula-Georgiou E, 1997. Wavelet analysis for geophysical applications. Reviews of Geophysics, 35(4): 385-412. DOI: 10.1029/97rg00427. |
| Li H, Wang K, Jiang H, et al., 2009. Study of the precipitation in the Heihe River Basin: Progress and prospect. Journal of Glaciology and Geocryology, 31(2): 334-341. |
| Li X, Cheng GD, Liu SM, et al., 2013. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bulletin of the American Meteorological Society, 94(8): 1145-1160. DOI: 10.1175/BAMS-D-12-00154.1. |
| Li X, Lu L, Cheng GD, et al., 2001. Quantifying landscape structure of the Heihe River Basin, north-west China using FRAGSTATS. Journal of Arid Environments, 48(4): 521-535. DOI: 10.1006/jare.2000.0715. |
| Li Y, 2008. Study and analysis on climatic characteristics of precipitation and it causes over Qilian Mountains. Thesis of Lanzhou University, China. |
| Li Z, Yang J, Li R, et al., 2006. The climatic analysis on weather modification in mid-section of Qilian Mountain and available weather patterns. Arid Meteorology, 24(1): 23-27. |
| Liston GE, Elder K, 2006. A meteorological distribution system for high-resolution terrestrial modeling (MicroMet). Journal of Hydrometeorology, 7(2): 217-234. DOI: 10.1175/jhm486.1. |
| Liu J, Kotoda K, 1998. Estimation of regional evapotranspiration from arid and semi-arid surfaces. Journal of the American Water Resources Association, 34(1): 27-41. DOI: 10.1111/j.1752-1688.1998.tb05958.x. |
| Ma M, Frank V, 2006. Interannual variability of vegetation cover in the Chinese Heihe River Basin and its relation to meteorological parameters. International Journal of Remote Sensing, 27(16): 3473-3486. DOI: 10.1080/01431160600593031. |
| Ma Y, Menenti M, Feddes R, 2010. Parameterization of heat fluxes at heterogeneous surfaces by integrating satellite measurements with surface layer and atmospheric boundary layer observations. Advances in Atmospheric Sciences, 27(2): 328-336. DOI: 10.1007/s00376-009-9024-4. |
| Nan Z, Wang S, Liang X, et al., 2010. Analysis of spatial similarities between NEXRAD and NLDAS precipitation data products. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 3(3): 371-385. DOI: 10.1109/jstars.2010.2048418. |
| Pan XD, Tian XJ, Li X, et al., 2012. Assimilating Doppler radar radial velocity and reflectivity observations in the weather research and forecasting model by a proper orthogonal-decomposition- based ensemble, three-dimensional various assimilation methods. Journal of Geophysical Research--Atmospheres, 117: D17113. DOI: 10.1029/2012jd017684. |
| Qian T, Dai A, Trenberth KE, et al., 2006. Simulation of global land surface conditions from 1948 to 2004. Part I: Forcing data and evaluations. Journal of Hydrometeorology, 7(5): 953-975. DOI: 10.1175/JHM540.1. |
| Sang Y, Wang D, Wu J, et al., 2011. Wavelet-based analysis on the complexity of hydrologic series data under multi-temporal scales. Entropy, 13(1): 195-210. DOI: 10.3390/e13010195. |
| Sheffield J, Goteti G, Wood EF, 2006. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. Journal of Climate, 19(13): 3088-3111. DOI: 10.1175/JCLI3790.1. |
| Syed TH, Famiglietti JS, Rodell M, et al., 2008. Analysis of terrestrial water storage changes from grace and gldas. Water Resource Research, 44(2): W02433. DOI: 10.1029/2006WR005779. |
| Tang M, 1985. The distribution of precipitation in mountain Qilian. Acta Geographica Sinica, 40(4): 323-332. |
| Torrence C, Compo GP, 1998. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society, 79(1): 61-78. DOI: 10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2. |
| Wang F, Wang L, Koike T, et al., 2011. Evaluation and application of a fine-resolution global data set in a semiarid mesoscale river basin with a distributed biosphere hydrological model. Journal of Geophysical Research-Atmospheres, 116: D21108. DOI: 10.1029/2011jd015990. |
| Wang H, Chen Y, Li W, et al., 2013. Runoff responses to climate change in arid region of northwestern China during 1960-2010. Chinese Geographical Science, 23(3): 286-300. DOI: 10.1007/s11769-013-0605-x. |
| Wang N, Zhang S, He J, et al., 2009. Tracing the major source area of the mountainous runoff generation of the Heihe River in northwest China using stable isotope technique. Chinese Science Bulletin, 54(16): 2751-2757. DOI: 10.1007/s11434-009-0505-8. |
| Wen X, Fang J, Diao M, et al., 2013. Artificial neural network modeling of dissolved oxygen in the Heihe River, Northwestern China. Environmental Monitoring and Assessment, 185(5): 4361-4371. DOI: 10.1007/s10661-012-2874-8. |
| Wu X, Yang M, Wu H, et al., 2013. Verifying and applying the TRMM TMPA in Heihe River Basin. Journal of Glaciology and Geocryology, 35(2): 310-319. |
| Yang K, Koike T, Kaihotsu I, et al., 2009. Validation of a dual-pass microwave land data assimilation system for estimating surface soil moisture in semiarid regions. Journal of Hydrometeorology, 10(3): 780-793. DOI: 10.1175/2008jhm1065.1. |
| Zhang J, Li D, 2004. Analysis on distribution character of rainfall over Qilian Mountain and Heihe valley. Plateau Meteorology, 23(1): 81-88. |
| Zhou L, Yang G, 2006. Ecological economic problems and development patterns of the arid inland river basin in northwest China. Ambio, 35: 316-318. DOI: 10.1579/06-S-193.1. |
| Zhu S, Wang Q, 1996. Temporal-spatial distributions and recent changes of precipitation in the northern slopes of the Qilian Mountains. Journal of Glaciology and Geocryology, 18(S1): 296-304. |
 2015, 7
2015, 7


